Un po’ di teoria
Sin dagli inizi, i chimici hanno usato diagrammi per agevolare la comprensione della struttura delle molecole. Ad esempio, la molecola del metano si può rappresentare in questo modo (fig. 1), da cui risulta che l’atomo di carbonio è legato a quattro atomi di idrogeno e che nessun atomo di idrogeno è legato con altri atomi di idrogeno.
Altri diagrammi possono fornire maggiormente il senso che la molecola del metano è tridimensionale, e danno anche informazioni più accurate, perché le etichette ci dicono ad esempio la lunghezza del legame o gli angoli tra i legami. Il disegno di fig. 2 è fatto in modo da mostrare la natura tetraedrica della molecola di metano, cosa difficile da vedere nel precedente diagramma.
Questo tipo di diagrammi si può considerare all’interno della struttura dei diagrammi geometrici chiamati grafi. La teoria dei grafi riguarda lo studio delle proprietà dei diagrammi che utilizzano punti e segmenti lineari. I punti sono chiamati vertici o nodi, collegati fra loro da archi o spigoli. I vertici sono in genere trattati come oggetti senza caratteristiche e indivisibili.
Un arco che ha due estremi coincidenti si dice cappio, mentre più archi che connettono gli stessi due estremi costituiscono un multiarco. Un grafo sprovvisto di cappi e di multiarchi si dice grafo semplice. In caso contrario si parla di multigrafo (fig. 3).
Un sottografo G’ è un grafo composto da un sottoinsieme dei nodi e degli archi di un grafo G più grande.
Un percorso di lunghezza n in G è dato da una sequenza di vertici v0, v1,..., vn (non necessariamente tutti distinti) e da una sequenza di archi che li collegano. I vertici v0 e vn si dicono estremi del percorso. Un percorso con gli archi a due a due distinti tra loro prende il nome di cammino. Un cammino chiuso (v0 = vn) si chiama circuito o ciclo. Un cammino in un grafo è detto hamiltoniano se esso tocca tutti i vertici del grafo una e una sola volta. Un cammino viene invece detto euleriano quando tocca tutti gli archi del multigrafo una e una volta sola.
Dato un grafo, due vertici che appartengono ad esso, v e u si dicono "connessi" se esiste un cammino con estremi v e u. Se tale cammino non esiste, v e u sono detti "sconnessi".
Quando questi diagrammi sono usati dai chimici, essi sono solitamente chiamati grafi molecolari o formule di struttura. Una formula di struttura del metano è rappresentata in figura 4. I vertici rappresentano gli atomi, etichettati in modo da indicare di che tipo sono, e gli archi rappresentano i legami formati tra gli atomi. In questo caso il diagramma non fornisce alcuna informazione metrica, e gli angoli tra i legami e la loro lunghezza non fanno parte dell’informazione fornita. Cosī, la teoria dei grafi è un tipo di geometria che non utilizza direttamente informazioni metriche.
Potrebbe sembrare che la figura 4 non rappresenti un gran progresso rispetto alla 1. In realtà i grafi permettono considerazioni e forniscono informazioni assai più vaste di quanto appaia a prima vista. Utilizzando la teoria matematica dei grafi si aprono molte nuove prospettive sulla chimica delle molecole, anche se le rappresentiamo attraverso diagrammi sul piano.
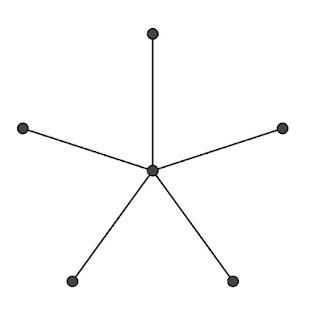
I chimici sanno che il grafo di figura 5 (un grafo a stella) non può essere il diagramma di struttura di un idrocarburo: il carbonio non può avere cinque legami. Ciò che regola questo tipo di diagrammi dal punto di vista di un chimico è che diversi tipi di atomi possono formare solo determinati tipi di legami con altri atomi. In pratica la possibilità di costruire grafi rappresentanti la struttura delle molecole è limitata dal concetto chimico di valenza. Gli esperti di teoria dei grafi rendono l’idea di legame tra atomi con il concetto di grado o valenza di un vertice di un grafo. Consideriamo ora la formula di struttura dell’etilene, in figura 6.
Questa è la versione secondo la teoria dei grafi della figura 5. Notate che, se si conta il numero degli archi per ogni vertice, ci sono due vertici in cui concorrono quattro archi e due che ne hanno uno solo. Se sommiamo questi numeri, otteniamo 4 + 4 + 1 + 1 + 1 + 1 = 12, che è il doppio del numero degli archi. Ciò è un fatto generale, dato che, se ogni singolo arco ha esattamente due estremità, la somma del numero di archi concorrenti in ciascun vertice darà sempre la metà del numero dei vertici.
Consideriamo il grafo di figura 8. Esso ha 6 vertici e 18 archi. Tuttavia, alcuni di questi archi uniscono un vertice a se stesso, formando un cappio, e per alcuni vertici c’è più di una coppia di spigoli che collega la stessa coppia di vertici. Quando il grafo presenta tali caratteristiche, con vertici uniti da più archi, essi sono detti a archi multipli.
In matematica c’è la “libertà” di definire i termini in modo tale da cogliere importanti idee applicative, come ad esempio la valenza in chimica. Si è così tentati di definire la valenza o grado dei vertici nella figura 8 come il numero di archi che concorrono in un vertice. Tuttavia, quando lo si fa, non è vero che la somma delle valenze dei vertici del grafo è uguale al doppio della somma del numero degli archi. I responsabili sono i cappi, che danno non uno, ma due estremità a un vertice. Tenendo ciò in considerazione, useremo la seguente definizione di valenza o grado di un vertice:
Dato un vertice v di un grafo G, il grado di un vertice è il numero di archi che concorrono in quel vertice.
Ciò significa che nella figura 8 abbiamo le seguenti valenze per i vertici:
valenza (v) = 4
valenza (w) = 6
valenza (x) = 6
valenza (y) = 5
valenza (u) = 6
valenza (z) = 9
Gli anelli blu contribuiscono per 2 alla valenza dei vertici in un cui concorrono, gli archi rossi (quelli multipli) contribuiscono per 1, come gli archi grigi. Notiamo che un vertice ha valenza dispari, mentre altri hanno valenza pari.
Se sommiamo i numeri 4 + 6 + 6 + 5 + 6 + 9 otteniamo 36, che è il doppio del numero degli archi, che di conseguenza sono 18. Possiamo quindi enunciare il seguente teorema:
Teorema:
Il grado o somma delle valenze di un grafo risulta uguale al doppio del numero degli archi.
Corollario:
Il numero di vertici di un grafo di valenza dispari è pari.
Dimostrazione: La somma di un numero dispari di numeri dispari è dispari, così per avere una somma pari per le valenze, bisogna avere un numero pari di vertici con valenza dispari.
La teoria dei grafi in chimica
L’importanza della teoria dei grafi in chimica incominciò a diventare evidente nel XIX secolo, grazie all’opera dei due matematici britannici, Arthur Cayley (1821-1895) e James Joseph Sylvester (1814 -1897).
Soprattutto il lavoro di Cayley fu pionieristico per l’uso di ciò che oggi chiamiamo grafi nella chimica, per cui dovette coniare anche una terminologia specifica. Egli utilizzò i termini plerogrammi e kenogrammi per i due tipi di grafi che si possono considerare quando si studiano gli idrocarburi con molecole lineari o ad albero (senza anelli). Il plerogramma mostra tutti gli atomi presenti, compresi gli idrogeni, mentre il kenogramma mostra solamente gli atomi di carbonio.
Nella figura 9 sono rappresentati il plerogramma (Pl1) e il kenogramma (Ke1) nel caso del 2,2,3,5-tetrametilesano: il kenogramma ha n e il plerogramma 3n + 2 vertici. Qui n = 10.
Una delle prime scoperte dei chimici fu che le molecole con lo stesso numero di atomi di carbonio e idrogeno (ad esempio) potevano presentare proprietà fisiche e chimiche diverse. Le molecole con le stesse proprietà chimiche, ma diverse proprietà fisiche sono dette isomeri l’una dell’altra. Quando rappresentiamo le molecole con strutture a grafo, gli isomeri danno luogo a strutture diverse. La teoria dei grafi fa parte della geometria combinatoria, nel senso che essa non si occupa delle proprietà metriche (area, angoli, distanze, ecc.), ma delle proprietá strutturali. Eppure, dai grafi si possono ottenere quantità di informazioni sorprendentemente grandi osservando le loro proprietá. Prendiamone in esame alcune. Consideriamo il grafo nella figura 10. Quali proprietà possiede?
I teorici dei grafi hanno coniato termini per descrivere come ci si muove su di essi da un vertice all’altro lungo gli archi. Per esempio, ci sono diversi percorsi dal vertice e al vertice i mostrato in figura, come ecbfglhi, ecflghi, oppure ecbglhi. Questi percorsi hanno lunghezze rispettivamente 7, 6 e 6, poiché tale è il numero degli archi attraversati. Ci sono tuttavia percorsi più corti da e a i, che utilizzano un minor numero di archi. Sia ecbghi sia ecflhi hanno lunghezza 5. Possiamo definire la distanza tra due vertici in un grafo connesso come la lunghezza del percorso più breve tra di essi. La distanza tra i vertici e e k è 4, mentre quella tra e e g è 3, essendoci due possibilità per percorrere questa distanza più breve: ecfg e ecbg. Si noti che questo diagramma può essere interpretato come quello di un idrocarburo, in quanto tutti i suoi vertici hanno valenza 1 oppure 4.
Alcuni grafi connessi hanno solo un percorso tra ogni coppia di vertici. Tali grafi non possono avere circuiti (cbgfc e fglf sono esempi di circuiti nel grafo sopra rappresentato). Dati due vertici in un circuito, ci sono due percorsi che li uniscono lungo le due parti che collegano i vertici. Un grafo senza circuiti si definisce ad albero (fig. 11), e gli alberi hanno molte utili proprietà, tra le quali il fatto che, tranne l’albero con un solo vertice, essi hanno almeno due vertici monovalenti. Un’altra elegante proprietà di un albero è questa:
Teorema 1:
Se T è un albero in cui il numero di vertici ė n, allora il numero di archi di T è n - 1.
Forse ancor più degno di nota è che anche l’inverso del teorema è vero:
Teorema 2:
Se T è un grafo connesso che possiede n vertici e n - 1 archi, allora il grafo T deve essere ad albero.
Uno dei risultati di Cayley fu mostrare che i grafi ad albero mostrano un ruolo particolarmente importante nella comprensione dei problemi di chimica matematica. Talvolta si conosce per ragioni chimiche il numero di atomi di idrogeno e carbonio che fanno parte di una serie di molecole. Ad esempio, gli alcani sono una famiglia di idrocarburi in cui, se ci sono n atomi di carbonio, ci sono 2n + 2 atomi di idrogeno, con la formula generale:
CnH2n+2
Che forma avranno i grafi di queste molecole? Utilizzando un po' di teoria dei grafi si può osservare che queste molecole devono avere una struttura ad albero.
Poiché le molecole chimiche sono connesse, ciò vuol dire che un alcano ha un totale di n (carbonio) + 2n + 2 (idrogeno) atomi. Quindi nel grafo di una tale molecola si hanno 3n + 2 vertici. Tuttavia, il carbonio è tetravalente, mentre l’idrogeno è monovalente. Per questo motivo ne risulta che 4n (4 volte il numero degli atomi di carbonio) + 1(2n +2) (1 volta il numero degli atomi di idrogeno) = 4n + 2n +2 = 2(3n+1), che è due volte il numero dei legami nella molecola. Così il numero di archi (legami) nel grafo della molecola è 3n +1. Dato che il numero dei vertici 3n + 2 supera di uno il numero degli archi, 3n +1, possiamo concludere per il teorema 2 che i diagrammi per gli alcani sono sempre ad albero.
Possiamo considerare i grafi per comprendere meglio un aspetto utile si chimici. Dato un grafo connesso, dove sono i vertici che sono “al centro” o “in mezzo” al grafo? Domande di questo tipo furono poste dal matematico francese Camille Jordan (1838 - 1922).
Il primo approccio per spiegare che cosa s'intende per “centro” di un grafo è utilizzare queste definizioni:
L’eccentricità di un vertice n è la massima distanza di n da qualsiasi altro vertice.
Un vertice n di un grafo (connesso) è detto centrale se l’eccentricità di n è la più piccola possibile.
Ricordiamo che la distanza tra due vertici è la lunghezza del cammino più breve tra di essi. Nella figura 10, per esempio, i vertici d, e, i e j hanno eccentricità 5, i vertici a, c e h hanno eccentricità 4 e i vertici b, f, g e l hanno eccentricità 3. Sono questi ultimi i vertici centrali.
Il centro C di un grafo connesso connesso G consiste di tutti i suoi vertici centrali assieme agli archi che li uniscono. Talvolta si dice che il centro di un grafo connesso è il sottografo di G “indotto” o generato” dai vertici centrali. Nella figura 10 il centro è costituito dai 4 vertici b, f, g e l e dai 5 archi bf, bg, fl, gl, e fg.
Bisogna osservare che considerazioni del genere talvolta non sono di grande utilità, poiché ogni vertice di un grafo può essere centrale e perciò il centro del grafo è il grafo stesso. Un esempio è il cubo tridimensionale (fig. 12, in due rappresentazioni isomorfiche), in cui tutti i vertici hanno eccentricità 3.
Ad ogni modo, ciò che ci interessa è che per grafi ad albero con almeno 3 vertici non tutti i vertici possono essere centrali.
Teorema:
Se T è un grafo ad albero, allora il centro di T è o un singolo vertice o una coppia di vertici con l’arco che li unisce.
Nella figura 13 si vede l’esempio di un grafo ad albero (che rappresenta la molecola di un idrocarburo: quale?) il cui centro è costituito dall’arco disegnato in rosso con i vertici che unisce.
Un’altra proprietà notevole dei grafi ad albero e dei loro centri è che se si ha un grafo T con almeno 3 vertici e si rimuovono i vertici monovalenti, il grafo ad albero che si ottiene ha lo stesso centro di quello originale. Ad esempio, il grafo di figura 14 conserva il suo centro (il vertice in rosso) anche dopo che sono stati “potati” i vertici monovalenti.
Quando Cayley iniziò a occuparsi degli isomeri degli idrocarburi ad albero, dovette decidere quale modello di grafo adottare per la molecola. Gli idrocarburi con molecola ad albero hanno vertici tetravalenti e monovalenti e abbiamo appena visto che il centro di tale molecola è lo stesso per il grafo in cui sono tolti i vertici monovalenti. Cayley doveva scegliere tra il plerogramma, con inclusi i vertici monovalenti, e il kenogramma, che invece rappresenta solo gli atomi di carbonio. Il butano C4H10 è costituito da due isomeri, l’ n-butano e l’isobutano, i cui kerogrammi sono rappresentati nella figura 15.
Un’altra proprietà notevole dei grafi ad albero e dei loro centri è che se si ha un grafo T con almeno 3 vertici e si rimuovono i vertici monovalenti, il grafo ad albero che si ottiene ha lo stesso centro di quello originale. Ad esempio, il grafo di figura 14 conserva il suo centro (il vertice in rosso) anche dopo che sono stati “potati” i vertici monovalenti.
Quando Cayley iniziò a occuparsi degli isomeri degli idrocarburi ad albero, dovette decidere quale modello di grafo adottare per la molecola. Gli idrocarburi con molecola ad albero hanno vertici tetravalenti e monovalenti e abbiamo appena visto che il centro di tale molecola è lo stesso per il grafo in cui sono tolti i vertici monovalenti. Cayley doveva scegliere tra il plerogramma, con inclusi i vertici monovalenti, e il kenogramma, che invece rappresenta solo gli atomi di carbonio. Il butano C4H10 è costituito da due isomeri, l’ n-butano e l’isobutano, i cui kerogrammi sono rappresentati nella figura 15.
Cui corrispondono alle seguenti formule di struttura:
L’indice di Wiener
Molto tempo dopo che Cayley, Sylvester e Jordan avevano mostrato che le loro idee sulla teoria dei grafi non si applicavano al solo campo matematico, un chimico, Harry Wiener, diede nuovo impulso alla teoria dei grafi in chimica creando, nel 1947, un invariante di un grafo che prende il nome Indice di Wiener. Si tratta del più antico indice topologico legato alla struttura molecolare. Dopo il suo successo, molti altri indici topologici di grafi chimici, basati sul dato della matrice grafica del grafo, sono stati sviluppati.
La domanda per i chimici e i matematici interessati alla chimica è se l’informazione riguardo al grafo di una molecola consente di “predire”, anche solo approssimativamente, le proprietà chimiche o fisiche della stessa. La risposta ottenuta dalle evidenze sperimentali è che ciò è possibile.
L’idea di Wiener era di guardare alle distanze tra i vertici del grafo che rappresenta la molecola. Se la molecola corrisponde a un albero, quale grafo ne rappresenta meglio le proprietà? Wiener scelse originariamente per il suo Indice il grafo degli idrocarburi che indica solo gli atomi di carbonio. Ad esempio, calcoliamo l’Indice di Wiener per i due grafi rappresentati in figura 15. La molecola dell’n-butano possiede tre coppie di vertici a distanza 1 l’uno dall’altro. due coppie a distanza 2 e 1 coppia a distanza 3, così il suo Indice vale:
3 x 1 + 2 x 2 + 1 x 3 = 10
La molecola dell’isobutano possiede 3 coppie di vertici a distanza 1 l’uno dall’altro (i le tre coppie vertice esterno-centro) e 3 coppie a distanza 2 (le coppie da vertice esterno a vertice esterno). Pertanto il suo Indice vale:
3 x 1 + 3 x 2 = 9
Questi valori sono esempi di formule di casi speciali dell’Indice di Wiener. Esso vale (n3 - n)/6 per n vertici in linea come nel caso dell’n-butano e (n - 1)2 per n vertici disposti a stella come nel caso dell’isobutano. Così, anche se queste due molecole hanno la stessa formula chimica e lo stesso numero di legami carbonio-carbonio e carbonio-idrogeno, le loro strutture diverse originano due Indici di Wiener diversi.
Wiener dimostrò che i valori del suo indice sono legati da vicino ai punti di ebollizione delle molecole degli alcani. Opere più recenti sulle relazioni quantitative tra struttura e attività hanno evidenziato che l’indice è correlato con altre quantità, come i parametri del punto critico, la densità, la tensione superficiale e la viscosità della fase liquida, e la superficie di van der Waals della molecola.
Mentre l’indice di Wiener per grafi non isomorfi è diverso, ci sono anche casi in cui grafi non isomorfi hanno lo stesso indice. Ciò non è sorprendente. I matematici da tanto tempo stanno tentando di trovare un modo semplice di dire che due grafi sono isomorfi oppure no. Nessun indice di tale tipo è finora stato trovato né sembra probabile che lo sia. Infatti, il “Problema dell’isomorfismo dei grafi”, vale a dire sapere se e in quanto tempo si può dimostrare che due grafici con n vertici sono isomorfi, è in computer science una questione tuttora irrisolta.
Riferimento Principale:















Invece di "Mentre l’indice di Wiener per grafi non isomorfi è diverso" dovrebbe essere "Mentre l'indice di Wiener per grafi isomorfi è uguale".
RispondiEliminaEsiste un legame tra quanto sopra esposto e i gradi libertà di una molecola ?
RispondiEliminacaino
«Si è così tentati di definire la valenza o grado dei vertici nella figura 8 come il numero di archi che concorrono in un vertice. Tuttavia ... Tenendo ciò in considerazione, useremo la seguente definizione di valenza o grado di un vertice: Dato un vertice v di un grafo G, il grado di un vertice è il numero di archi che concorrono in quel vertice.»
RispondiEliminaNon mi è chiara la differenza... E inoltre, in entrambi i casi, x e w dovrebbero avere valenza 5 (ci sono 5 archi diversi incidenti a x, anche se ne escono 6 “mozziconi”), e y 4, no?
I cappi sono archi singoli che concorrono 2 volte al grado di un vertice.
EliminaGrazie, MFB, ma allora forse va formulata meglio la definizione di grado (menzionando una sorta di molteplicità degli archi o qualcosa del genere, perché il “numero di archi” conta una volta ogni arco, che sia un cappio o no).
RispondiEliminaHai ragione. Finiti gli scrutini lo faccio...
Elimina