Il profeta della quarta dimensione

Vero figlio della sua epoca, nella quale le geometrie non euclidee e le dimensioni plurime dello spazio alimentavano gli entusiasmi di matematici e fisici e le speculazioni di spiritisti e teosofi, sospeso tra Lobachevsky e Madame Blavatsky, il matematico inglese Charles Howard Hinton fu, nella seconda metà dell’Ottocento, il profeta della quarta dimensione. Non lo fu però in quanto matematico (o lo fu solo in modo relativo), ma come autore di alcuni romanzi–saggio che, se non lo hanno collocato nel novero dei seguaci di Pitagora e Archimede, gli hanno almeno garantito un posticino tra gli anticipatori della science–fiction.

Nato nel 1853 da una famiglia borghese di idee illuminate e filantropiche, Howard Hinton si era nutrito di una cultura eterogenea e di una mentalità aperta e liberale, decisamente in anticipo sui suoi tempi. Aveva compiuto i suoi studi di matematica e si era diplomato a Oxford nel 1877. Nello stesso anno sposò Mary Boole, la figlia del celebre matematico e logico George Boole, con la quale trascorse qualche anno di serena vita famigliare, divisa tra gli studi e l’insegnamento di scienze alla Uppingham School di Rutland, nell’Inghilterra centrale. In quegli anni, tra il 1880 e il 1886, attraverso il collega Howard Candler (futuro proprietario per un biennio della Coca–Cola), aveva conosciuto Edwin Abbott Abbott, autore nel 1882 del celebre racconto scientifico e satirico Flatland. Nel 1886 si era laureato, sempre a Oxford.

Chi lo conobbe lo descrive di mente lucida e arguta, capace di spingersi avanti a immaginare nuovi orizzonti concettuali. In un articolo del 1880, intitolato What Is the Fourth Dimension? (Che cos’è la quarta dimensione?), suggerì che punti in movimento in uno spazio tridimensionale posso essere immaginati come successive sezioni di un oggetto quadridimensionale che attraversa le tre dimensioni, un’idea che anticipava il concetto di linea di universo di Minkowski (la generalizzazione in uno spazio a quattro dimensioni del concetto di traiettoria di un corpo) e quello di quarta dimensione assimilabile al tempo presente nella teoria della relatività di Einstein, nonostante l'articolo fosse soprattutto incentrato sulle possibilità di una quarta dimensione spaziale. Nello stesso periodo aveva cominciato la stesura dei materiali per un primo libro di narrativa scientifica, Scientific romances, che sarebbe uscito a fascicoli separati tra il 1884 e il 1886. Tra questi racconti, che comprendevano anche l’articolo del 1880 oltre a A Picture of Our Universe, Many Dimensions e An Unfinished Communication, c’era A Plane world, la sua risposta a Flatland di Abbott, simile nell’impostazione ma, a detta dell’autore, scritto con intenti diversi: Abbott avrebbe usato “l’impianto [del racconto] per collocare la sua satira e le sue lezioni. Ma noi vogliamo in primo luogo conoscere i fatti fisici”.

Già in queste prime opere è evidente l’interesse preponderante, quasi maniacale, di Hinton per il concetto di quarta dimensione, da lui ritenuta una qualità dell’universo meritevole di attenzione e ricerca. Ancor di più, egli credeva che lo sforzo compiuto per impadronirsi di quest’idea potesse avere un potenziale effetto innovativo su tutto l’insieme delle convinzioni individuali e collettive. Insomma, la quarta dimensione era per Hinton uno strumento per l’evoluzione totale del pensiero umano.

Intanto incominciava a maturare nella sua mente, sempre più influenzata dal pensiero teosofico, un’avversione per ogni tipo di trattazione formale, matematica, della geometria e della fisica. A suo parere, il sistema della “dimostrazione” dei teoremi era un metodo troppo freddo e meccanico per cogliere davvero la realtà profonda delle cose. Preferiva una “appercezione intuitiva”, condotta ricorrendo a espedienti di vario tipo, alla portata di tutti, come l’analogia e l’immedesimazione. Coerente con queste idee, e con lo scopo di diffonderle, egli rifiutò di utilizzare il tradizionale saggio scientifico o divulgativo, preferendo la forma del racconto scientifico, più appetibile dal lettore comune al quale si indirizzava. La sua esperienza di insegnante lo portò a rifuggire da formule matematiche e da argomentazioni troppo complesse, preferendo una esposizione per analogia, che egli utilizzò in modo massiccio e spesso incontrollato.

A questo punto il vostro cronista deve intervenire per sostenere che le scelte espositive e didattiche di Hinton, pur opinabili se utilizzate in modo esclusivo, non erano completamente campate per aria. Certamente tutti hanno qualche idea del significato di parole come punto, linea, angolo, poiché capita d'impiegarle quotidianamente. Eppure, leggendo gli Elementi di Euclide, che costituiscono la base della geometria classica, le definizioni giungono improvvise e inquietanti: "un punto è ciò che non ha parti", "la linea è lunghezza senza larghezza". Chiunque avrebbe ragione di chiedersi se frasi come queste possono essere comprese, perché ci si trova ai limiti delle possibilità del linguaggio, alle soglie del non-senso. Volendo insegnare a un bambino il significato di queste parole, non si cercherà certamente di introdurre il concetto di punto o di linea tentando di dire che cosa sono. Non si dirà che il punto è "ciò che non ha parti", invitandolo poi a disegnare qualcosa privo di parti, oppure non si dirà che la linea è "lunghezza senza larghezza", chiedendogli di disegnare qualcosa che è lungo, ma non è largo. Probabilmente si mostrerà un punto o una linea su un foglio di carta, impiegando nello stesso tempo la parola corrispondente e dicendo "è così". Poi, dopo aver ripetuto in vari modi queste operazioni, s'inviterà il bambino a disegnare una linea o un punto, esprimendo approvazione o disapprovazione fino a che si potrà essere ragionevolmente certi che il concetto è stato compreso. Ciò che si sarà messo in opera, l'insieme di pratiche nelle quali le parole sono state integrate da gesti, comportamenti, raccomandazioni, rimproveri, è un insegnamento ostensivo (ostendere significa "mostrare"), nel quale è evitata la definizione verbale.

Ora, come fare in modo che un concetto come la quarta dimensione, così lontano dalla nostra esperienza quotidiana, possa essere afferrato da chi è completamente digiuno di matematica? Il concetto, al di fuori delle relazioni simboliche e formalizzate della matematica, è indicibile, non può essere espresso con le parole del linguaggio naturale, perché tocca il fondamento stesso del linguaggio, è ai suoi limiti (che sono poi i nostri). La scelta del filosofo austriaco Ludwig Wittgenstein nel 1929 sarà quella di separare ciò "che si dice", da "ciò che si mostra", l'indicibile. Mentre "ciò che si dice" riguarda il campo della scienza, che tratta i fenomeni descrivibili attraverso il linguaggio naturale o simbolico e formalizzato, "ciò che si mostra" riguarda invece il fatto che non può essere espresso della descrizione, il fatto del linguaggio stesso. Wittgenstein decise che “Su ciò di cui non si può parlare si deve tacere”. In matematica si procede allo stesso modo, basando ogni sistema formale su un certo numero di assiomi e postulati non dimostrati e dati per veri. La scelta di Hinton fu invece quella di procedere per analogia e per metafora, avvicinando il concetto di quarta dimensione attraverso una serie di passi che, nelle sue intenzioni, avrebbero consentito di raggiungere, di portar fuori (metafora deriva da meta-phoréin, "portar fuori"), l'altrimenti indicibile. In realtà è dubbia l’efficacia dei ragionamenti e delle analogie scelti da Hinton, al punto che ci fu chi lo accusò di aver portato alla pazzia alcuni dei suoi lettori, ma il suo tentativo non va bollato come stravagante: egli non era un fou littéraire.

Hinton sosteneva che non ci sono prove contrarie all'esistenza di un universo nel quale le dimensioni dello spazio si susseguono l'una all'altra. Il fatto che noi non siamo in grado di concepirne intuitivamente più delle tre abituali, diceva, è il frutto solo della nostra limitatezza. Il punto di partenza del suo ragionamento era immaginare uno spazio fatto di due sole dimensioni, senza nessuna altezza, proprio come aveva illustrato Abbott in Flatland. Su un mondo piatto di quel genere, immaginari esseri intelligenti potrebbero muoversi in due soli sensi: in avanti-indietro e in alto-basso. Non si renderebbero conto del vincolo che li lega alla superficie sulla quale stanno attaccati e, per loro, l'universo consisterebbe di quest'unica condizione di esistenza sul piano. Non conoscendo altro, non potrebbero concepire una realtà come la nostra, che possiede anche una direzione perpendicolare al piano delle altre due. Non potrebbero interagirvi se non per quella porzione che i due universi hanno in comune, cioè il loro piano stesso. Se, ad esempio, noi, che viviamo nello spazio tridimensionale, appoggiassimo su quel piano un oggetto cubico, gli abitanti di Flatlandia lo percepirebbero come un quadrato; lo scoprirebbero girandoci attorno, dato che non possono sollevarsi in alto a gettare uno sguardo d'insieme alla figura. E se spingessimo quel cubo attraverso il piano, magari inclinandolo un po', creeremmo stupore tra quegli esseri bidimensionali in grado di scorgere solo una figura piana che cambia forma e dimensioni, diventando irregolare, poi grande, piccola e infine puntiforme, fino a scomparire del tutto. Ai loro occhi sarebbe un portento inspiegabile. Analogamente, non saprebbero comprendere la nostra possibilità di osservare l'interno di una figura piana chiusa, di collocarvi dentro qualcosa senza rompere i lati del perimetro, e così via. Inoltre noi, dalla nostra prospettiva superiore, potremmo accorgerci che oggetti visti separati dagli esseri bidimensionali di Flatland possono essere uniti nella terza dimensione. Appoggiando due delle nostre dita sul loro piano–universo, i residenti di Flatlandia vedrebbero due figure circolari distinte: noi però sapremmo che fanno parte della stessa struttura, la mano, distesa nella direzione dello spazio a loro invisibile.

Tutto questo, sosteneva Hinton, vale per estensione anche per noi e per i nostri rapporti con una realtà a quattro dimensioni, invisibile di solito ai nostri occhi. Come gli abitanti di Flatlandia non si rendono conto di essere vincolati a un piano, così noi potremmo essere soggetti a un vincolo tridimensionale, del quale siamo tanto pervasi da non percepirne l'esistenza.

Gli oggetti attorno a noi, inoltre, potrebbero trovare la loro realtà più piena proprio nella quarta dimensione. Come su Flatlandia un cubo poggiato sul piano dà un'intersezione a forma di figura piana, così un oggetto quadridimensionale inserito nel nostro spazio a tre dimensioni potrebbe produrre un'intersezione a forma di solido. Al limite, potrebbe darsi che tutto quanto vediamo sia la proiezione nel nostro universo di qualcosa che sta 'altrove'. E oggetti separati, come gli stessi individui umani, potrebbero in verità essere uniti. In questa maniera Hinton apriva le porte a una strana filosofia idealista che rifletteva alcuni dei suoi valori umanitari, ma che poteva alimentare, come infatti accadde, le speculazioni degli allora diffusissimi occultisti.

Tornando alla biografia di Hinton, bisogna segnalare che anche la sua vita privata andò incontro a un drammatico cambiamento, una rivoluzione per i costumi dell’epoca. Stanco nel menage familiare, nel 1885 si era sposato una seconda volta, con una tale Maude Wheldon, che gli avrebbe poi dato due gemelli. Il fatto è che Hinton non si era minimamente preoccupato di divorziare dalla prima moglie! L’anticonformismo del nostro non piacque affatto alla società vittoriana e all’autorità costituita che la rappresentava: denunciato, venne arrestato, processato, condannato e privato d’un colpo di donna, lavoro e denaro. Scontò un solo giorno di prigione, ma iniziò una serie di vagabondaggi per il mondo che alla fine lo condussero negli Stati Uniti. Qui incominciò a frequentare i circoli intellettuali e politici liberal, tenne conferenze e si fece apprezzare per la sua preparazione matematica. Nel 1893 lo troviamo Istruttore di Matematica all’Università di Princeton.

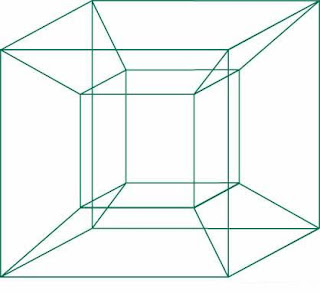
Nel 1888, poco dopo aver lasciato l’Inghilterra, aveva dato alle stampe presso il suo editore londinese A New Era of Thought, opera profondamente rimaneggiata in fase redazionale su sua esplicita richiesta, perché egli “doveva partire per un impegno importante che l’avrebbe tenuto lontano a lungo, forse per sempre”. In realtà era già iniziato il suo volontario esilio. Il libro è suddiviso in due parti. La prima è una collezione piuttosto disorganica di saggi matematici e filosofici sulla quarta dimensione. Essi trattano del pensiero quadrimensionale e delle implicazioni filosofiche e religiose di tale nuova acquisizione del pensiero. Nella seconda parte Hinton sviluppa una serie di cubi colorati, che servono da metodo per sviluppare una percezione quadridimensionale sulla base di un progressivo allenamento. Viene anche mostrato come visualizzare un ipercubo, o tesseratto, termine coniato dallo stesso Hinton, cioè l’equivalente del cubo nelle quattro dimensioni, con l’osservazione di un certo numero di sue sezioni tridimensionali.

I lettori di A New Era of Tbought potevano avere, su richiesta all'editore, un set di cubi, ciascuno colorato in maniera diversa dagli altri e ciascuno con un proprio nome. Seguendo le istruzioni contenute nel libro, chi aspirava a una visione “superiore” doveva svolgere una serie di esercizi sempre più complicati. Da principio bisognava semplicemente creare blocchi di cubi impilati uno sull'altro, e spostarli sottosopra o ruotarli; poi le operazioni divenivano sempre più difficili e andavano compiute per lo più mentalmente. Il neofita doveva imparare a memorizzare i singoli costituenti del blocco (ricordarne bene colore, nome, posizione) e riuscire a immaginarne lo spostamento nello spazio, curando che al movimento di ogni cubo si spostasse in maniera congruente tutto il complesso degli altri. Ciò si poteva fare, sosteneva Hinton, se si cercava di “immedesimarsi” con quei cubi, di identificarsi con essi, di sentirli quasi espansioni del proprio corpo e addirittura centro della propria coscienza.

Giunto in America, Hinton si astenne dallo scrivere per un lungo periodo, ma trovò ugualmente il modo di far parlare di sé. Nel 1897 progettò una specie di mitragliatrice che sparava palle da baseball, da utilizzare per gli allineamenti della squadra universitaria di Princeton. L’invenzione causò molti incidenti con feriti, ed è probabile che il suo insuccesso fu la causa principale delle dimissioni dall’ateneo quello stesso anno. La macchina era tuttavia versatile, regolabile in alzo, direzione e potenza e, attraverso un particolare congegno di gomma, poteva anche lanciare palle “tagliate” con traiettoria curvilinea. Opportunamente migliorata, fu utilizzata dalla squadra dell’università del Minnesota, dove Hinton si trasferì fino al 1900 per poi trovare posto all’Osservatorio Navale di Washington.

Nel 1902 riprese le sue pubblicazioni sulla quarta dimensione, con il saggio matematico–filosofico The Recognition of the Fourth Dimension, seguito più tardi dal volume The Fourth Dimension (1904), summa finale del suo pensiero, in cui riprendeva il metodo dei cubi colorati per visualizzare la quarta dimensione. Approfondendo il discorso su come rappresentarsi questo mondo, Hinton utilizzò in questo volume immagini decisamente anticipatorie. Parlò infatti di un “movimento quadridimensionale nel settore delle piccole particelle di materia che produrrebbe un movimento analogo all’elettricità” e sostenne che “un vortice che abbia per asse una superficie produce un’immagine geometrica di un circuito chiuso”, anticipando in qualche modo la singolare conformazione della quarta dimensione immaginata dallo svedese Oscar Klein, per il quale essa sarebbe in realtà arrotolata su se stessa e ridotta in proporzioni infinitesime, frammentata in un numero infiniti vortici più piccoli, dalle dimensioni miliardi di volte inferiori a quelle delle particelle subatomiche.

Pubblicò infine An Episode of Flatland (1907), in cui tornava a parlare della percezione delle tre dimensioni da parte degli immaginari abitanti di un mondo bidimensionale. Passato a lavorare per l’Ufficio Brevetti americano, morì improvvisamente il 30 aprile 1907 per un’emorragia cerebrale mentre sorseggiava una bevanda durante un ricevimento di un gruppo proto–femminista della Società di Ricerca Filantropica di Washington. Aveva solo 54 anni, di sicuro vissuti assai intensamente.

Ebbe pochi e distratti necrologi sulla stampa del tempo, sintomo del velo di oblio che sarebbe caduto su di lui. Solo Jorge Luis Borges avrebbe per un po’ sollevato quella cortina di silenzio, citandolo tra vari pensatori bizzarri nel bellissimo racconto Il miracolo segreto (qui lo si può leggere per intero), contenuto nella raccolta Finzioni (Einaudi), e curando nel 1978 la traduzione dei Scientific romances nel volumetto Racconti scientifici per la collana Biblioteca di Babele di Franco Maria Ricci. Negli stessi anni, il canadese Harold Coxeter, uno dei più grandi geometri del XX secolo, battezzò politopo di Hinton un poliedro quadridimensionale descritto da Hinton nel suo volume del 1904.