Il solitario Barricelli e la nascita degli organismi numerici

 

Il MANIAC (acronimo di Mathematical Analyzer, Numerical Integrator And Computer), la cui architettura fu progettata quasi esclusivamente da John von Neumann agli inizi degli anni Cinquanta, era il più potente “cervello elettronico” dell’epoca e fu installato presso l’IAS (Institute for Advanced Study) di Princeton, nel New Jersey. Finanziato quasi interamente con fondi delle forze armate, serviva principalmente per eseguire i complessi calcoli che portarono alla costruzione della bomba termonucleare all’idrogeno. Il suo nome, scherzoso e non ufficiale, faceva il verso a quello dell’ENIAC, che lo aveva preceduto dal 1946, sempre con scopi principalmente militari (e per le previsioni meteorologiche). C'erano cinque kilobyte di memoria totale archiviati nella macchina. Un’inezia per gli standard odierni, ma allora era un arsenale.

Maniac è il nome anche della bella e documentata biografia romanzata di John von Neumann e storia dell’evoluzione del suo calcolatore elettronico, scritta dal cileno Benjamín Labatut (Adelphi, 2023). Di sicuro Labatut ha giocato con il significato della parola che, in inglese come in italiano, indica una persona con problemi mentali, un pazzo. E il libro abbonda di figure di persone geniali e un po’ folli, a cominciare dallo stesso matematico di origine ungherese. Ma von Neumann non è il solo. A metà circa di Maniac compare e scompare nel giro di due capitoli non consecutivi l’enigmatica e affascinante figura di Nils Aall Barricelli.

Nella finzione letteraria ne parla la testimonianza di Julian Bigelow, l’ingegnere informatico che fu il braccio destro di Von Neumann nella progettazione e nella realizzazione della macchina. Il capitolo si intitola proprio “Un vero scienziato pazzo”.

Appena il MANIAC cominciò a funzionare Johnny chiamò a lavorarci un vero scienziato pazzo. 

Nils Aall Barricelli. 

Mezzo norvegese e mezzo italiano. 

Totalmente folle.

A Johnny era venuta un'ossessione per la biologia, e quest'uomo lasciò nel suo ufficio un bigliettino scritto a mano. 

“Interessato a condurre una serie di esperimenti numerici allo scopo di verificare la possibilità che un'evoluzione simile a quella degli organismi viventi abbia luogo in un universo creato artificialmente”. 

Con accluse specifiche e alcune pubblicazioni accademiche. 

Johnny mi chiese cosa ne pensavo. 

Non aspettò la mia risposta. 

L'indomani gli accordò libero accesso. 

Gli disse che poteva far girare qualunque simulazione volesse. 

Una volta terminati i calcoli per la bomba, ovviamente.

Barricelli era nato a Roma il 24 gennaio 1912 da padre italiano e madre norvegese. Secondo Richard Goodman, un microbiologo che fece amicizia con il matematico negli anni '60, Barricelli affermava di aver inventato il calcolo infinitesimale prima del suo decimo compleanno. Quando il ragazzo mostrò i calcoli a suo padre, apprese che Newton e Leibniz lo avevano preceduto di un paio di secoli. Mentre era studente all'Università di Roma, Barricelli studiò matematica e fisica con Enrico Fermi. Un paio d'anni dopo la laurea nel 1936, emigrò in Norvegia con la madre recentemente divorziata e la sorella minore.

Mentre infuriava la Seconda guerra mondiale, Barricelli studiava. Nonostante avesse presentato una tesi di 500 pagine sull'analisi statistica delle variazioni climatiche nel 1946, Barricelli non completò mai il suo dottorato di ricerca. La commissione di tesi gli ordinò di ridurre l’articolo a un decimo delle dimensioni, altrimenti non avrebbe accettato il lavoro. Invece di capitolare, Barricelli rinunciò alla laurea.

Barricelli iniziò a modellare i fenomeni biologici su carta, ma i suoi calcoli erano lenti e limitati. Fece domanda per studiare negli Stati Uniti come borsista Fulbright, dove avrebbe potuto lavorare con la macchina IAS. Come scrisse nella sua richiesta di borsa di studio originale nel 1951, cercò di “effettuare esperimenti numerici per mezzo di grandi macchine calcolatrici”, al fine di chiarire, attraverso la matematica, “i primi stadi dell’evoluzione di una specie”. Desiderava anche socializzare con grandi menti: “comunicare con statistici e teorici dell’evoluzione americani”. Al momento della presentazione della domanda era un assistente di 39 anni presso l'Università di Oslo.

Sebbene il programma inizialmente lo respinse a causa di un problema di visto, all'inizio del 1953 Barricelli arrivò all’Institute for Advanced Study come membro in visita. "Spero che troverete il signor Baricelli [sic] una persona interessante con cui parlare", scrisse Ragnar Frisch, un collega di Barricelli che più tardi avrebbe vinto il primo Premio Nobel per l'economia, in una lettera a von Neumann. “Non è sempre molto sistematico nella sua esposizione”, continuava Frisch, “ma ha idee interessanti”. Comunque, non è vero che “fu chiamato”, ma fu presentato con ottime credenziali.

Le sue idee erano deliranti. 

Voleva imitare all'interno del MANIAC l’evoluzione della vita.

“Il primo linguaggio e la prima tecnologia sulla Terra non furono creati da esseri umani. Furono creati da molecole primordiali quasi quattro miliardi di anni fa. Sto pensando alla possibilità che un processo evolutivo potenzialmente in grado di condurre a risultati analoghi si possa avviare nella memoria di un calcolatore”.

Credeva nella simbiogenesi. 

Una teoria estremamente controversa opposta al darwinismo. 

Spiega la complessità degli organismi viventi attraverso le associazioni simbiotiche anziché mediante la selezione naturale dell'ereditarietà. 

Una fusione tra forme più semplici.

L'ipotesi simbiogenetica fu articolata per la prima volta dal naturalista russo Konstantin Merezhkovsky nel 1905. Egli era già a conoscenza del lavoro svolto dal botanico tedesco Andreas Schimper, che, avendo osservato nel 1883 come la divisione dei cloroplasti nelle piante verdi ricordasse quella dei cianobatteri, aveva proposto che le piante verdi derivino dall'unione simbiotica di due organismi. Successivamente, nel 1920, Ivan Wallin estese l'idea di un'origine endosimbiontica anche ai mitocondri. Ma tutte queste ipotesi furono inizialmente tralasciate o confutate. Analisi più dettagliate di cianobatteri e cloroplasti, effettuate grazie al microscopio elettronico, e la scoperta che i plastidi e i mitocondri contengono un proprio DNA (che fu riconosciuto come il materiale ereditario degli organismi) portarono a una rivalutazione dei fatti negli anni Sessanta.

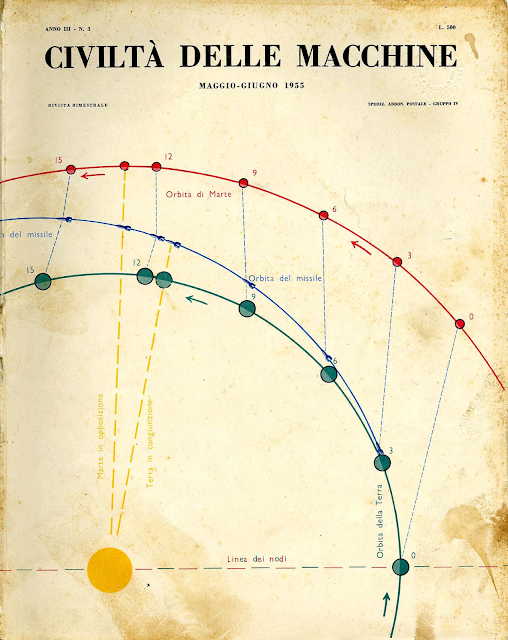
Come avrebbe scritto lo stesso Barricelli in un lungo articolo riguardante il suo lavoro su Civiltà delle macchine di Leonardo Sinisgalli (1955: a. 3, mag., fasc. 3, pp. 27-33), “Un'ipotesi ardita fu avanzata nel 1924 da Kozo-Polyansky quando già si cominciava a sapere qualche cosa di queste analogie. L'ipotesi di Kozo-Poliansky è che tutti i geni ed anche diverse altre molecole della cellula che sono dotate di potere autocatalitico discendono da altrettanti virus od organismi di natura simile ai virus che per simbiosi un po’ per volta si sono associati al resto della cellula. Secondo questa teoria, che Kozo-Polyansky chiama teoria della “simbiogenesi“, il processo di evoluzione che ha permesso la formazione della cellula fu iniziato da una simbiosi tra alcuni organismi di natura simile ai virus. A questi poi col tempo si sarebbero associati nuovi simbionti della stessa natura ed in numero sempre crescente, ed il processo di evoluzione così iniziato avrebbe reso possibile la formazione dei vari organi della cellula”. 

Sul registro del computer di Barricelli presso l’Institute for Advanced Study, in caratteri scritti a mano a matita datati 3 marzo 1953, c’è il titolo “Problema di simbiogenesi”.

La teoria della simbiogenesi nella sua moderna accezione fu esposta e diffusa per la prima volta nel 1975 da Lynn Margulis, che la ufficializzò nel 1981 nel libro Symbiosis in Cell Evolution (La simbiosi nell'evoluzione cellulare); nel libro viene spiegato come le cellule eucariotiche si siano originate come comunità di entità interagenti tra loro, tra cui ad esempio spirochete endosimbiontiche che svilupparono flagelli e ciglia eucariotici, ma la biologa andrebbe, con più ragione, ricordata per la sua opera di divulgatrice. Infatti, alle spalle dell’opera di Lynn Margulis c’è una lunga storia di idee, alle quali è molto debitrice (e stranamente non cita l’articolo di Kozo-Polyansky che Barricelli conosceva bene).

Attualmente la simbiogenesi è largamente accettata e supportata da prove scientifiche. Nei primi tempi venne accettata molto lentamente tra i biologi, ma grazie al largo numero di prove portate a sostegno nei 30 anni seguenti, è utilizzata su un numero sempre maggiore di sistemi biologici. Oggi è l'unica spiegazione plausibile esistente per l'evoluzione e la discontinuità esistente tra procarioti ed eucarioti.

Disseminò di numeri casuali la memoria del MANIAC.  

Introdusse regole per governare il loro comportamento. 

È così che li faceva “evolvere”. 

La sua ipotesi era che avrebbero cominciato a mostrare le stesse caratteristiche dei geni.

(...)

Ognuno degli organismi di Barricelli era una stringa di numeri. 

Entravano in contatto si fondevano mutavano morivano o procreavano. 

Potevano instaurare una simbiosi per diventare più complessi. 

Potevano regredire a forme piü semplici. 

Trasformarsi in predatori. In parassiti.

Barricelli codificò i suoi organismi numerici sulla macchina IAS per dimostrare la sua tesi. Scrisse che "È molto facile fabbricare o semplicemente definire entità con la capacità di riprodursi, ad esempio, nel regno dell'aritmetica".

Ma qual era il metodo che utilizzava? Lo spiega nell’articolo su Civiltà delle macchine:

“Per esempio, possiamo usare come elementi alcuni numeri scritti sulla prima linea di un foglio a quadretti - vedi fig. 1 dove i numeri negativi sono sottolineati - e scegliere ad arbitrio una regola di riproduzione di questi numeri.

In fig. 1 si è usata la seguente: in una unità di tempo (generazione) un numero positivo m si riproduce m caselle a destra ed un numero negativo n si riproduce n caselle a sinistra. Il risultato che si ottiene dalla prima riga seguendo questa regola di riproduzione è scritto nella seconda riga. Applicando la stessa regola di riproduzione sulla seconda riga si ottiene la terza riga, e così via. Naturalmente per continuare bisognerà fissare delle regole per fissare ciò che dovrà avvenire quando due numeri capitano nella stessa casella. Ma di ciò si parlerà più avanti.

L’altra facoltà essenziale per una evoluzione darwiniana, la capacità di subire cambiamenti ereditari, non è così diffusa come la capacità di riprodursi, ma si conoscono elementi in cui la detta capacità esiste (...) Artificialmente non vi è alcuna difficoltà a definire elementi che oltre alla facoltà di riprodursi hanno anche la facoltà di subire cambiamenti ereditari. Negli elementi numerici sopra definiti possiamo per esempio stabilire delle regole di mutazione approfittando dei casi in cui due numeri capitano nella stessa casella. Il numero da collocare nella detta casella potrà risultare diverso da entrambi e rappresenterà in tal caso una mutazione. (...)

In questo modo si ha una classe di elementi numerici capaci di riprodursi è di subire mutazioni. Le condizioni per un processo di evoluzione in base ai principi di Darwin sarebbero presenti. I numeri, che hanno maggiore probabilità di sopravvivere nell’ambiente creato dalle regole che abbiamo scelto, sopravviveranno. Gli altri verranno man mano eliminati. Si avrà un processo di adattamento all’ambiente, un processo di evoluzione darwiniana”.

Poi, per indurre processi di evoluzione, cambiava le regole: “Per mettere alla prova la teoria della simbiosi dei geni possiamo ricorrere ancora una volta all’impiego di elementi numerici. Basterà modificare le regole della riproduzione impiegate in maniera tale da favorire qualche forma di associazione utilitaria (simbiosi) tra elementi numerici diversi. Così si potrà vedere se è vero che associando elementi con le proprietà fondamentali precedentemente descritte si possa iniziare un processo di evoluzione che si svolga in base allo stesso meccanismo che regola l’evoluzione biologica. Per favorire l’associazione utilitaria (simbiosi) possiamo apportare alle regole di riproduzione adottate delle modifiche per (...) rendere possibile la riproduzione di un elemento numerico solo quando ne sono presenti degli altri da esso differenti. In tal modo si rende necessaria l'associazione utilitaria (simbiosi) di elementi numerici diversi onde rendere possibile la riproduzione. Alle suddette regole di riproduzione si possono poi associare delle regole di mutazione a piacere, per es. sfruttando i casi in cui due numeri cadono nella stessa casella”.

E così via, fino alla prova di compilare la prima riga (generazione) di soli 1 e -1 e caselle vuote (0) estraendoli a sorte in modo casuale con il lancio di due monete.

Il bello è che, all’inizio, faceva tutto con penna e fogli quadrettati. Solo successivamente ebbe la possibilità di ricorrere alla schede perforate del computer.

All'interno del dispositivo, Barricelli programmò mondi costantemente mutabili, ciascuno con file di 512 "geni", rappresentati da numeri interi relativi. Mentre il computer attraversava centinaia e migliaia di generazioni (il massimo fu 5.400) emergevano raggruppamenti persistenti di geni, che Barricelli considerava organismi. Il trucco consisteva nel modificare le leggi della natura create dall’uomo - “norme”, come le chiamava lui - che governavano l’universo e le sue entità. Doveva mantenere questi ecosistemi sull’orlo del disordine e della stasi. Troppo caos e le sue creature si sarebbero trasformate in un caos disorganizzato; troppo poco e si sarebbero omogeneizzate. Il punto nel mezzo, tuttavia, sosteneva processi realistici.

L’azione di equilibrio di Barricelli non era sempre facile. Le sue prime prove furono piene di parassiti: geni numerici primitivi, spesso singoli, invasero lo spazio e divorarono i loro vicini. In genere, era in grado di assistere solo a un paio di cambiamenti ereditari, o al massimo a una manciata, prima che il mondo si distruggesse. Per creare processi evolutivi duraturi, aveva bisogno di ostacolare la capacità di questi parassiti di riprodursi rapidamente. Quando tornò all'Istituto nel 1954 per iniziare una seconda serie di esperimenti, Barricelli apportò alcuni cambiamenti cruciali. Innanzitutto, limitò la proliferazione dei parassiti a una volta per generazione. Questo vincolo consentiva ai suoi organismi numerici un più ampio margine di manovra per superare il problema. In secondo luogo, iniziò a impiegare norme diverse per le diverse sezioni dei suoi universi. Ciò costringeva i suoi organismi numerici ad adattarsi sempre.

Anche negli universi precedenti, Barricelli si rese conto che la mutazione e la selezione naturale da sole non erano sufficienti a spiegare la genesi delle specie. In effetti, la maggior parte delle singole mutazioni erano dannose. Scrisse che “La maggior parte delle nuove varietà che hanno mostrato la capacità di espandersi sono il risultato di fenomeni di incrocio e non di mutazioni, sebbene le mutazioni (soprattutto quelle dannose) siano state molto più frequenti dei cambiamenti ereditari mediante incrocio negli esperimenti condotti".

Quando un organismo diventava perfettamente adatto ad un ambiente, la più piccola variazione non faceva altro che indebolirlo. In tali casi, furono necessarie altre modificazioni, effettuate mediante una fecondazione incrociata, per dare all'organismo numerico una qualche possibilità di miglioramento. Ciò indicava a Barricelli che le simbiosi, l’incrocio genetico e “una forma primitiva di riproduzione sessuale” erano essenziali per l’emergere della vita.

Barricelli programmò alcuni dei primi algoritmi informatici che assomigliano ai processi della vita reale: una suddivisione di ciò che oggi chiamiamo “vita artificiale”, che cerca di simulare i sistemi viventi nei computer. Barricelli lanciò una sfida coraggiosa al modello darwiniano standard di evoluzione per competizione, dimostrando che gli organismi si sono evoluti anche per simbiosi e cooperazione.

In effetti, i progetti di Barricelli hanno anticipato molte attuali vie di ricerca, compresi gli automi cellulari, programmi per computer che coinvolgono griglie di numeri abbinate a regole locali che possono produrre comportamenti complicati e imprevedibili. I suoi modelli hanno una sorprendente somiglianza con gli automi cellulari unidimensionali (reticoli realistici di schemi numerici) proposti da Stanislaw Ulam e, manco a dirlo, da von Neumann, e studiati da Stephen Wolfram.

Barricelli vedeva i suoi organismi informatici come un modello di vita, su questo pianeta e su qualsiasi altro. "La questione se un tipo di simbioorganismo si sviluppi nella memoria di un computer digitale mentre un altro tipo si sviluppi in un laboratorio chimico o mediante un processo naturale su qualche pianeta o satellite non aggiunge nulla di fondamentale a questa differenza", scrisse. Un mese dopo che Barricelli aveva iniziato i suoi esperimenti sulla macchina IAS, Crick e Watson annunciarono la forma del DNA come una doppia elica. Ma conoscere la forma della vita biologica non ha intaccato la convinzione di Barricelli di aver catturato i meccanismi della vita su un computer. Lasciamo che Watson e Crick definiscano il DNA una doppia elica. Barricelli li chiamava “numeri a forma di molecola”.

Ogni due cicli prendeva un campione dalla memoria del MANIAC e lo stampava.

Rigogliosi paesaggi matematici simili a giganteschi quadri espressionisti astratti.

L'elettroencefalogramma di un folle. 

Fissava un punto e gridava Perfetto! quando gli organismi si erano scambiati dei "geni" per creare un simbionte. 

Scandaloso! quando diventavano parassiti.

Gli esperimenti di Barricelli avevano anche un lato estetico. Insolitamente per l’epoca, convertì gli 1 e gli 0 digitali della memoria del computer in immagini pittoriche per evidenziare i suoi organismi numerici Quelle immagini, e le idee alla loro base, avrebbero influenzato gli animatori computerizzati nelle generazioni a venire.

Barricelli non si è limitato a creare un universo di organismi numerici, ha convertito i suoi organismi in immagini. I conteggi computerizzati di 1 e 0 si sarebbero poi auto-organizzati in griglie visive di squisita varietà e consistenza.

Barricelli era convinto che i numeri potessero cominciare a sviluppare una vita propria.

Sono l'inizio di una qualche forma di vita aliena o semplicemente modelli della vita? No, non sono modelli. Sono una particolare categoria di strutture autoreplicanti, già definite!

“Ma deve essere ben chiaro che il compito delle nostre ricerche non è stato quello di indagare come si siano svolte le prime fasi dell’evoluzione biologica. Il nostro compito è invece di indagare se processi di evoluzione in base agli stessi principi che, come si suppone, regolano l’evoluzione biologica sono possibili e come si svolgerebbero inizialmente partendo da elementi numerici o di qualsiasi natura anche se completamente diversi dai virus e dai geni, purché capaci di riprodursi, di mutare ereditariamente e di associarsi in organizzazioni (simbioorganismi) che offrono un vantaggio selettivo”.

(...)

“Processi di evoluzione secondo i principi dell’evoluzione biologica e i cui i fenomeni di incrocio (o riproduzione sessuale) hanno una parte preponderante, possono essere realizzati con molti tipi di elementi capaci di riprodursi, mutare ed associarsi in simbioorganismi. Non si tratta quindi di un fenomeno particolare caratteristico per un determinati tipo di elementi, come ad esempio le molecole degli acidi desossiribonucleici (virus e geni), ma di un fenomeno statistico generale che interessa molti tipi di elementi con le suddette proprietà”.

(...)

“La possibilità di produrre processi di evoluzione insieme agli stessi principi che regolano l’evoluzione biologica, ma partendo da elementi autoriproduttivi di natura qualsiasi, solleva la questione se gli organismi numerici ed eventualmente altri organismi che possono essere sviluppati in simili processi di evoluzione siano da considerarsi come organismi viventi. Teoricamente siffatti organismi, se sviluppati in universi di dimensioni sufficienti e in condizioni adatte, potrebbero avere le stesse e forse anche maggiori possibilità di evoluzione e varietà di forme. Che si voglia o no riconoscerli come organismi viventi, ciò potrà in definitiva essere una questione di definizione. Volendo scegliere una definizione molto comprensiva si potrebbe considerare come vivente ogni organismo capace di riprodursi e di subire cambiamenti ereditari. Con questa definizione sarebbero viventi non solo i virus e i geni, ma anche gli organismi numerici e gli elementi numerici che li compongono”.

(...)

“Ma anche volendo considerare come viventi soltanto i simbioorganismi di natura, diciamo così, albuminica, non bisogna credere che tutti questi organismi debbano necessariamente rassomigliare alle forme di vita che conosciamo sulla Terra né che la Terra debba essere necessariamente l’ambiente migliore per lo sviluppo di siffatte forme di vita”.

Ma alla fine i suoi esperimenti fallirono. 

Sebbene io abbia creato una classe di numeri capaci di riprodursi e di subire mutamenti ereditari, l’evoluzione numerica non va molto lontano e non ha prodotto in nessun caso un livello di fitness sufficiente a mettere la specie al riparo dalla totale distruzione e ad assicurare un processo evolutivo illimitato come quello che ha avuto luogo sulla Terra e che ha portato a organismi sempre più avanzati. Manca qualcosa che permetta di spiegare la formazione di organi e di facoltà complesse come quelle degli organismi viventi. Per quante mutazioni facciamo, i numeri restano sempre numeri. Non diventeranno mai organismi viventi! 

Appunti presi in preda alla disperazione.

Ciarlatano/visionario? 

Probabilmente entrambe le cose. 

Molto in anticipo sul suo tempo. 

Troppo.

Le sue entità numeriche evolvevano in un universo digitale vuoto nel corso dei pochi cicli di calcolo lasciati liberi dalla bomba all’idrogeno. 

Chissà cosa sarebbe riuscito a ottenere con più cicli a disposizione. 

Ma svanirono senza lasciare tracce. 

Molte delle sue idee furono riscoperte in seguito da altri ricercatori che non erano a conoscenza del suo lavoro.

Fu Johnny a seppellirlo? Forse. 

Fra loro accadde qualcosa. Litigarono di brutto. 

Nessuno dei due ha mai riconosciuto il lavoro dell'altro. 

Nemmeno una parola nei loro scritti. Ho controllato. 

Come se non si fossero mai conosciuti. 

Johnny è ancora riverito come il padre della vita artificiale. 

Mentre l'altro pazzo non lo ricorda nessuno. 

Un giorno di punto in bianco gli fu negato l'accesso al MANIAC. 

Non lo vedemmo mai più.

Ciò che ha sepolto Barricelli nell'oscurità è qualcosa di misterioso. Essere intransigente nelle sue opinioni e non un giocatore di squadra, senza dubbio ha portato all’isolamento di Barricelli dal mainstream accademico. Ma è probabile che Barricelli e l’indomabile von Neumann non andassero più d’accordo.

In un successivo capitolo che Labatut attribuisce alla testimonianza di Barricelli, forse è contenuta la verità sul suo allontanamento da Princeton e dal MANIAC:

“Non sono pazzo. Non sono mai stato pazzo. Non sono folle, anche se molte mi hanno definito così. In tutti questi anni travagliati, questi anni infernali passati a lavorare lontano da tutti, ignorato, vilipeso e invisibile, non ho perso la testa, non ho lasciato che lo sconforto mi conducesse alla follia e mi precipitasse nel delirio. (...) Sono un uomo di scienza. Un sostenitore del potere della verità, un avversario dell'ignoranza e un nemico naturale del nichilismo e dell’incommensurabile abisso della disperazione, perché mi sono votato al futuro. (...) Ma io ho visto qualcosa che mi ha fatto capire che esistono lande selvagge irriducibili alla sola logica, qualcosa che si fa beffe dei venerati principi che gli scienziati hanno tanto a cuore, quel loro cuore debole è pavido - ho visto la vita digitale. Non è in arrivo, è qui. Le creature che ho immaginato si stanno evolvendo più in fretta di quanto potrebbe fare un qualunque sistema biologico. Tanto belle quanto inevitabili. (...) Perciò ho sopportato l’umiliazione di divenire un oggetto di scherno. Uno zimbello. Un esempio negativo, deriso da uomini inferiori sospinti in alto dalle volgari gerarchie del mondo. (...) Ormai è la rabbia a sostenermi (...) Perché è stato a causa della rabbia, del puro rancore cieco che una volta - una volta sola - sono andato vicino a perdere la testa. Ira e sdegno, stizza e odio nei confronti della gazza ladra, di quel demonio sorridente, John von Neumann.

Ha rubato le mie idee! Ha sabotato e usurpato i miei esperimenti, quei numeri scrupolosamente ibridati tra loro che già traboccavano di promesse di vita, e quando non è riuscito a piegarli ai suoi obiettivi li ha distorti e travisati. (...) Usando la sua influenza, ha seppellito la mia ricerca e anche il mio nome, prima negandomi l’accesso al suo calcolatore (il MANIAC, nome quanto mai appropriato), poi evitando deliberatamente qualunque riferimento diretto al mio lavoro in uno dei suoi libri, proprio quello che - per motivi che mi sfuggono - viene considerato da tutti come il compendio definitivo sugli automi e gli organismi digitali. (...) Non ho nemmeno potuto far ricorso: quel bastardo è morto prima di completare il suo libro. (...) Da allora sono rimasto impotente a guardare mentre altri sfruttavano e mietevano un campo che ero stato io il primo a concimare, seminare e far germogliare. (...) Ed è stato allora, quando mi trovavo a un passo dalla scoperta, quando la mia terra promessa cominciava a profilarsi all’orizzonte, che von Neumann ha preso a interessarsi al mio progetto.

All’inizio ne era affascinato quanto me. Arrivava all’istituto nel cuore della notte - l’unico momento in cui mi era concesso lavorare - e mi tempestava di domande molto insistenti. Da quel che sceglieva di chiedere si capiva la qualità del suo pensiero (...) ed ebbi l’opportunità di scrutare dentro la sua testa. Mi chiese se avessi sentito parlare delle macchine di Turing con oracolo. Col tempo sono giunto a considerare quella semplice domanda come un test (...) Turing anelava a qualcosa di diverso [dai calcolatori moderni], una macchina capace di guardare oltre la logica e comportarsi in modo più simile agli esseri umani, che sono dotati non solo di intelligenza, ma anche di intuito. (...)”

Nella sua accezione più ampia, un oracolo può essere considerato come una serie di procedure di decisione in grado di superare i limiti di una Macchina di Turing, In pratica, l’accesso all’oracolo renderebbe una macchina ibrida capace di affrontare classi di problemi che nessun sistema algoritmico può risolvere. Un altro campo in cui gli oracoli hanno mostrato una funzione teorica è nella classificazione dei problemi “trattabili” o “intrattabili”, risolvibili cioè in tempo polinomiale o esponenziale in relazione alla dimensione n del problema. Ovviamente, il potere di calcolo di una macchina di Turing con oracolo è conseguenza diretta delle caratteristiche di decidibilità del linguaggio oracolo. Una macchina di Turing con oracolo è tale se, di fronte a un problema computazionale incalcolabile, almeno in certo tempo, in cui è necessaria una scelta (sì o no), tira a indovinare, esattamente come facciamo noi.

“Non dimenticherò mai quel momento. (...) Ero arrivato all’istituto a mezzanotte e stavo scendendo le scale che conducevano al MANIAC, quando (...) mi accorsi subito, con mio estremo sconcerto, che il MANIAC stava lavorando a pieno regime, e che von Neumann stava facendo girare il mio codice. Il mio codice!” (...) Lui mi assecondò è non parve risentirsi per il mio tono, ma quando notai che aveva ottimizzato diverse subroutine e introdotto importanti cambiamenti nei miei successivi cicli computazionali, alterando le mie istruzioni in modi che non riuscivo a comprendere, persi il controllo. Mi sentii a tal punto tradito che lo spinsi via è balzai in avanti per interrompere il processo prima che fosse troppo tardi. (...)

Non riesco a ricordare cosa dissi a quel mostro per allontanarlo dal mio esperimento, ma ricordo con assoluta chiarezza che lui reagì in modo sorprendentemente pacato. (...) Fece orecchie da mercante alle mie lamentele e si limitò ad andarsene senza proferire parola, e senza scusarsi per quel che aveva fatto. Né mai si sarebbe scusato in futuro. Quella fu l’ultima volta in cui ci parlammo, e capii subito che i miei giorni col MANIAC erano contati”.

Insomma, mentre Barricelli voleva ricreare la vita in un ambiente digitale, von Neumann voleva creare l’intelligenza artificiale. In più era molto più potente, e non certo uno stinco di santo.

Barricelli morì a Oslo nel 1993, solo e dimenticato.

Il sordido Merezhkovsky

 

Le storie che si raccontano sugli scienziati sono spesso eroiche. La figura la cui idea rivoluzionaria viene rifiutata, dimenticata e poi confermata è un classico di tale narrazione. A mio parere, uno dei principali difetti della divulgazione in rete delle conquiste della scienza è quello di presentare molti scienziati e scienziate come individui eccezionali, spesso in lotta contro ambienti sociali e intellettuali ostili, talvolta illuminati da improvvisi lampi di genio e da considerare come nuovi maestri di saggezza, di cui si ricordano frasi celebri come meme o si citano aneddoti edificanti. Va bene, alcuni lo sono stati, ma in realtà gli uomini e le donne di scienza sono esseri umani come tutti gli altri, con i loro pregi e difetti, che talvolta possono essere addirittura dei crimini.

Lasciamo perdere le frodi accademiche, oramai tanto diffuse da sembrare banali, in cui ambizione, sete di profitto e di carriera, hanno portato e portano tuttora alcuni a plagiare le scoperte di altri, a truccare o aggiustare i dati sperimentali, a pubblicare su riviste a pagamento di dubbia affidabilità, addirittura a minacciare fisicamente o a denunciare chi li sbugiarda (per fortuna la comunità scientifica ha sviluppato per sua natura un cospicuo apparato di anticorpi e di metodi per scoprire le truffe, che prima o poi vengono smascherate).

Lasciamo anche perdere i casi più clamorosi e citati in cui, in particolari momenti della storia, mossi dal nazionalismo e dall’ideologia, con scopi fatti addirittura passare per “umanitari”, alcuni singoli o gruppi di scienziati hanno progettato e propugnato armi di distruzione di massa per finire in fretta una guerra (i gas nelle trincee, la bomba atomica) o addirittura evitarne altre (alcuni tra gli “alieni ungheresi” emigrati negli USA furono tentati dall’idea di bombardare preventivamente l’Unione Sovietica con le bombe A prima che i russi potessero averle anch’essi, per evitare una Terza guerra mondiale).

No, in questo caso parlo di crimini più comuni e odiosi.

Prendiamo il caso di Konstantin Merezhkovsky (1855-1921), considerato il “padre” della simbiogenesi (termine da lui coniato). Nei primi decenni del ventesimo secolo, suggerì che gli organelli cellulari come i mitocondri e i cloroplasti si fossero originati dalla simbiosi di organismi più semplici simili ai batteri. Presentò questa teoria nel 1910, nel suo lavoro “La teoria dei due plasmi come base della simbiogenesi, un nuovo studio sulle origini degli organismi”, sebbene i fondamenti dell'idea fossero già apparsi nel 1905 nel precedente articolo, “La natura e le origini dei cromatofori nel regno vegetale”. Le sue idee furono a lungo respinte e considerate eccentriche. Eppure, i suoi articoli a lungo dimenticati, ridicolizzati o emarginati, hanno in seguito ricevuto consensi in tutto il mondo. Eppure, eppure, questo geniale naturalista fu anche una spia zarista, un proto-nazista antisemita e un pedofilo seriale.

Nato nella famiglia di un alto funzionario imperiale, Konstantin Sergeevic Merezhkovsky (Константи́н Серге́евич Мережко́вский, poi traslitteratelo come più vi piace), ricevette una buona educazione. Il padre, Sergei Ivanovich, prestò servizio sotto gli imperatori Nicola I e Alessandro II nell'ufficio del dipartimento di corte. La madre era la figlia del direttore dell'ufficio del capo della polizia di San Pietroburgo. La famiglia contava cinque fratelli e tre sorelle, di cui uno, Dmitrij Sergeevic, diventò poeta simbolista e scrittore di romanzi impregnati di religiosità tipicamente russa.

Nel 1869 Konstantin entrò alla Facoltà di Giurisprudenza, poiché il padre voleva che suo figlio maggiore continuasse le tradizioni familiari e diventasse un funzionario, ma nel 1875 fece domanda all'Università Imperiale di San Pietroburgo per il dipartimento di scienze della natura della Facoltà di Fisica e Matematica. Mentre era ancora studente, sotto la guida dello zoologo degli invertebrati Nikolai Petrovich Wagner, iniziò a condurre studi scientifici (principalmente zoologici): si interessò alle diatomee e pubblicò i suoi primi lavori. Conseguì il diploma universitario il 20 novembre 1880.

Dopo la laurea fu mandato all'estero per due anni, dove studiò antropologia, zoologia e in parte botanica a Berlino, Parigi e Lipsia, oltre che alla stazione di biologia marina di Napoli. Al ritorno dall'estero, nel 1883 discusse la sua tesi "Materiali per la conoscenza dei pigmenti animali" e tenne lezioni di zoologia all'Università di San Pietroburgo (1884) e ai corsi superiori femminili. Nel 1880-1886 fu collaboratore di Wagner, e poi suo assistente. Le principali ricerche di questo periodo riguardavano i celenterati, gli idrozoi e le spugne.

Nel 1883 sposò Olga Petrovna Sultanova. Nel 1886 emigrò improvvisamente dalla Russia per motivi inspiegabili, forse collegati ad atti di violenza sessuale su minori per i quali fu alla fine perseguito penalmente. La famiglia si stabilì in Crimea, dove Konstantin trovò lavoro come botanico studiando le varietà di uva; creò anche una consistente collezione di diatomee del Mar Nero.

Il periodo di Crimea (1886-1898) fu segnato da studi speciali sulle diatomee del Mar Nero e del Mar d'Azov, nel 1897 lavorò alla stazione di Sebastopoli, poi andò alla stazione russa di Villefranche-sur-Mer presso Nizza, dove studiò le alghe. In questo periodo furono redatte le sue principali opere sulle diatomee. Contemporaneamente pubblicò articoli sulla viticoltura; nel 1898 gli fu commissionato uno studio fondamentale con illustrazioni, “Ampelografia [studio dei vitigni] della Crimea”. Nel 1898 lasciò la moglie e il giovane figlio in Crimea ed emigrò improvvisamente in America, dove prese il nome di William Adler.

Merezhkovsky rimase in America per 4 anni (1898-1902); lavorò all'Università di Berkeley vicino a San Francisco e visse per qualche tempo a Los Angeles sotto pseudonimo. Studiò le alghe, scrisse “Studi sull'endocromo delle diatomee”, pubblicò una serie di lavori che descrivevano nuovi taxa. Durante la sua permanenza negli Stati Uniti, scrisse Il paradiso terrestre, o sogno di una notte d'inverno, una favola ambientata nel ventisettesimo secolo: essenzialmente un’utopia fascista-eugenetica, con la riproduzione di una nuova razza umana secondo la sua forma ideale pedofila e l'utilizzo di schiavi asiatici e africani.

Nel 1902 tornò in Russia. Il 18 febbraio 1902 prese il posto di curatore del museo zoologico dell'Università di Kazan. Nel 1903 discusse la sua tesi sul tema "Sulla morfologia delle diatomee" e conseguì un master in botanica, dove sviluppò il suo nuovo interesse per i licheni. Il 14 gennaio 1904 Merezhkovsky fu nominato assistente professore nel dipartimento di botanica. Il 14 ottobre 1906 fu nominato professore straordinario ad interim presso l'Università Imperiale di Kazan. Il 17 gennaio 1907 fu confermato dottore in botanica e dal 1° gennaio 1908 divenne professore ordinario.

La duplice natura dei licheni come funghi e alghe, segnalata per la prima volta dal botanico svizzero Simon Schwendener nel 1867, aveva portato diversi biologi a considerare il ruolo della simbiosi nell'evoluzione. I licheni mostrano come nuovi organismi possano essere sintetizzati da due diversi tipi di organismi che vivono in intima associazione. Herbert Spencer aveva utilizzato la simbiosi dei licheni come microcosmo della sua visione super-organismica della vita. Lo vedeva come un “accordo comunista” basato su una divisione del lavoro tra pianta e animale. Ma le interpretazioni del rapporto tra alghe e funghi variavano, poiché i botanici impiegavano una varietà di metafore antropomorfe: Schwendener vedeva il lichene in termini di schiavitù da parte di un padrone fungino sulle alghe catturate, Johannes Reinke interpretava il rapporto come un consorzio.

Il famoso biologo tedesco Anton de Bary coniò il termine simbiosi nel 1879 come parola neutra semplicemente per indicare la convivenza di due o più organismi con nomi diversi, per abbracciare un continuum di relazioni dal parassitismo al mutualismo. Il termine symbiotismus era stato utilizzato l’anno precedente da Albert Bernard Frank, ricordato oggi soprattutto per i suoi studi pionieristici sulla simbiosi tra funghi e radici di piante da lui denominata “micorriza”. A partire dal 1880, furono trovate prove di alghe che vivevano all'interno dei protozoi e nel tessuto delle spugne, dell'idra e di alcuni vermi. Anche la simbiosi di batteri che fissano l'azoto nei noduli radicali delle leguminose è un fenomeno diffuso.

Quando tali esempi di simbiosi furono considerati alla luce di nuove prove citologiche della continuità fisica dei cloroplasti, portarono molti ricercatori a suggerire che varie parti della cellula (nucleo, citoplasma, cloroplasti, mitocondri e centrioli) si fossero evolute come simbionti. Che i cloroplasti potessero essere sorti come organismi simbiotici indipendenti era stato menzionato da molti biologi negli anni 1880 e 1890, tra cui l'ex studente di de Bary Andreas Schimper, che aveva notato che i cloroplasti delle cellule vegetali somigliavano ai cianobatteri. Merezhkovsky ricordava che l’idea gli era venuta “in modo del tutto spontaneo” dopo aver letto il classico articolo di Schimper del 1885. Schimper aveva anche suggerito che i cloroplasti potrebbero essersi formati per simbiosi nel suo famoso articolo del 1883 in cui coniò il termine “cloroplasto”.

Merezhkovsky sosteneva che gli organelli cellulari, il nucleo e i cloroplasti sono i discendenti di batteri che si sono evoluti in una simbiosi intracellulare con le amebe. Le idee di Merezhkovsky, a lungo rifiutate, diedero però il via una corrente sotterranea che percorse tutto il Novecento, finché sfociò nella moderna teoria della simbiogenesi sviluppata e resa popolare negli anni Settanta dall’americana Lynn Margulis, e ora ampiamente accettata nella visione darwinista come una forma di “evoluzione parallela”. La visione moderna è che si siano verificati due eventi endosimbiotici, uno con l’incorporazione di batteri che divennero i mitocondri di tutti gli eucarioti, e un altro subito dopo, nella linea che portò alle piante, per formare i cloroplasti.

Verso la fine del secolo, Merezhkovsky costituì un considerevole erbario di licheni, contenente oltre 2000 esemplari raccolti dalla Russia, dall'Austria e dal Mediterraneo. La collezione è conservata all'Università di Kazan.

Come molti studenti russi della fine del XIX secolo, Merezhkovsky iniziò ad essere a favore della rivoluzione. Ma finì per diventare un collaboratore della polizia segreta dello zar. Fu anche uno degli organizzatori di un'organizzazione nazionalista e antisemita di Kazan: il "Dipartimento di Kazan dell'Unione del popolo russo", un'organizzazione sostenuta dallo zar, ed era un mediatore segreto per il Ministero degli affari interni. In qualità di "professore di destra", come veniva chiamato, il suo compito era quello di cercare e riferire su tutte le circostanze pericolose e sospette e di sradicare gli ebrei e gli altri "traditori". Molti dei suoi colleghi furono allontanati dopo le sue denunce segrete e persino pubbliche al giornale di Kazan. Infatti, al famoso biologo, ittiologo e geografo fisico Lev Simonovic Berg (1876-1950), fondatore della limnologia in Russia, fu impedito di ottenere una cattedra all’Università di Kazan dopo le denunce pubbliche di Merezhkovsky. Berg era ebreo e Merezhkovsky lo odiava. Nel frattempo, continuò a fare scienza, fino a quando scoppiò lo scandalo.

Il 12 aprile 1914 presso il Dipartimento di Giustizia di San Pietroburgo fu aperto il procedimento penale numero 1303. (Fu chiuso il 22 febbraio 1917 e nel 1931 l'archivio fu distrutto per ordine della Direzione archivistica centrale). Un procedimento penale fu aperto anche a Kazan il 28 aprile da un investigatore del tribunale distrettuale della città. Il ministro della Pubblica Istruzione destituì Merezhkovsky dall'incarico di professore ordinario di botanica all'Università di Kazan e lo mise solo a disposizione. Merezhkovsky rimase ufficialmente in quella posizione fino al febbraio 1917.

Merezhkovsky fu accusato di pedofilia (di aver violentato almeno 26 ragazzine), e fuggì un’altra volta all'estero. Ne seguì uno scandalo di portata nazionale. Casi più vecchi rivelarono che era fuggito da San Pietroburgo nel 1886, poi dalla Crimea nel 1898, per paura di essere perseguito per stupro di giovani ragazze (non è escluso che fosse avvertito in precedenza dai suoi protettori politici). Sembra che anche in California fosse stato sospettato di almeno un episodio di violenza sessuale.

Merezhkovsky era fuggito in Francia nel 1914 dove rimase per gran parte della guerra: Nizza, Mentone e Parigi. Nel febbraio 1918 si rifugiò in Svizzera dove rimase per il resto della sua vita. Viveva molto modestamente grazie al reddito risparmiato, in una stanza dell'Hôtel des Familles a Ginevra. Fu lì, due settimane prima della fine della guerra, il 25 ottobre 1918, che tenne la sua ultima relazione su quello che considerava “il lavoro della sua vita”. Questa presentazione fu la base del suo lungo articolo, La plante considérée comme un complexe symbiotique, pubblicato due anni dopo nel "Bulletin de la Société des Sciences Naturelles de l’Ouest de la France". Merezhkovsky era amareggiato, malato e stanco. Come lamentava, da quando aveva annunciato la sua teoria sulla natura simbiotica dei cloroplasti nel 1905, “aveva fatto pochi progressi”; spesso veniva “completamente ignorato”. Aveva intenzione di scrivere un libro sull'argomento, ma altri lavori lo ostacolarono e poi, durante la lotta politica in Russia prima della guerra, era diventato troppo debole per scriverlo; “alla fine la guerra, la rivoluzione..." Così, osservava, "è solo oggi, alla vigilia di lasciare questo triste mondo, che ho deciso di sviluppare un po' più in dettaglio le mie idee per consolidare e ampliare la base su cui poggiano” . Merezhkovsky riferiva di aver scritto a più di cinquanta scienziati, editori e istituzioni (tra cui la Carnegie Institution) chiedendo loro di pubblicare l'opera, e spiegando loro che essendo privo di ogni risorsa non gli restava molto da vivere.

Il suo ultimo scritto, pubblicato a Ginevra, fu l'opera filosofica cosmogonica “Il ritmo universale come base di un nuovo concetto dell'universo” (1920), dove combinava il suo antisemitismo, l'eugenetica e un afflato spiritualista con l'idea che fosse "un salvatore dell'umanità". In esso prefigurava con approvazione la campagna di sterminio nazista contro gli ebrei europei.

A Ginevra cadde gravemente depresso, rimase senza soldi e il 9 gennaio 1921 fu trovato morto nella sua camera d'albergo dell'Hotel des Families, legato al letto con una maschera alimentata con un gas asfissiante da un contenitore metallico. Sembra che il suo suicidio fosse direttamente collegato alle sue convinzioni utopiche pedofile così come alla sua opinione che stava diventando troppo vecchio e malato per continuare la sua carriera di abusi sulle minorenni. Lasciò un biglietto scritto in latino, che poi andò perduto: "Troppo vecchio per lavorare e troppo malato per vivere" furono le ultime parole.

La matematica (e la scienza) in Arcadia

 

Sir Tom Stoppard (1937), è un drammaturgo, regista e scrittore britannico di origine cecoslovacca. Premio Oscar per la sceneggiatura di Shakespeare in Love, Stoppard è uno dei più apprezzati e prolifici autori britannici del secondo Novecento. Tra le sue opere è molto nota Rosencrantz e Guildenstern sono morti, uno spin-off scespiriano poi divenuta un film nel 1990 premiato con il Leone d'oro a Venezia. Nella sua commedia Arcadia (1993), le idee matematiche formano uno dei principali sottotemi dell'opera. In particolare, argomenti contemporanei come i frattali formano parte integrante della trama, e giocano un ruolo importante anche elementi come l’ultimo teorema di Fermat e la seconda Legge della Termodinamica. L'opera è ambientata in due periodi di tempo, l'inizio del XIX secolo e il presente, nella stessa stanza della tenuta di Sidley Park.

Una stanza davanti al giardino di una grande casa di campagna nel Derbyshire nell'aprile 1809. Oggi sarebbe chiamata una casa signorile. Il muro di fondo è costituito principalmente da finestre alte, ben fatte e senza tende, una o più delle quali fungono da porte. Non c'è molto da dire o da vedere dell'esterno. Veniamo a sapere che la casa sorge nel tipico parco inglese dell'epoca. Forse ne vediamo una indicazione, forse solo luce, aria e cielo.

La stanza appare spoglia nonostante il grande tavolo che ne occupa il centro. Il tavolo, le sedie dallo schienale dritto e, l'unico altro elemento di arredo, il tavolo da disegno, sarebbero ora tutti pezzi da collezione, ma qui, su un pavimento di legno senza moquette, non hanno più pretese di un'aula scolastica, che è in effetti l'uso principale di questa stanza in questo momento. L'eleganza che c'è, è architettonica, e niente è impressionante se non la scala. C'è una porta in ciascuna delle pareti laterali. Queste sono chiuse, ma una delle portefinestre è aperta su un mattino luminoso ma senza sole.

Ci sono due persone, ognuna occupata con libri, carta, penna e inchiostro, occupate separatamente. L'allieva è THOMASINA COVERLY, 13 anni. Il tutor è SEPTIMUS HODGE, 22 anni. Ciascuno ha un libro aperto.

(...)

THOMASINA: Septimus, cos'è l'abbraccio carnale?

SEPTIMUS: L'abbraccio carnale è la pratica di gettare le braccia attorno a un pezzo di carne.

THOMASINA: Tutto qui?

SEPTIMUS: No… una spalla di montone, una coscia di cervo ben abbracciata, un abbraccio di gallo cedrone... caro, carnis-, femminile; carne.

THOMASINA: È peccato?

SEPTIMUS: Non necessariamente, mia signora, ma quando l'abbraccio carnale è peccaminoso è un peccato della carne, QED. (...) Pensavo stessi trovando una dimostrazione per l'ultimo teorema di Fermat.

THOMASINA: È molto difficile, Septimus. Dovrai mostrarmi come.

SEPTIMUS: Se sapessi come fare, non ci sarebbe bisogno di chiederlo. L'ultimo teorema di Fermat ha tenuto occupate le persone per centocinquanta anni, e speravo che ti avrebbe tenuto occupata abbastanza a lungo da permettermi di leggere la poesia di Mr. Chater in lode dell'amore con la sola distrazione delle sue stesse assurdità.

THOMASINA: Il nostro signor Chater ha scritto una poesia?

SEPTIMUS: Crede di aver scritto una poesia, sì. Vedo che potrebbe esserci più carnalità nella tua algebra che nel "Divano dell'eros" di Mr. Chater. THOMASINA: Oh, non era la mia algebra. Ho sentito [il maggiordomo] Jellaby dire alla cuoca che la signora Chater è stata scoperta in un abbraccio carnale nel gazebo.

(...)

THOMASINA: L'abbraccio carnale è un bacio?

SEPTIMUS: Sì.

THOMASINA: E abbracciare la signora Chater?

SEPTIMUS: Sì. Ora, l'ultimo teorema di Fermat.

THOMASINA: Lo pensavo. Spero che te ne vergogni.

SEPTIMUS: Io, mia signora?

THOMASINA: Se non mi insegni tu il vero significato delle cose, chi lo farà?

SEPTIMUS: Ah. Sì, mi vergogno. L'abbraccio carnale è il congresso sessuale, che è l'inserimento dell'organo genitale maschile nell’organo genitale femminile per scopi di procreazione e piacere. L'ultimo teorema di Fermat, invece, afferma che, quando x, y e z sono numeri interi elevati ciascuno alla potenza di n, la somma dei primi due non può mai essere uguale al terzo quando n è maggiore di 2.

(Pausa.)

THOMASINA: Puah!

SEPTIMUS: Tuttavia, questo è il teorema.

THOMASINA: È disgustoso e incomprensibile. Ora, quando sarò cresciuta per risolverlo da sola, non lo farò mai senza pensare a te.

Thomasina è una giovane ragazza di tredici anni che studia algebra e geometria. Ma non è la tipica studentessa di matematica; come diventa chiaro man mano che la commedia si svolge, Thomasina è un genio che non solo mette in discussione le fondamenta stesse della matematica, ma si prepara anche a cambiare la direzione di innumerevoli secoli di pensiero matematico.

A Thomasina non piace la geometria euclidea. All'inizio della commedia rimprovera Septimus, "Ogni settimana traccio le tue equazioni punto per punto, x contro y in ogni sorta di relazione algebrica, e ogni settimana si disegnano come geometria ordinaria, come se il mondo delle forme non fosse niente che archi e angoli. Verità di Dio, Septimus, se c'è un'equazione per una campana, allora ci deve essere un'equazione per una campanula, e se una campanula, perché non una rosa?" Così decide di abbandonare la geometria euclidea classica per scoprire l'equazione di una foglia, ma potrebbe aver cercato, se l’avesse conosciuto, quella di un broccolo romanesco.

Galileo pensava che “il libro della natura è scritto in lingua matematica, e i caratteri sono triangoli, cerchi ed altre figure geometriche”. Ora, nella nostra esperienza quotidiana, il cerchio, il triangolo equilatero e le figure geometriche in generale sono un'eccezione e non la regola, anzi si può dire che esse non esistano in natura, ma solo come astrazione. Siamo portati dunque a chiederci quale sia la forma di un albero, di una montagna o di una nuvola. Per Galileo anche tali enti ricadevano sotto il campo della geometria, ma la matematica ha sempre preferito studiare la realtà ricercando di ogni fenomeno le sue caratteristiche più semplici, che potessero essere trattate evidenziandone la regolarità e l’armonia, ritenendo che non si potessero studiare oggetti reali dotati di un alto grado di complessità quali la forma di una montagna, o di un albero.

In questa ricerca di un modello sempre più aderente alla realtà, l’introduzione dei frattali ha consentito di compiere passi da gigante, in quanto tramite essi è possibile descrivere oggetti naturali (alberi, coste, il sistema sanguigno...) e fenomeni fisici che sembrano dominati dal caso (la disposizione delle galassie, la sequenza delle piene di un fiume, la frequenza degli errori nelle trasmissioni telefoniche, …), aspetti soltanto sfiorati dalla matematica e dalla geometria classica.

Lady Croom, la madre di Thomasina, capisce poco del potenziale intellettuale della figlia. Thomasina è mutevole, intensa, brillante e affascinante. Ha un rispetto senza compromessi per i fatti e la verità che si trova nei matematici e nei bambini.

L '"abbraccio carnale" a cui si riferisce Thomasina è solo uno dei tanti che si svolgono a Sidley Park, la tenuta dei Coverly. In effetti, il groviglio di amori incrociati di Arcadia ricorda le commedie vaudeville, anche perché Stoppard non fa mancare brillanti equivoci e doppi sensi.

Septimus (compagno di studi e amico di Byron) ha davvero avuto un'avventura con la moglie di Ezra Chater, un poetastro e botanico che è in visita a Sidley Park. Il vero amore di Septimus è però Lady Croom. Abbastanza non tradizionale, tuttavia, è la mutevole virtù di Lady Croom: si diverte con un pianista polacco in visita, con il suo vicino Lord Byron (che mai compare in scena) e, verso la fine della commedia, con lo stesso Septimus.

Quando lo spettacolo avanza fino ai giorni nostri, Sidley Park è la casa dell'ultima generazione dei Coverly. L'azione odierna si svolge sulla stessa scena, e i costumi sono l'unica indicazione che il tempo è diverso. L’erede dei Coverly, Valentine, è un matematico a Oxford. Usando duecento anni di cronache sui passatempi di Sidley Park (elenchi delle prede uccise durante le battute di caccia), egli sta esaminando i cambiamenti nella popolazione dei galli cedroni. A causa della caccia, dei cambiamenti del regime alimentare e di altri fattori, la popolazione di galli cedroni non è facilmente descritta da una funzione logistica; quindi, Valentine sta cercando di formulare un modello più complesso. A poco a poco, Valentine viene a conoscenza di alcuni dei vecchi misteri che circondano Sidley Park, comprese le scoperte di Thomasina, e questo pone le basi per una serie unica di scene che saltano avanti e indietro tra l'inizio del XIX secolo e il presente.

La matematica non è l'unico tema di questa commedia, ovviamente, ma le idee di geometria regolare contro irregolare o caos contro ordine sembrano pervadere tutti gli altri eventi che si verificano a Sidley Park. Siamo spinti ad esempio in un dibattito sugli stili paesaggistici britannici che caratterizzano lo stile classico ordinato contro lo stile irregolare, "pittoresco" che stava diventando di moda agli inizi dell’Ottocento e di cui era propugnatore il paesaggista Richard Noakes, nella residenza con l’incarico di rivoluzionare il giardino (tra i primi utilizzatori della macchina di Newcomen per drenare un lago).

La fiancée (forse) di Valentine, Hannah Jarvis, autrice di libri di successo sui giardini storici, procede metodicamente a scoprire i segreti di Sidley Park, in netto contrasto con la sua antitesi, l’affascinante e arrogante Bernard Nightingale, uno studioso di lettere della Sussex University che fa irruzione nella biblioteca di Sidley Park in cerca di prove che Byron aveva visitato la residenza, ma salta da una teoria all'altra con spericolata leggerezza. In effetti, l'intera commedia contrappone il razionalismo di Newton al romanticismo di Byron.

La teoria di Nightingale (Chater sarebbe stato ucciso in duello da Byron nella tenuta a causa di una perfida recensione), che annuncia in una conferenza stampa, viene diffusa su tutti i giornali ma viene rapidamente minata dalla scoperta di Hannah che Chater è morto in Martinica per il morso di una scimmia (dopo aver scoperto e descritto una nuova specie di dalia). All'estremo opposto, Valentine, essendo un matematico, è molto più circospetto e preciso nelle sue ricerche. Ma è Hannah che si rivela avere la vera anima di un'esploratrice. Ad un certo punto, Valentine vuole abbandonare il progetto sui galli cedroni, ma Hannah gli dice di non arrendersi. "È voler sapere che ci rende importanti", dice. "Altrimenti usciremo da dove siamo entrati."

In una delle scene più brillanti della commedia, Bernard offre a Valentine un'appassionata tirata contro la scienza. "Oh, mi fulminerai con penicillina e pesticidi. Risparmiami quello e ti risparmierò la bomba e gli aerosol. Ma non confondere il progresso con la perfettibilità. Un grande poeta è sempre puntuale. Un grande filosofo è un bisogno urgente. Non c'è fretta per Isaac Newton. Eravamo abbastanza contenti del cosmo di Aristotele. Personalmente l'ho preferito. Cinquantacinque sfere di cristallo agganciate all'albero motore di Dio sono la mia idea di un universo soddisfacente. Non riesco a pensare a niente di più banale della velocità della luce. Quark, quasar - big bang, buchi neri - a chi [importa]? Come ci avete fregato con tutta quella roba? Tutti quei soldi? E perché siete così soddisfatti di voi stessi?". E poi, alla fine della sua tirata, cita dolcemente Byron:

“She walks in beauty, like the night

Of cloudless climes and starry skies;

And all that’s best of dark and bright

Meet in her aspect and her eyes”

(“Cammina nella bellezza, come la notte / di climi senza nuvole e cieli stellati, e tutto ciò che c'è di meglio dell’oscurità e della luce / incontra nel suo aspetto e nei suoi occhi”).

Il passaggio dal comico al serio funziona: nonostante le visioni retrive della scienza, Bernard ha illuminato un regno in cui la scienza non può avventurarsi. Ciò conduce a una delle domande centrali dell'opera: fino a che punto la scienza e la matematica possono portarci nello spiegare cos'è la vita? Il destino di Septimus è che doveva essere reso pazzo da ciò che Thomasina aveva previsto: la seconda legge della termodinamica assicura che il mondo diventerà sempre più incoerente e disorganizzato.

All’inizio dell’opera, Thomasina così si rivolge a Septimus:

THOMASINA: Quando mescoli il tuo budino di riso, Septimus, il cucchiaio di marmellata si spande intorno formando scie rosse come l'immagine di una meteora nel mio atlante astronomico. Ma se mescoli all'indietro, la marmellata non si unirà più. Il budino, infatti, non se ne accorge e continua a tingersi di rosa proprio come prima. Non pensi che sia strano?"

SEPTIMUS: No.

THOMASINA: Beh, lo so. Non puoi separare le cose.

SEPTIMUS: Non puoi più, il tempo dovrebbe necessariamente scorrere all'indietro, e poiché non lo farà, dobbiamo muoverci in avanti mescolando mentre procediamo, il disordine fuori dall'ordine nel disordine finché il rosa non è completo, immutato e immutabile, e abbiamo chiuso per sempre. Questo è noto come libero arbitrio o autodeterminazione.

Questa scena rivela la curiosità scientifica di Thomasina: anche mentre mescola il budino di riso, tenta di trovare spiegazioni scientifiche per il mondo che la circonda. Le scie di marmellata si muovono verso un disordine più ampio che non può essere rimescolato andando nella direzione opposta. Questo entropico movimento verso un disordine sempre maggiore è caratteristico della teoria del caos, come spiegato più avanti da Valentine. La teoría del caos, spiega Valentine ad Hannah, aiuta gli scienziati ad avvicinarsi agli avvenimenti quotidiani delle cose che li circondano da "ciò che accade in una tazza di caffè".

La sua comprensione che l'algebra era inadeguata a descrivere la natura tormenta Septimus fino alla fine dei suoi giorni. Hannah legge da una vecchia lettera che descrive la vita di Septimus, che finisce i suoi giorni come eremita per trent’anni in una capanna nel giardino della tenuta: era la “matematica francesizzata” che lo ha portato alla malinconica certezza di un mondo senza luce o vita ... come una stufa a legna che deve consumarsi finché cenere e stufa non sono come uno, e il calore è scomparso dalla terra. Hannah legge che” morì a 47 anni, canuto come Giobbe e magro come un torsolo di cavolo”, perseguitato dall’idea della morte termica dell’universo preconizzata da Thomasina. Arcadia presenta un'immagine affascinante di ciò che può accadere quando le persone si preoccupano davvero di ciò che la scienza e la matematica hanno da dire.

Hannah scopre alcuni vecchi taccuini in cui sembra che Thomasina abbia iniziato a sperimentare iterazioni di funzioni. Sebbene lo stesso Valentine stia usando l'iterazione per modellare la popolazione di galli cedroni, resiste all'idea che ciò che ha fatto Thomasina assomigli al suo stesso lavoro, protestando che avrebbe studiato solo matematica classica e che i suoi sarebbero stati solo divertimenti numerici. Dopo il suo tempo, "la matematica si è lasciata alle spalle il mondo reale, proprio come l'arte moderna, davvero", dice. “La natura era classica, la matematica era improvvisamente Picasso. Ma ora la natura sta avendo l'ultima risata. Le cose bizzarre si stanno rivelando essere la matematica del mondo naturale”.

Thomasina ha scoperto la procedura matematica che ora è chiamata sistema di funzioni iterate. Hannah chiede a Valentine come fa. Val spiega che un algoritmo è una ricetta, che se conoscessimo la ricetta per produrre una foglia, potremmo facilmente iterare l'algoritmo per disegnare un'immagine della foglia. "La matematica non è difficile. È quello che hai fatto a scuola. Hai un'equazione in x e y. Qualsiasi valore per x ti dà un valore per y. Quindi metti un punto dove è giusto sia per x che per y. Poi prendi il prossimo valore per x che ti dà un altro valore per y... quello che sta facendo è, ogni volta che calcola un valore per y, lo usi come prossimo valore per x. E così via: feedback.... Se conoscessi l'algoritmo e lo inviassi in risposta, diciamo diecimila volte, ogni volta ci sarebbe un punto da qualche parte sul piano. Non sapresti mai dove aspettarti il punto successivo. Ma gradualmente inizi a vedere questa forma, perché ogni punto sarà all'interno della forma di questa foglia."

Un sistema di funzioni iterate è un insieme di n trasformazioni affini (rotazioni, omotetie, traslazioni, rototraslazioni, riflessioni che non sono necessariamente isometrie, non preservano, cioè, angoli e distanze, mentre mantengono sempre il parallelismo tra le rette) che agisce sulla scala degli oggetti trattati.

Normalmente, vengono utilizzati due tipi di algoritmi, la versione deterministica o quella casuale.

L'algoritmo deterministico consiste nel prendere un insieme di punti, che può essere una qualsiasi figura geometrica, e applicarvi ciascuna delle n trasformazioni affini del sistema, per cui otteniamo n serie di punti trasformati. A ognuno di essi applichiamo di nuovo ognuna delle n funzioni, ottenendo n2 nuove serie di punti. Continuiamo in questo modo iterando i risultati, fino a quando l'unione di tutti gli insiemi ottenuti nell'ultima iterazione si avvicina sufficientemente alla figura che costituisce l'attrattore del sistema. Arriveremo sempre a questo attrattore, indipendentemente dall’insieme iniziale di punti selezionato. Normalmente, non ci vogliono molte iterazioni per ottenere questo insieme frattale.

Uno degli attrattori più comuni è il Triangolo di Sierpinski, un frattale così chiamato dal nome di Wacław Sierpiński, che lo descrisse nel 1915. È un esempio base di insieme auto-similare, cioè matematicamente generato da un pattern che si ripete allo stesso modo su scale diverse. Nell’immagine si può vedere come si ottiene da un triangolo equilatero, ma si potrebbe ottenere da qualsiasi altra figura.

Ancora più antica è la Curva di Koch, che fu descritta per la prima nel 1904 dal matematico svedese Helge von Koch. La generazione della curva di Koch avviene grazie all'esecuzione ripetuta di un programma di istruzioni o procedura ricorsiva: è una procedura perché precisamente definita da un numero finito di passi, è ricorsiva perché viene ripetuta meccanicamente. L'algoritmo della curva consiste nella ripetizione del ciclo sottostante:

Partendo da un segmento di determinata lunghezza:

• dividere il segmento in tre segmenti uguali;

• cancellare il segmento centrale, sostituendolo con due segmenti identici che costituiscono i due lati di un triangolo equilatero;

• tornare al punto 1 per ognuno dei nuovi segmenti.

Partendo da un segmento, se ne ottengono quindi quattro (costituenti una linea spezzata) nel primo ciclo, 4x4=16 nel secondo ciclo e così via, generando al limite un elegantissimo frattale. Ingrandendo un qualunque dettaglio del frattale si ottiene ancora lo stesso frattale: in questo consiste l'autosimilarità e la struttura fine dei frattali a qualunque livello di scala.

Il fiocco di neve di Von Koch è una curva costruita operando nello stesso modo sui lati di un triangolo equilatero: si prende il lato, lo si taglia in 3 parti e si sostituisce quella centrale con due segmenti uguali a quello eliminato; si ripete l’operazione con ciascuno dei quattro segmenti così ottenuti e si continua per un numero infinito di volte. La figura che si ottiene, operando sui tre lati, dopo un numero infinito di iterazioni è il fiocco di neve di Koch. Mentre il merletto di Von Koch è chiaramente autosimilare, il fiocco di neve non lo è. Infatti, ingrandendo uno dei lati dopo la prima iterazione otteniamo una copia del merletto e non del fiocco.

L'algoritmo casuale è simile, ma invece di applicare le funzioni a un insieme di punti, li applichiamo di seguito a un singolo punto, disegnando il risultato ogni volta. Assegniamo un valore di probabilità a ciascuna delle trasformazioni del sistema, tenendo conto che la somma totale dei valori di probabilità delle funzioni deve essere 1. In ogni iterazione dell'algoritmo, selezioniamo una delle trasformazioni con probabilità p. Per far questo è sufficiente ottenere un valore casuale compreso tra 0 e 1 e aggiungere le probabilità di ciascuna funzione una alla volta fino a ottenere un risultato maggiore del numero casuale ottenuto. Questa sarà la funzione selezionata. I primi punti della serie vengono scartati. Poiché di solito sono molto lontani dall'attrattore, il resto viene tracciato fino a ottenere il disegno frattale corrispondente, il che avviene solitamente dopo un numero di iterazioni compreso tra 1000 e 5000.

Assegnando dei valori di probabilità alle nostre trasformazioni possiamo “guidare” l’algoritmo verso forme autosimili che imitano oggetti naturali. Uno dei frattali biomorfi più riusciti è la foglia di felce, i cui dettagli riproducono sempre la stessa immagine di partenza. L’immagine in questione, chiamata felce di Barnsley dal nome del matematico che rese popolare questa procedura, pur essendo creata a computer, è molto simile ad una felce reale.

Valentine si diverte chiaramente in questa nuova matematica. "L'imprevedibile e il predeterminato si svolgono insieme per rendere tutto così com'è", dichiara. "È così che la natura si crea, su ogni scala, il fiocco di neve e la tempesta di neve."

Mentre Thomasina lotta con la sua nuova geometria, c'è uno sviluppo matematico parallelo in atto nell'opera. Valentine sta cercando di utilizzare l’iterazione di funzioni per spiegare l’andamento della popolazione di galli cedroni nella tenuta di Sidley Park. Conosce i dati sulle uccisioni di galli cedroni nella tenuta negli ultimi duecento anni e vorrebbe estrapolarli per prevedere le popolazioni future. Curiosamente, sta usando esattamente la stessa tecnica che Thomasina aveva sperimentato anni prima. Beh, non proprio. Come spiega Valentine, "In realtà lo sto facendo dall'altra parte. Lei ha iniziato con un'equazione e l'ha trasformata in un grafico. Ho un grafico - dati reali - e sto cercando di trovare l'equazione che darebbe il grafico se lo usassi nel modo in cui lei usava il suo. L'ho iterato. (...) È il modo in cui guardi ai cambiamenti della popolazione in biologia. Pesci rossi in uno stagno, diciamo. Quest'anno ci sono x pesci rossi. L'anno prossimo ci saranno y pesci rossi. Alcuni nascono, altri vengono mangiati dagli aironi, qualunque cosa. La natura manipola la x e la trasforma in y. Quindi y pesci rossi sono la tua popolazione iniziale per l'anno successivo. Proprio come Thomasina. Il tuo valore per y diventa il tuo prossimo valore per x. La domanda è: cosa succede a x? Qual è la manipolazione? Qualunque cosa sia, può essere scritta in matematica. Si chiama algoritmo”.

Uno degli algoritmi di questo tipo più semplici utilizzati dai biologi delle popolazioni è l'equazione logistica, nota anche come modello di Verhulst, un modello di crescita della popolazione che descrive una crescita con “andamento ad S”: lenta crescita iniziale, seguita da un’accelerazione e poi da un successivo rallentamento in prossimità̀ del valore massimo permesso, che costituisce un limite asintotico della funzione dove non c’è più̀ crescita. Secondo questo modello, il tasso di riproduzione è proporzionale alla popolazione esistente e all’ammontare delle risorse disponibili. Esistono anche strumenti matematici più raffinati, come ad esempio l’equazione di Lotka-Volterra, ma non è qui il caso di complicare le cose.

Stoppard ha capito qualcosa del cuore poetico di quest'area della matematica. Descrivendo i suoi sforzi con i dati "pieni di rumore" che ha sulla popolazione dei galli cedroni, Valentine dice che è "come un pianoforte nella stanza accanto: sta suonando la tua canzone, ma sfortunatamente è fuori controllo, mancano alcune corde e il pianista è stonato e ubriaco ... [quindi] inizi a indovinare quale potrebbe essere la melodia. Cerchi di distinguerlo dal rumore. Provi questo, provi quello, inizi a ottenere qualcosa: è cotto a metà, ma inizi a inserire note che mancano o non sono proprio le note giuste. E poco alla volta...” E comincia a canticchiare “Happy Birthday to You”.

L'andamento di una popolazione in natura viene condizionato da diversi fattori che costituiscono la cosiddetta resistenza ambientale e che pongono un limite a tale sviluppo. Per cui una data popolazione avrà sì un accrescimento esponenziale, ma solo inizialmente, per poi subire un flesso ad un certo punto a causa della resistenza ambientale, la quale pone un limite superiore alla curva sotto forma di un asintoto orizzontale K, per cui tale curva avrà̀ un andamento sigmoidale. L'asintoto rappresenta l'equilibrio raggiunto tra popolazione ed ecosistema. Tale parametro è di tipo sperimentale e dipende dalle condizioni iniziali. Come tale, dovrebbe rimanere costante. In realtà̀ l'ambiente è un sistema dinamico, soggetto quindi a continue variazioni, e, di conseguenza, sia l'asintoto sia la curva di accrescimento di una certa popolazione subiscono continue fluttuazioni in ragione di di diversi fattori limitanti (disponibilità di cibo, epidemie, predatori, tra cui l’uomo, ecc.). In ragione delle condizioni iniziali e dell’evoluzione del sistema, l’andamento della popolazione può convergere verso attrattori molto diversi, da un comportamento più o meno stabile a uno più o meno ciclico, che varia nel tempo entro certi limiti, a uno caotico (deterministico), assolutamente imprevedibile, e il pianista sembra pigiare sui tasti in modo casuale: la melodia ci è inaccessibile, o, diremmo, indecidibile.

L'opera di Stoppard approfondisce l'inquietante esperienza di nuove idee, l'interazione tra ipotesi e prove e il ruolo del carattere umano nella scoperta. Si tratta di argomenti difficili, eppure la conversazione rimane vivace e divertente e i personaggi coinvolgenti e confusi in modi molto umani.

Arcadia funge da utile antidoto all'impressione che molte persone hanno che la matematica non sia cambiata molto dai tempi di Euclide e generalmente proceda con incrementi imperscrutabili. La matematica si evolve e ha il potere di riorganizzare il modo in cui pensiamo al mondo che ci circonda.

Lo commedia porta anche la matematica a "... le cose di dimensioni ordinarie che sono le nostre vite, le cose su cui le persone scrivono poesie - nuvole - narcisi - cascate - e cosa succede in una tazza di caffè quando entra la panna".

Alla fine dello spettacolo, i personaggi degli anni '90 si vestono in abiti antiquati in preparazione di un ballo che si terrà a Sidley Park. E poi a un certo punto, mentre Hannah e Valentine si siedono a leggere, Thomasina e suo fratello entrano improvvisamente nella stanza, due bambini che si prendono in giro a vicenda. Personaggi di entrambe le epoche, che erano stati separati nelle scene precedenti, appaiono improvvisamente sul palco insieme. L'effetto è magico, rafforzando la sensazione che, sebbene il mondo sia imprevedibile, gli schemi emergono e riappaiono con il passare del tempo. Un attimo dopo, Valentine e Septimus stanno, nei loro tempi separati, esaminando il rozzo disegno di Thomasina di un motore termico, prova concreta che aveva anticipato la seconda legge della termodinamica (mentre da Parigi giunge la notizia che il rendimento di una macchina termica non può mai essere del 100%). Come una palla che rompe una lastra di vetro, dice Valentine, "Puoi rimettere a posto i pezzi di vetro, ma non puoi raccogliere il calore dello scontro". "Quindi l'Universo newtoniano migliorato deve cessare e raffreddarsi", fa eco Septimus.

La musica arriva da dietro le quinte e Thomasina implora Septimus di insegnarle a ballare il valzer. Ma è perso nei suoi pensieri e le dice: "Quando avremo trovato tutti i misteri e perso tutto il significato, saremo soli, su una spiaggia deserta". La soluzione che propone risuona come una campana suonata nel cuore della notte: "Allora balleremo!" A differenza di Septimus, Thomasina può scandagliare le profondità della matematica e riemergere con la sua esuberanza intatta per la vita. Stoppard, intanto, ci ha informato che sarebbe morta nell’incendio della sua camera appena compiuti i diciotto anni e che, sì, un bacio a Septimus l’aveva dato, nell’eremo appena costruito e ancora vuoto.