C’è qualcosa che mi attira verso gli uomini di scienza dell’età vittoriana. Intellettuali completi, a loro agio con i numeri e con le lettere, specialisti in più discipline, riuniti in associazioni prestigiose di tradizione secolare, eppure pronti a intonare cori conviviali alla sera davanti a una birra. Nei decenni centrali dell’Ottocento, il Regno Unito visse una fase di grande fermento scientifico, un’epoca in cui, alle conquiste territoriali ed economiche accompagnate dalle note di Rule Britannia!, si associò una rilevante posizione in pressoché tutti i campi della ricerca.
La poesia era considerata una delle più alte espressioni artistiche e godeva di una vasta popolarità, almeno nei ceti che avevano accesso all’istruzione. Molti matematici e fisici erano poeti dilettanti, ma il loro diletto si fondava su solide basi culturali (e persino su una vera e propria erudizione) e si manifestò con opere di buon livello. Era infatti tra loro condiviso il pensiero che la ricerca matematica richiede un alto grado di immaginazione, affine all’istinto creativo del poeta.
Il più noto dei matematici-poeti dell’epoca fu senza dubbio James Clerk Maxwell (1831-1879), uno dei più grandi fisici dell’Ottocento, al quale tempo fa ho dedicato una serie di articoli (1, 2 e 3). La più celebre poesia di Maxwell, scritta nell’inglese degli scozzesi, è senza dubbio questa parodia di un’opera del bardo scozzese Robert Burns, che il fisico dedicò ai problemi con il gentil sesso di un collega e che cantava accompagnandosi con la chitarra:
Gin a body meet a body
Flyin' thro the air,
Gin a body hit a body,
Will it fly? And where?
Ilka impact has its measure
Ne'er a' ane hae I
Yet a' the lads they measure me,
Or, at least, they try.
Gin a body meet a body
Altogether free,
How they travel afterwards
We do not always see.
Ilka problem has its method
By analytics high;
For me, I ken na ane o' them,
But what the waur am I?
Se un corpo incontra un corpo
volando in mezzo all’aria,
se un corpo urta un corpo
Volerà? E dove?
Ogni impatto ha la sua misura,
io non ne ho mai avuto uno,
eppure le donne loro mi misurano,
o, almeno, ci provano.
Se un corpo incontra un corpo,
tutti insieme in libertà,
come viaggiano in seguito
non sempre lo si vedrà.
Ogni problema ha il suo metodo
secondo le analitiche altezze;
io, io non ne conosco alcuno,
ma come sono sfortunato!
Augustus De Morgan (1806-1871), uno dei fondatori della logica matematica, possedeva un’erudizione enciclopedica, ben al di là del suo campo d’attività professionale: basti dire che fu il compilatore di alcune delle voci della più diffusa enciclopedia mitologica dei suoi tempi. De Morgan si cimentò anch’egli con la parodia, scrivendo ad esempio questa quartina sulle pulci da Jonathan Swift, che, se vogliamo, è un’anticipazione delle geometria frattale:
Great fleas have little fleas upon their backs to bite 'em,
And little fleas have lesser fleas, and so ad infinitum.
And the great fleas themselves, in turn, have greater fleas to go on;
While these again have greater still, and greater still, and so on.
Le grandi pulci portano piccole pulci che le mordono con appetito,
e le pulci piccole hanno pulci più piccole, e così all’infinito.
E le stesse grandi pulci, a loro volta, hanno pulci più grandi per campare;
mentre queste ne hanno di ancor più grandi, e più grandi, e via andare.
Il matematico londinese scrisse anche il gustoso A Budget of Paradoxes, pubblicato postumo dalla moglie nel 1872, una raccolta divertente di considerazioni, aneddoti, recensioni, citazioni sulla matematica, la scienza, la religione, compresa un’analisi dei rapporti tra scrittori ed editori, una pagina con centinaia di anagrammi del suo cognome (come Great gun! Do us a sum!), una serie di vivaci descrizioni del mondo scientifico inglese a lui contemporaneo. De Morgan si dimostra scrittore di talento, esponendo le sue conoscenze con la vivacità di un moderno divulgatore e, nel solco della buona tradizione anglosassone, con uno humour che non esita a far ricorso all’aneddoto curioso, al gioco di parole, alla poesia umoristica o nonsensical.
La passione poetica non risparmiò neppure William Rowan Hamilton (1805-1865), il padre dei quaternioni, il quale, bambino prodigio, secondo i biografi conosceva una decine di lingue tra moderne e antiche (ebraico, arabo e persiano compresi) e a cinque anni, sotto la guida dello zio prete, recitava le opere di Dryden, Collins, Milton e Omero. All’età di ventidue anni, poco prima di diventare assistente dell’osservatorio astronomico di Dunsink, presso Dublino, Hamilton intraprese un viaggio attraverso l’Inghilterra e la Scozia, durante il quale fu ospite per una notte del poeta William Wordsworth nella casa di costui nel Cumberland. Il poeta ricambiò la visita quando Hamilton aveva preso posto all’osservatorio e, a partire da quell’occasione, ricevette dall’uomo di scienza diverse sue poesie. Poco tempo dopo inviò una lettera, che si è conservata, nella quale, con tatto ma senza tante perifrasi, invitava Hamilton a dedicarsi alla scienza o, piuttosto, alla prosa: l’immaginazione poetica non gli mancava, ma la tecnica era carente e non si poteva improvvisare. Questo è l’incipit della fine dei sogni poetici di Hamilton:
"You send me showers of verses which I receive with much pleasure, as do we all: yet have we fears that this employment may seduce you from the path of science which you seem destined to tread with so much honor to yourself and profit to others”. Again and again I must repeat that the composition of verse is infinitely more of an art than men are prepared to believe, and absolute success in it depends upon innumerable minutiae which it grieves me you should stoop to acquire a knowledge of.”
“Mi avete inviato valanghe di versi, che ho ricevuto con molto piacere, come è usanza fare: tuttavia temiamo che questo impegno possa allontanarvi dal cammino della scienza che sembrate destinato a percorrere con molto onore per voi stesso e profitto per gli altri. Ancora una volta sono costretto a ripetere che la composizione di un verso è infinitamente più un’arte di quanto gli uomini siano preparati a credere, e il successo assoluto in essa dipende da innumerevoli minuzie delle quali mi addolora [dirvi] voi dovreste chinarvi [sui libri] per acquisire una conoscenza”.
Matematico, poliglotta, poeta e traduttore fu James Joseph Sylvester (1814-1897), che diede contributi fondamentali alla teoria delle matrici, a quella degli invarianti, alla teoria dei numeri, a quella della divisibilità e al calcolo combinatorio. Molti dei suoi lavori matematici contengono citazioni prese dalla poesia classica. Nel 1870 pubblicò un libro intitolato The Laws of Verse, che contiene molte sue traduzioni di poeti greci e latini, nel quale tentò di codificare le regole di metrica inglese per la poesia.
Quando divenne professore saviliano di Geometria a Oxford, Sylvester tenne nel 1885 la sua lettura inaugurale, che verteva sugli invarianti differenziali, che egli definiva reciprocanti. Un reciprocante elementare è 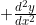 , perché se
, perché se 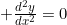 , allora
, allora 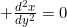 . Egli considerava questa come la forma “larva”, e da essa sviluppò la “crisalide”
. Egli considerava questa come la forma “larva”, e da essa sviluppò la “crisalide”
E la “imago”
Si vede che l’espressione “crisalide” è asimmetrica: il posto del nono termine è vacante. Ciò mosse l’immaginazione poetica di Sylvester, che introdusse nella sua prolusione il seguente sonetto:
To a Missing Member of a Family Group of Terms in an Algebraical Formula
Lone and discarded one ! divorced by fate,
Far from thy wished-for fellows—whither art flown?
Where lingerest thou in thy bereaved estate,
Like some lost star, or buried meteor stone?
Thou minds't me much of that presumptuous one,
Who loth, aught less than greatest, to be great.
From Heaven's immensity fell headlong down
To live forlorn, self-centred, desolate:
Or who, new Heraklid, hard exile bore,
Now buoyed by hope, now stretched on rack of fear,
Till throned Astraea, wafting to his ear
Words of dim portent through the Atlantic roar,
Bade him " the sanctuary of the Muse revere
And strew with flame the dust of Isis' shore."
Al membro mancante di un gruppo famigliare di termini in una formula algebrica
Solitario, messo da parte, separato dal destino,
lontano dai compagni bramati - dove sei volato?
Dove indugiasti nella tua orbata condizione,
come una stella perduta, o un meteorite sepolto?
Tu mi porti alla mente assai quel presuntuoso,
che superbo, quasi il più grande, per essere grande,
dall’immensità del Cielo precipitò a testa in giù
per vivere misero, in sé racchiuso, desolato,
o colui che, novello Eraclide, patì un duro esilio,
ora animato dalla speranza, ora torturato dalla paura,
finché la regale Astrea, gli sussurrò all'orecchio
parole di vago portento nel mugghio dell’Atlantico,
gli comandò “il santuario della Musa riverisci
e cospargi di fiamme la polvere della costa di Iside”.
Dove il riferimento della seconda quartina è a Lucifero e alla sua caduta, mentre quello della prima terzina sembra a un discendente di Ercole (un Eraclide), forse Ippote, che fu esiliato per dieci anni dopo aver ucciso l’indovino che aveva predetto la distruzione dell'esercito degli Eraclidi se fossero tornati nel Peloponneso. La mia scarsa cultura classica non giunge a ritrovare il racconto mitologico d’origine (confido in qualche lettore maggiormente ferrato di me nella materia).
L’ultimo poeta di questa rassegna è il matematico e filosofo William Kingdon Clifford (1845-1879), morto giovane di tubercolosi, oggi ricordato soprattutto per la sua eponima algebra di Clifford, un'algebra associativa che generalizza i numeri complessi e i quaternioni di Hamilton. La sua teoria lo condusse, in seguito, agli ottonioni (o biquaternioni), oggetti matematici che impiegò per studiare il movimento negli spazi non-euclidei e sulle superfici ora conosciute come spazi di Klein-Clifford. La sua teoria dei grafi fu anticipatoria di molte acquisizioni successive. Inoltre sviluppò profondo interesse anche per la topologia, l'algebra universale e le funzioni ellittiche.
Uomo di singolare acutezza e originalità, Clifford era dotato di uno stile lucido, di profondità e immaginazione poetica e di un grande calore umano. Razionalista e osteggiato dalle gerarchie ecclesiastiche, sosteneva che fosse immorale credere alle cose per cui non vi è una prova: nel suo saggio The Ethics of Belief (1879) compare il famoso principio: "è sbagliato sempre, comunque e per chiunque, credere a qualsiasi cosa basandosi su prove insufficienti." Scrisse una fiaba per bambini, The Little People, e diverse poesie, con stile leggero e personale. Ecco ad esempio i bellissimi versi che inviò a George Eliot come accompagnamento a una copia della sua fiaba:
Baby drew a little house,
Drew it all askew;
Mother saw the crooked door
And the window too.
Mother heart, whose wide embrace
Holds the hearts of men,
Grows with all our growing hopes,
Gives them birth again,
Listen to this baby-talk:
'Tisn't wise or clear;
But what baby-sense it has
Is for you to hear.
Il piccolo disegnò una casetta,
la disegnò tutta storta;
la mamma vide la porta sbilenca
e pure la finestra.
Madre natura, il cui largo abbraccio
cinge i cuori degli uomini,
cresce con tutte le nostre crescenti speranze,
dà loro nascita di nuovo.
Ascoltate questo discorso di bimbo:
non è saggio né chiaro;
ma per il senso bambino che possiede
lo dovete ascoltare.
In un discorso dal titolo Alcune delle condizioni dello sviluppo mentale, che pronunciò alla Royal Institution nel 1868, quando aveva 23 anni, egli affrontò il tema del rapporto tra scienza e arte con queste parole, che mi sembra possano essere descrittive del clima culturale di un’epoca:
"Men of science have to deal with extremely abstract and general conceptions. By constant use and familiarity, these, and the relations between them, become just as real and external as the ordinary objects of experience, and the perception of new relations among them is so rapid, the correspondence of the mind to external circumstances so great, that a real scientific sense is developed, by which things are perceived as immediately and truly as I see you now. Poets and painters and musicians also are so accustomed to put outside of them the idea of beauty, that it becomes a real external existence, a thing which they see with spiritual eyes and then describe to you, but by no means create, any more than we seem to create the ideas of table and forms and light, which we put together long ago. There is no scientific discoverer, no poet, no painter, no musician, who will not tell you that he found ready made his discovery or poem or picture - that it came to him from outside, and that he did not consciously create it from within”.
“Gli uomini di scienza hanno a che fare con concetti estremamente astratti e generali. Con il costante e uso e la familiarità, questi, e le relazioni tra di essi, diventano reali ed esterni proprio come i comuni oggetti dell’esperienza, e la percezione di nuove relazioni tra di essi è così rapida, la corrispondenza della mente alle circostanze esterne così grande, che si sviluppa un senso scientifico reale, con il quale le cose sono percepite così immediatamente e veramente così come io vi vedo ora. Anche i poeti e i pittori e i musicisti sono così abituati a proiettare fuori di sé l’idea di bellezza, che diventa una reale esistenza esterna, una cosa che essi vedono con occhi spirituali e in seguito vi descrivono, ma che assolutamente non creano, non più di quando ci sembra di creare le idee di tavolo, di forme e di luce, che mettemmo insieme tanto tempo fa. Non esiste scopritore scientifico, poeta, pittore o musicista che non vi dirà di aver trovato già fatta la sua scoperta, la sua poesia o la sua pittura, che essa giunse a lui dall’esterno, e che non la creò consciamente dal proprio interno”.







Complimenti per l'interessante ed erudito articolo. Hai saputo raccontare con leggerezza e garbo un momento di storia della scienza e letteratura senza stancare, anzi, invogliando ad arrivare fino in fondo.
RispondiEliminaBuona giornata.
Massimo
Kees se scrivi così nessuno avrà il coraggio di commentare! E potrebbe insorgere anche l'invidia.
RispondiEliminaPerò, sudisfassiun, posso dire: io lo conosco, è mio 'mico!
Ma quante cose si imparano qui!!!! Un saluto.
RispondiEliminaGrazie dell'articolo. Molto molto interessante, come tutto questo blog.
RispondiEliminainteressantissimo blog!
RispondiEliminaUn articolo molto bello e interessante. Bisognerebbe parlare di più delle connessioni tra scienziati e il mondo della letteratura, in modo da recuperare la loro dimensione umana, troppo spesso dimenticata!
RispondiElimina