Poesia in forma di grafo

No, non in forma di rosa, proprio in forma di grafo. Un grafo G, che è una struttura matematica costituita da un insieme di elementi detti vertici o nodi collegati fra loro da archi o spigoli. I vertici sono in genere trattati come oggetti senza caratteristiche e indivisibili.

Un arco che ha due estremi coincidenti si dice cappio, mentre più archi che connettono gli stessi due estremi costituiscono un multiarco. Un grafo sprovvisto di cappi e di multiarchi si dice grafo semplice. In caso contrario si parla di multigrafo.

Un arco orientato è un arco caratterizzato da una direzione, indicata da una freccia che esce da un vertice e entra in un altro A seconda della presenza o meno di archi orientati, si distinguono i grafi orientati (o digrafi, grafi diretti) e i grafi non orientati. Un grafo semplice non contiene archi orientati.

Un percorso di lunghezza n in G è dato da una sequenza di vertici v₀, v₁,..., v_n (non necessariamente tutti distinti) e da una sequenza di archi che li collegano. I vertici v₀ e v_n si dicono estremi del percorso. Un percorso con gli spigoli a due a due distinti tra loro prende il nome di cammino. Un cammino chiuso (v₀ = v_n) si chiama circuito o ciclo. Un cammino in un grafo (orientato o non orientato) è detto hamiltoniano se esso tocca tutti i vertici del grafo una e una sola volta (figura a fianco). Un cammino viene invece detto euleriano quando tocca tutti gli archi del multigrafo una e una volta sola.

Un sottografo G’ è un grafo composto da un sottoinsieme dei nodi e degli archi di un grafo G più grande.

I grafi oggi sono tra i modelli più diffusi per rappresentare strutture sia naturali sia umane. Essi possono essere usati per modellizzare molti tipi di dinamiche delle relazioni e dei processi nei sistemi fisici, biologici e sociali. Molti problemi di interesse pratico possono essere affrontati mediante i grafi.

Nella informatica e nelle telecomunicazioni, i grafi sono usati per rappresentare e ottimizzare reti di comunicazione, organizzazione di dati, sistemi e algoritmi di calcolo, la struttura dei siti web, i motori di ricerca, ecc. La teoria dei grafi costituisce un'importante parte della combinatoria e trova largo utilizzo in topologia, nella teoria degli automi, nella geometria dei poliedri, nelle algebre di Lie, ecc. Essa è alla base di modelli di sistemi e processi studiati nell'ingegneria, nella fisica della materia condensata, nella chimica, nella biologia molecolare, nell’organizzazione aziendale, nella sociologia, nell’urbanistica, nello studio delle reti di traffico, nella linguistica strutturale, nella storia e nella filologia.

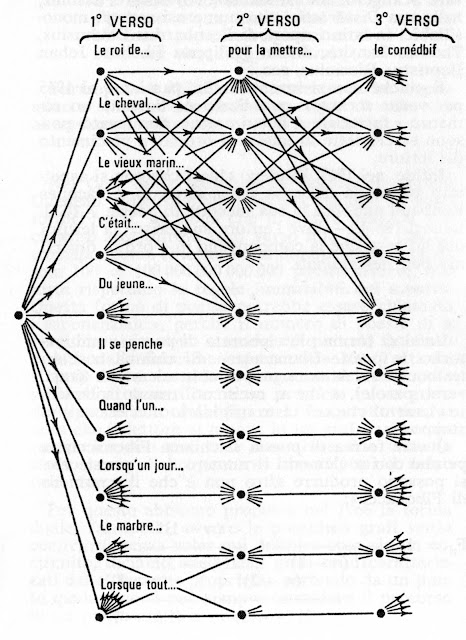
Come altre branche delle matematiche, la teoria dei grafi non poteva sfuggire all’attenzione dei membri dell’Oulipo, in particolare a quella di Claude Berge (1926-2002), uno dei fondatori del consorzio di letteratura potenziale nel 1960, che due anni prima aveva pubblicato il fondamentale Théorie des Graphes et ses Applications. Le opere letterarie basate sulla combinatoria, da quelle basate sui quadrati latini fino alle opere “esponenziali” come i Cent mille milliards de poèmes di Raymond Queneau, possono infatti essere rappresentate da grafi più o meno articolati (sotto è rappresentato il grafo semplificato dell'opera di Queneau) . Berge ha proposto nel 1966 il processo inverso, cioè creare, o ricreare, opere letterarie a partire dai grafi, applicando, per ovvi motivi, questo procedimento soprattutto alle poesie.

In questo contesto il grafo è necessariamente orientato, perché le frecce devono indicare l’ordine di lettura degli archi che rappresentano i versi dell’opera, che costituiscono un percorso dal vertice iniziale a quello finale che ad essa corrisponde. Inoltre il grafo non dovrebbe presentare circuiti, cioè cammini in cui il vertice iniziale e quello finale corrispondono. Detto in termini letterari, non si può incontrare due volte lo stesso verso in un percorso che rispetti il senso delle frecce. A meno che, voglio precisare, a meno che l’opera presenti più volte lo stesso verso!

Scegliendo opportunamente i versi, è possibile creare opere che possono essere lette a partire da un punto qualunque, e che possono terminare il percorso in un punto scelto a priori. In questo caso la struttura non può essere dettata da un grafo elementare, che limiterebbe considerevolmente le possibilità combinatorie, ma richiede un multigrafo con la possibilità di scegliere tra più archi quando si collegano talune coppie di vertici. È anche possibile considerare i sottografi dell’opera, in modo da ottenere poesie più corte, a patto di rispettare l’ordine delle frecce.

Così scrive Berge in Oulipo. La letteratura potenziale (Creazioni Ri–creazioni Ricreazioni), Clueb, Bologna, 1985: “Consideriamo l'esempio semplificato della figura.

I versi corrispondenti agli spigoli che arrivano allo stesso vertice (o che ne partono) sono stati scelti sulla base di una restrizione ben precisa; per esempio, quelli che arrivano al punto D contengono tutti la parola «uomo», quelli che ne partono hanno tutti la stessa struttura grammaticale, ecc... Di fronte a questa figura, il lettore può decidere in anticipo il punto di partenza e il punto di arrivo, e cercare il «percorso» più breve. Può anche formare delle «poesie hamiltoniane», corrispondenti a un percorso che incontri una volta e una volta soltanto ognuno dei vertici. Così il cammino hamiltoniano BADC da:

«No no, dice la signora offesa, io non sono sul punto di cercare l'uomo che sputi nella brocca».

Si possono anche formare delle poesie quasi euleriane, con percorsi che non passino per nessuno spigolo più di una volta e che utilizzino il massimo numero possibile di spigoli; basandosi semplicemente su concetti fondamentali, puramente matematici, della Teoria dei Grafi, si hanno così altrettanto restrizioni... e il numero dei testi che si possono ottenere partendo dalla stessa figura è infinito!”

Stimolato da questi esempi, ho deciso di utilizzare i grafi per il trattamento oulipiano di una poesia esistente, che ho scelto proprio perché presenta la ripetizione di due versi, giusto per dare un gusto ulteriore al mio esperimento. Si tratta di D’Autunno dello scrittore salisburghese Georg Trakl (1887–1914), grande figura dell'ambiente che cantò la Finis Austriae e fu tra i primi a incarnare, nella vita e nell’opera, la solitudine e la disgregazione dell’individuo nell’era contemporanea, sempre più isolato rispetto ai suoi simili.

D’Autunno comparve in Gedichte, l’unica raccolta di poesie pubblicata da Trakl quando era ancora in vita, nel 1913. L’anno successivo, sconvolto dall’esperienza di ufficiale medico durante la Grande Guerra (era laureato in farmacia) si sarebbe suicidato a Cracovia con un’overdose di cocaina. Riporto l’opera nella traduzione che fece Ervino Pocar per l’edizione che comparve per la BUR nel 1974, scusandomi di aver numerato i versi ai fini del mio esperimento:

01. I girasoli sulla siepe splendono,

02. Gl’infermi stan seduti, zitti, al sole.

03. Donne faticano nel campo e cantano,

04. Suonano le campane del convento.

05. Dicon gli uccelli favole remote,

06. Suonano le campane del convento.

07. Da presso note di violino giungono.

08. Si pigia oggi nei tini l’uva bruna.

09. Ora l'uomo si mostra lieto ed ilare.

10. Si pigia oggi nei tini l’uva bruna.

11. Sono aperte le camere mortuarie

12. Bell’e dipinte dal fulgor del sole.

Una semplice rappresentazione del testo con un multigrafo può essere la seguente, dove i dodici versi, rappresentati dagli archi numerati, collegano i vertici da A ad I. Il verso 04 è ripetuto nel verso 06, così come lo 08 è ripetuto al 10, perciò tra D ed E e tra F e G esistono frecce che tornano indietro rispetto al percorso di lettura considerato normale. Ciò nonostante, il grafo può essere rappresentato su un piano, senza che si abbiano incroci tra gli archi.

Esistono invece grafi nei quali sono presenti coppie di archi che si intersecano. Essi non possono essere disegnati nel piano senza evitare incroci tra gli archi. Questi grafi sono detti non planari, come ad esempio il grafo completo con 5 nodi, k₅ e il grafo bipartito completo con 3 + 3 nodi, k_3,3. Si tratta dei due grafi che il matematico polacco Kazimierz Kuratowski dimostrò nel 1929 essere i più semplici grafi non planari: un grafo è planare se e solo se non contiene alcun sottografo che sia omeomorfo a questi due. Il secondo grafo è abbastanza noto, perché rappresenta il gioco in cui viene chiesto di collegare le tre case (i vertici in alto) con ciascuno dei tre pozzi (i vertici in basso) con sentieri che si scopre non è possibile disegnare senza intersezioni.

Tornando alla poesia, ho rappresentato il testo di Trakl anche con un multigrafo nel quale ho ridotto il numero di vertici da 9 a 5, mantenendo ovviamente inalterato il numero degli archi a 12 (come i versi). Si tratta anche in questo caso di un grafo planare (l’arco 12 può essere disegnato fuori dal pentagono in modo che non incroci altri archi), nel quale è possibile leggere per intero il testo seguendo il percorso indicato dalle frecce da 1 a 12.

Così concepito, il multigrafo offre alcune interessanti possibilità combinatorie dal punto di vista letterario. Ad esempio è possibile considerare percorsi lungo i suoi sottografi, come ad esempio quello che è composto dai vertici CEAB (versi 11, 7, 1):

Sono aperte le camere mortuarie:

da presso note di violino giungono.

I girasoli sulla siepe splendono.

Oppure si può considerare il cammino hamiltoniano ABCDE (versi 1, 2, 3, 4, 7):

I girasoli sulla siepe splendono,

Gl’infermi stan seduti, zitti, al sole.

Donne faticano nel campo e cantano,

Suonano le campane del convento.

Da presso note di violino giungono.

Il lettore può divertirsi a trovare altri percorsi consentiti dagli archi orientati, oppure può creare un grafo per esplorare oulipianamente le possibilità offerte da una poesia di sua scelta.

(I due grafi relativi a D’Autunno sono stati disegnati con il programma che ho trovato qui).