Autoritratto della radice di 2

Il mio lavoro consiste nell’essere estratta ed esibita. Nell’essere estratta con il maggior numero di decimali possibile. È un lavoro da numero. Prima di tutto perché, quando si incontrano le matematiche, il numero ha voglia di mostrare loro i suoi decimali, poi perché, quando ci sono tanti numeri, essi vogliono far vedere più decimali degli altri. 

Un lavoro irrazionale. 

Io sono la radice quadrata di 2. 

C’è stato 1, 2, molti, poi c’è stato 3 e 4 e molti altri e adesso ci sono io. Sono il primo numero di cui è stata dimostrata l’irrazionalità e, alla prossima occasione, sarò dichiarato il più bello dei numeri irrazionali. 

Sono il numero più celebrato della schiera, quello al quale si sono interessati i più grandi, Euclide e Teeteto, Pitagora e persino Platone, e la mia condizione consiste nell’essere provato irrazionale. Tutti i matematici sanno dimostrare la mia irrazionalità. 

Essere un numero irrazionale è prima di tutto essere un numero diverso, tale da seminare l’inquietudine e il dubbio. 

Fare paura. Arrivare sulla scena in maniera tale che ti credono innocente, un semplice tratto in un quadrato (1), fino a che uno si turba perché tu non puoi esistere. 1, 2, va bene, 1,5 va bene lo stesso, ma non tu, fino a che delle infinità di numeri irrazionali vengono a copiarti. 

Nella vita di un numero non c’è il Terzo Stato: se non sei una frazione, allora sei irrazionale, e buonanotte al secchio! 

Le frazioni sono arrivate per dividere i numeri interi e, appena qualche secolo più tardi, tutti i matematici le usavano. 

Adesso ci sono io. 

Essere un numero irrazionale è una condizione che richiede un dono assoluto di se stessi e una dimostrazione rigorosa. Sono un numero irrazionale a tempo pieno. Lo sono per considerazione delle valutazioni 2-adiche del mio numeratore e del mio denominatore (2), cosa che fa sorridere i matematici esordienti. Lo sono per assurdo: se fossi una frazione irriducibile, il mio numeratore sarebbe pari e il mio denominatore anche (3), fatto che tormenta i miei appassionati. 

Prendete due numeri con i quadrati uguali, scriveteli uno accanto all’altro, sono sempre io che mi chiamo radice di 2, perché sono io ad essere il più positivo. 

Le costruzioni con riga e compasso, un quadrato doppio di un altro, li subisco mille volte alla settimana, i fogli di carta, ognuno la metà della superficie del precedente (4) e ciò nonostante esattamente della stessa forma, io li piego ogni sera prima di andare a letto presto. Conosco a memoria le mie approssimazioni per ridotte successive (5) e, quando chiudo gli occhi, vedo i miei decimali passare al rallentatore. 

Mi preparo anche ad affrontare quegli argomenti muti e insipidi che certi matematici utilizzano per dimostrare sia la mia irrazionalità sia la loro pedanteria, imponendomi delle dimostrazioni di quattro pagine quando sono sufficienti quattro righe o una figura. 

Tutto conta nella tua carriera. 

Un giorno l’essenziale diventa l’infinitezza del tuo sviluppo decimale. Tu hai limato l’argomento e hai finito per piantarti per aver dimenticato di segnalare l’assenza di periodicità in questo sviluppo. Hai sostenuto perentoriamente che bastava l’infinitezza, e hai perduto la faccia mostrando solamente che non eri decimale. 

Quando dormo, sono irrazionale, quando penso che il mio quadrato è uguale a 2, sono irrazionale. Vedo convergere verso di me delle moltitudini di metodi di Newton (6). La testa del mio 2 si piega sotto l’asticella del segno di radice, sento in tutto il mio essere l’irrazionalità di questa posizione. 

Quando nella sala rotonda del Palazzo della scoperta si parla d’irrazionalità, sono io ad essere citato per primo, e si liberano così tonnellate di decimali. Poi, le domande convergono sull’appariscente, il sedicente numero aureo che serve a contare le coniglie (7), gli sguardi si smarriscono verso i decimali allineati sui muri, e non rimane che un primo numero irrazionale, che serve ormai solo a presentare gli altri. 

È la regola. 

E poi, c’è il momento che arriva per forza in una vita, il solo momento di vero riposo, di riposo assoluto. Il riposo del primo numero irrazionale. 

Ti hanno presentato con rigore, come numero positivo il cui quadrato è 2, ti hanno provato non decimale, non razionale, hanno ricordato l’antiferesi (8), hanno evocato la geometria, hanno chiamato alla tua riscossa i vecchi signori barbuti, hanno invocato il sempre giovane e glabro Évariste Galois, considerandoti per dare un esempio, il primo esempio, di gruppo di Galois, e tu ti sei soddisfatto d’essere ancora una volta il primo, commettendo così lo stupido errore (che non è di distrazione perché le radici, anche loro, non conoscono la distrazione) di dimenticare che si è primi solo se esiste un secondo e tutta una sfilza di concorrenti, dopo i quali ti possono opporre un numero trascendente, un miserabile numero del quale tutti i decimali sono più o meno nulli (9), poi molti numeri trascendenti (10), poi non si parlerà più dei tuoi decimali se non per spiegare fino a che punto quelli di π sono più inattesi, più ricchi, più fantasiosi. E là è il vero riposo, il riposo infinito. Tu non sei trascendente, e, ancor peggio, il tuo sviluppo in frazione continua è periodico (11). Niente più importa, non sei più il divo dei numeri, la tua estensione è quadratica (senza parlare di quella dei tuoi muscoli, che si lascia andare), sai che diventerai il primo, ma il primo, volgare, numero algebrico.

-----OO---OO-----

Michèle Audin è docente di matematica all’Università di Strasburgo e, dal 2009, membro dell’Oulipo.  Questo autoritratto di è comparso un paio d’anni fa sul bellissimo sito Images des Mathématiques, ospitato dal CNRS (Centre National de la Recherche Scientifique).  

La Audin ha pubblicato questo autoritratto, assieme a quello della trottola, sul volume collettivo degli oulipiani C’est un métier d’homme, pubblicato da Mille et une nuits, che contiene una ventina di autoritratti assurdi o parodistici ispirati da un breve racconto di Paul Fournel intitolato “Autoritratto del discesista”. 

I fecondi rapporti tra matematica e letteratura esistenti in Francia sono testimoniati anche da un libro interamente dedicato da Ludmila Duchêne e Agnès Leblanc alla radice di due, Rationnel mon Q (Éditions Hermann), dal titolo deliziosamente ambiguo dal punto di vista fonetico. Si tratta di 65 “esercizi di stile” alla maniera di Queneau, in cui l’irrazionalità di viene dimostrata nello stile di Abel, Bourbaki, Lewis Carroll, Euclide, Fellini, Goldbach, Hitchcock, Idéfix, Kafka, François Le Lionnais, Mersenne, Ohm, Perec, Queneau, Racine, Stokes, Talete, Zazie, e molti altri. Ecco un esempio: 

ANGLICISMES

Proposichieune. La scouère route de 2 est un neummbeur irrachionneul. Prouf. Par l’abzeurde. Sinon la scouère route de 2 canne bi ritteune p/q ouère p et q sont deux neummbeurse entiers, praillemeu entre eux. On élève au scouère et alors on sie que p est divisibeule baille tou, et donc que q est divisibeule baille tou iota. Contradikchieune. 

Proposiscion. La radice squere di 2 è un irrascional namber. Prouf. Per abserd. Consider la radice squere di 2, ke can bi vritten p/q, uere p e q sono due nambers interi, irreeduchibilee tra di loro. Si eleva a squere e cosii si vedi che p è divisibol bai ciu. E cosii che q è  divisibol  bai ciu tuu. Contradiscion (3). 

Note 

1. 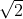è il primo numero irrazionale conosciuto, ottenuto come lunghezza delle diagonali di un quadrato di lato 1. 

2. Qui si va sul difficile, per cui mi limito a un collage di concetti tratti da Wikipedia in francese, sperando di dare un’idea della cosa. Nella teoria dei numeri, se p è numero primo, un numero p-adico è un oggetto che si può concepire come una sequenza di cifre in base p, eventualmente infinita a sinistra della virgola (ma sempre finita a destra della virgola). Con un’addizione e una moltiplicazione, che si calcolano come per i numeri decimali consueti, l’insieme dei numeri p-adici forma un corpo commutativo scritto . L'equazione su non ha soluzione, in quanto la valutazione p-adica del primo membro è pari mentre quella del secondo membro è dispari. D'altra parte, è un'estensione di , quindi, se l'equazione non ha soluzioni in , non ha neanche soluzioni in e è irrazionale. 

3. Se si potesse scrivere la frazione irriducibile , che non si può semplificare, allora, elevando al quadrato, si avrebbe . Allora , dove p sarebbe un numero pari e sarebbe divisibile per 4, quindi q sarebbe pari, in contraddizione con il fatto che la frazione deve essere irriducibile. Si tratta di una dimostrazione per assurdo. 

4. I formati dei fogli A della norme ISO 216, sono concepiti in modo che, se si taglia il foglio per la larghezza, si ottengono due fogli simili all’originale, cioè con lo stesso rapporto lunghezza/larghezza. Questo rapporto vale circa . 

5. Si tratta delle ridotte dello sviluppo di una frazione continua. Vedi nota n. 11. 

6. In analisi numerica, il metodo di Newton, chiamato anche metodo delle tangenti, è uno dei metodi per il calcolo approssimato di una soluzione di un'equazione della forma . Esso si applica dopo avere determinato un intervallo [a,b] che contiene una sola radice. 

7. Il riferimento è alla successione di Fibonacci, nata dall’intento di trovare una legge matematica che potesse descrivere la crescita di una popolazione di conigli individuando e registrandone la ragione quantitativa di incremento. La successione gode della proprietà per la quale il rapporto tra un termine e il suo precedente, tende al valore della sezione aurea, o phi, al tendere di n all'infinito. 

8. I greci chiamavano antiferesi l’algoritmo di approssimazione di una radice. 

9. Il testo allude all’esistenza di numeri trascendenti costruiti grazie al loro sviluppo decimale, come ad esempio il numero: 

 costruito da Joseph Liouville nel 1844, in cui tutti i decimali sono nulli tranne quelli di rango n! (il che causa tanti 0, sempre di più mentre si procede). 

10. I numeri algebrici sono quelli, reali o complessi, che costituiscono delle soluzioni di un’equazione polinomiale con coefficienti razionali, come . I numeri trascendenti sono i numeri irrazionali non algebrici, come ad esempio π. 

11. L’approssimazione di è legata allo sviluppo della frazione continua periodica: