La spiegazione secondo Wikipedia è che, “Nel passato 1 era a volte considerato un numero primo: ad esempio Derrick Norman Lehmer lo incluse nella sua tavola dei numeri primi pubblicata nel 1914. Oggi tuttavia si preferisce escluderlo, in quanto il suo inserimento tra i primi costringerebbe a riformulare in maniera più complessa diversi teoremi (come il teorema fondamentale dell'aritmetica) per tenere conto di questo caso speciale”.
Infatti il teorema fondamentale dell'aritmetica sostiene che ogni numero naturale maggiore di 1 o è un numero primo o si può esprimere come prodotto di numeri primi. La scomposizione in fattori primi di un numero n è unica, se si prescinde dall'ordine in cui compaiono i fattori. “È per garantire l'unicità della fattorizzazione che il numero 1 non viene considerato primo; se 1 fosse primo, ogni numero avrebbe infinite fattorizzazioni diverse. Per esempio: 10 potrebbe essere scritto come 5×2, ma anche come 5×2×1, o ancora 5×2×1×1×...×1; in questo modo la proprietà di unicità non sarebbe rispettata”.
Insomma, 1 non è più il primo numero primo, tuttavia nel passato furono date risposte diverse alla domanda del titolo. In effetti, per trovare il primo numero primo bisogna anche sapere qual è il primo numero naturale, e la risposta non è stata sempre univoca. La storia della primalità di 1 è interessante da ripercorrere, perché è anche un piccolo compendio della storia della matematica.
Prima di cominciare bisogna però precisare due cose. La prima è che stabilire se un numero (specialmente l’unità) è primo è una questione di definizione, scelta, contesto e tradizione, non di dimostrazione. Ciò nonostante, le definizioni non sono fatte a caso: esse sono legate all'uso che si fa della matematica e, specialmente in questo caso, della notazione usata. Ad esempio, man mano che l’uso dei numeri è cambiato, l’uno (l’unità, la monade), che all’inizio non era generalmente considerato un numero dagli antichi greci, è diventato un numero solamente duemila anni più tardi. Per gran parte del tempo non aveva senso chiedersi se 1 era un numero primo.
La seconda è che, quando ci atteniamo ai (moderni) interi positivi, non è difficile adattare i nostri teoremi per consentire al numero uno di essere considerato primo. Ad esempio, se si considera quanto dice Wikipedia sul fatto che l’unità è esclusa dal novero dei primi per preservare l’unicità della fattorizzazione, è anche vero che, nel passato, i matematici che definirono l’1 come primo non fecero altro che aggiungere poche parole al teorema fondamentale dell'aritmetica (TFA). Alla versione canonica del TFA è sufficiente aggiungere due caratteri (in rosso):
Teorema – Per ogni numero naturale n esiste un’unica fattorizzazione,
dove gli esponenti a sono interi positivi e
Nei primi tempi dello studio dei numeri primi, quelli ad esempio di Euclide, l’unità (uno) non era considerata un numero, così era automaticamente esclusa dal novero dei primi. Nel libro 7 degli Elementi, Euclide dava queste definizioni:
− Una unità è ciò per cui ogni singola cosa che esiste è chiamata uno.
− Un numero è una moltitudine composta da unità.
− Un numero primo è quello che è misurato soltanto dall'unità.
− I numeri primi tra loro sono quelli che sono misurati soltanto dall'unità come misura comune.
− Un numero composto è quello che è misurato da qualche numero.
Euclide (con i suoi contemporanei) non aveva bisogno di dire esplicitamente che l’unità non era un numero primo, perché i primi erano una sottocategoria dei numeri, mentre uno non era un numero. La sequenza dei numeri primi iniziava pertanto con il due. Su questo fatto concordavano anche Aristotele e Teone di Smirne (nel primo libro della Matematica utile per comprendere Platone), con piccole differenze di termini. Escludere l’1 dai numeri pare proprio una regola costante, anche se, come tutte le regole, c’è un’eccezione. Speusippo (IV sec. a C.), nipote di Platone e successore dello zio come scolarca dell’Accademia di Atene, il cui pensiero ci è giunto in frammenti e attraverso ciò che scrisse di lui Diogene Laerzio, non solo considerava l’unità come un numero, ma la indicava come primo.
Gli scrittori che si occuparono della questione nella tarda antichità concordano nel considerare i numeri primi un sottoinsieme dei numeri dispari, escludendo sia l’uno che il due dal loro novero: per loro il primo numero primo era il tre. Severino Boezio (475-525) scrisse attorno al 505 il De institutione arithmetica, in cui viene illustrato l’aspetto peculiare dell’unità: poiché ciascun numero
è preceduto e seguito da due numeri, la cui semisomma è pari al numero stesso, solo l’uno fa eccezione, dal momento che ha un solo termine accanto a sé, il due, di cui è la metà. Come si può vedere, lo zero non è minimamente contemplato.
Quasi contemporaneo gli fu Marziano Capella, vissuto tra IV e V secolo, pagano e pitagorico, che nell’opera De nuptiis Philologiae et Mercurii, una specie di enciclopedia dell’erudizione classica diffusissima nel Medioevo cristiano, riassume come segue le proprietà dei primi numeri naturali:
“Abbiamo succintamente discusso i numeri che comprendono le prime serie, le divinità a loro assegnate, e la virtù di ciascun numero: Ora indicherò brevemente la natura del numero stesso, quali relazioni esistono tra gli uni e gli altri, e quali forme essi rappresentano (…): la monade non è un numero, la diade è un numero pari, la triade è un numero primo, sia per ordine sia per proprietà; la tetrade appartiene in pari volte alla classe pari, la pentade è primo (…)”
Nel terzo dei 20 libri delle Etymologiae o Origines, quello intitolato De quatuor disciplinis mathematicis, Isidoro di Siviglia (c. 560-636), dopo aver spiegato il significato della parola aritmetica: “L’aritmetica è la disciplina dei numeri. I Greci chiamano il numero arithmòn”, fornisce una definizione di numero, accompagnata da una delle sue fantasiose paraetimologie: “Numero è una moltitudine costituita di unità. Infatti uno è il seme del numero, ma non un numero. Nummus (moneta) ha dato il suo nome a numerus, e per la frequenza del suo uso ha dato origine alla parola”. Naturalmente non si pone il problema se l’unità possa essere un numero primo.
Le cose incominciarono a cambiare solamente secoli dopo, quando Simon Stevin (Stevino) nel 1585 introdusse una nuova notazione per i numeri decimali, che permetteva di estendere a tali numeri le normali operazioni algebriche sui numeri interi, anziché usare la notazione frazionaria utilizzata fino ad allora. Egli poneva le basi per l’introduzione dell’insieme R dei numeri reali e, per quanto riguarda l’1, evidenziava come non esistesse differenza notazionale o algoritmica tra esso e gli altri numeri.
I cambiamenti tuttavia avvennero con lentezza, e circa un secolo più tardi, Joseph Moxon, l’autore di Mathematicks made easie, or, A mathematical dictionary explaining the terms of art and difficult phrases used in arithmetick, geometry, astronomy, astrology, and other mathematical sciences, il primo dizionario matematico in lingua inglese, pubblicato postumo nel 1700, affrontava la questione se uno fosse un numero in modo problematico.
Alla voce “Numero”, Moxon afferma che Uno è comunemente considerato l’origine dei numeri e pertanto non è propriamente un numero. “Tuttavia confesso che ciò (per quanto generalmente accettato) ad alcuni sembra contestabile, perché contro di esso si potrebbe argomentare: una Parte è della stessa natura di ciò che è il suo Intero; un’unità è parte di una moltitudine di numeri; pertanto un’Unità è della stessa natura di una moltitudine di Unità: ma la natura e sostanza dei Numeri è l’Unità; pertanto la sostanza di un’Unità è il Numero. Oppure così: dato un Numero, se dallo stesso si sottrae 0 (nessun Numero), il numero dato rimane invariato: sia 3 il numero dato, e da esso si sottragga 1, ovvero l’Unità (che, come essi dicono non è un Numero), allora il Numero dato, diciamo 3, rimane invariato, il che è assurdo (…)”.
La ridefinizione dell’unità come numero fece diventare ragionevole la domanda se esso fosse un numero primo, tuttavia il modo in cui si utilizzavano allora i numeri primi non spinse verso alcuna particolare definizione. La fattorizzazione non era ancora vista come argomento d’interesse in se stessa, ma solo come un metodo per trovare i divisori.
Iniziò allora un periodo confuso, in cui alcuni sostenevano che l’unità non era un numero primo e altri che lo era. Tra i primi si possono citare Mersenne (1625), van Schooten (1657) e Eulero (1770), mentre tra i secondi c’erano Wallis (1685), Prestet (1689), Lambert (1770, Felkel (1776) e Waring (1782). Christian Goldbach (1690 –1764), nell’esporre in una lettera a Eulero del 1742 la sua famosa congettura che ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi (che possono essere anche uguali), dà per scontato che 1 sia un numero primo. Sembra strano che nessuno si chiedesse se le fattorizzazioni fossero uniche, un concetto che con il senno di poi sembra oggi così ovvio. Comunque i tempi erano maturi perché Carl Friedrich Gauss si mettesse al lavoro.
Quando, nel 1801, Gauss per primo stabilì e dimostrò parzialmente il TFA nelle Disquisitiones Arithmeticae, non solo aprì la strada per far sì che la fattorizzazione unica sia centrale nella comprensione dei numeri interi, ma discusse una generalizzazione degli interi estendendoli al campo complesso (interi di Gauss), che rese i matematici assai più attenti al ruolo dell’unità nelle fattorizzazioni. Nel testo Gauss non definiva i numeri primi esplicitamente, ma forniva un argomento fondamentale per la loro moderna definizione.
L’opera del Princeps mathematicorum costituì un vero e proprio spartiacque nella definizione di un numero come primo, ma i matematici incominciarono a convenire solo molto lentamente attorno alla moderna definizione, che esclude l’unità. In molti continuarono a considerare l’unità un numero primo, tra di essi Legendre (1830), Weierstrass (1876), Cayley (1890), Klein (1897), Kronecker (1901) e Lehmer (1914). D’altra parte cresceva il numero di chi la escludeva, come Barlow (1811), Reynaud (1835) Dirichlet (1863), Meissel (1870), Chebyshev (1889), Lucas (1891), Landau (1909) e von Mangoldt (1912).
Uno sguardo alle varie edizioni della Enciclopædia Britannica pubblicate nei due decenni a cavallo del 1900 conferma questa diversità di vedute. Capita addirittura che lo stesso autore (ad esempio Arthur Cayley, ma non è il solo) consideri l’unità un numero primo in un articolo e poi la escluda in un altro della stessa edizione, a dimostrazione del fatto che spesso l’uso determina la definizione. I compilatori di tavole dei numeri primi furono i più restii ad escludere l’1 dalla sequenza, convinti che un numero possa essere solamente primo (compresa l’unità) oppure composto. Fu questa la ragione dell’inclusione di uno nella storica tavola dei numeri primi di Lehmer pubblicata nel 1914, che la sequenza OEIS A008578 ripropone.
L’ultimo grande matematico a considerare il numero 1 come primo fu G. H. Hardy, che lo incluse nelle prime sei edizioni (dal 1908 al 1933) del suo testo A Course of Pure Mathematics. Hardy presentava la dimostrazione di Euclide che esistono infiniti numeri primi con una sequenza che iniziava con l’1:
“La dimostrazione di Euclide è la seguente. Ammettiamo che esista solo un numero finito di primi, siano essi 1, 2, 3, 5, 7, 11, … n. Consideriamo il numero 1 + (1× 2×3×5×7×11, … n). Tale numero non è evidentemente divisibile da nessuno dei numeri 2, 3, 5, 7, 11, … n, poiché il resto, diviso da uno qualsiasi di questi numeri è 1. Esso non è pertanto divisibile da alcun primo tranne 1, ed è esso stesso primo, che è contrario alla nostra ipotesi”.
Nella settima edizione, del 1938, questa dimostrazione fu riscritta, in modo che il primo numero primo fosse il 2:
“La dimostrazione di Euclide è la seguente. Siano 2, 3, 5, … pn tutti i numeri primi fino a pn e sia P = (2×3×5 … pn) + 1. Allora P non è divisibile da nessuno dei numeri 2, 3, 5, … pn. Quindi o P è primo, o P è divisibile da un primo p compreso tra pn e P. In entrambi i casi esiste un primo più grande che pn, e quindi un’infinità di primi”.
Eppure ci sono ancora moltissimi testi scolastici che quasi novant’anni dopo considerano 1 un numero primo. Boh.
Caldwell, Chris K.; Xiong Yeng (2012). What Is The Smallest Prime? ArXiv: 1209.2007v2
Caldwell, Chris K.; Xiong Yeng (2012). What Is The Smallest Prime? ArXiv: 1209.2007v2


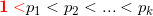









Primo!(A commentare).
RispondiEliminaComplimenti per l'articolo: finalmente ho capito chi è il "primus - non - inter pares".
Articolo interessantissimo: da una domanda apparentemente semplice, è venuta fuori una bella "cavalcata" storico/matematica.
RispondiEliminaGrazie. Un saluto
Marco
Per me l'1 è primo. E faccio notare che, in questa ipotesi,
RispondiEliminail primo numero è primo,
il secondo numero è primo,
il terzo numero è primo,
il quarto numero NON è primo,
ma non è neanche ultimo.
awesome
RispondiEliminaGrazie di cuore, collega anonimo! voglio aggiungerti altre incontrovertibili affermazioni, fra cui:
RispondiElimina-Tutti i numeri divisi per se stessi danno UNO, tranne lo ZERO, che dà "error".
-Tutti i numeri moltiplicati per UNO danno se stessi, tranne l'UNO, che dà quell'altro UNO.
-(corollario) Ogni numero meno se stesso da zero, tranne lo zero, che dà se stesso.
Un Ingegnere un Fisico e un Matematico vengono coinvolti in una ricerca per verificare se è corretta l'asserzione "tutti i numeri dispari sono primi"
RispondiEliminaInizia il Matematico:
"uno è primo, tre è primo, cinque è primo, sette è primo, nove NON è primo
==> l'asserzione è falsa"
Il Fisico:
"uno è primo, tre è primo, cinque è primo, sette è primo, nove NON è primo, undici è primo, tredici è primo...
==> l'asserzione è vera, salvo alcune incertezze di misura"
L'Ingegnere:
"uno è primo, tre è primo, cinque è primo, sette è primo, nove è primo, undici è primo, tredici è primo...
==> l'asserzione è vera!"
Amo le barzellette sugli ingegneri.
RispondiEliminaMa, da ingegnere, posso assicurarti che questa era una barzelletta sui numeri dispari.
EliminaO sui numeri primi.
Tanto è lo stesso.
Dott. Ing. Nonimo A.
E così l'1 per così tanto tempo non è stato un numero... ti son debitore di una nuova (ennesima) interessantissima scoperta.
RispondiEliminaL'immagine dove si cita Gauss si riferisce a partizioni, non fattorizzazioni... sbaglio?
RispondiEliminaL'immagine è un frammento della lettera di Goldbach a Eulero del 1742. Si tratta ovviamente di partizioni.
Elimina