La principessa Hoppy, una favola matematica

In quei tempi la principessa aveva un cane e quattro zii che erano re.

Il primo re si chiamava Aligoté. Era il re dello Zambesi e dei dintorni.

Il secondo re si chiamava Babylas. Era il re di Ipermetrope e dei dintorni.

Il terzo re si chiamava Eleonor (senza a) e il quarto Imogene.

Anche Eleonor (senza a) e Imogene erano re di qualcosa. Avevano ciascuno un regno molto grande e bello, ma il racconto ora non dice dove per motivi di sicurezza.

Il racconto dice quello che ci vuole quando ci vuole e il racconto ora dice che Aligoté faceva talvolta visita a Babylas nel suo regno, oppure a Eleonor nel suo, o ancora a Imogene nel suo, e il racconto dice che forse capitava che Babylas facesse talvolta visita a Eleonor nel suo regno, oppure a Imogene nel suo, o ancora a Aligoté, e il racconto dice che capitava che Eleonor facesse talvolta visita a Imogene nel suo regno, oppure a Aligoté nel suo, o ancora a Babylas, che Imogene qualche volta andasse a visitare Aligoté nel suo regno, a Babylas nel suo, o ancora a Eleonor. Almeno così dice il racconto.

E quando il re Aligoté si trovava dal re Babylas con la principessa e il suo cane e la principessa era scesa a giocare con la palla con il suo cane sul prato in fondo alla scalinata, il re Babylas disse ad Aligoté: – “Mio caro cugino, se passassimo nel mio ufficio”. Ma qui il racconto cessa di parlare di Aligoté e di Babylas e torna a Eleonor che è andato a visitare Imogene nel suo regno.

E il racconto dice che quando il re Eleonor si trovava da Imogene con la principessa e il suo cane e la principessa era scesa a giocare con la palla con il suo cane sul prato in fondo alla scalinata, il re Imogene disse a Eleonor: – “Mio caro cugino, se passassimo nel mio ufficio”. E quando Eleonor e Imogene stavano seduti entrambi nell’ufficio e avevano chiuso a chiave, i due complottavano.

Bisogna dirvi che ai quei tempi la principessa aveva molte preoccupazioni. Perché, ogni volta che uno dei quattro re suoi zii (per esempio Aligoté) rendeva visita a un altro dei suoi quattro zii (per esempio Imogene) nel suo regno e che entravano nell’ufficio dopo averla mandata a giocare con la palla con il suo cane sul prato in fondo alla scalinata e chiudevano a chiave, essi complottavano.

Complottavano contro uno dei quattro re che erano i suoi quattro zii! E per di più, non era raro che uno dei re (per esempio Eleonor), si facesse visita da solo nel suo regno, accompagnato dalla principessa e dal cane, e dopo aver mandato la principessa a giocare con la palla si chiudeva a chiave nel suo ufficio con se stesso per complottare. Si facevano molti complotti e il cane ne aveva le scatole piene di giocare con la palla.

Il racconto ricorda qui che quando il re Utherpendragon si trovava colpito dal male della morte, fece chiamare presso di sé la principessa e il suo cane e anche i suoi quattro nipoti Imogene, Aligoté, Babylas, Eleonor (senza a) e disse loro:

“Figli miei, figlia mia, mio cane, so che sto per morire. Ho il male della morte e ciò non perdona. Quando sarò morto, – aggiunse girandosi verso i quattro re suoi nipoti, – so bene ciò che succederà. Imogene, per esempio, andrà a fare visita a Babylas nel suo regno, con la principessa e il suo cane, e che cosa faranno? ve lo dirò. Manderanno la principessa a giocare con la palla con il suo cane sul prato in fondo alla scalinata, entreranno nell’ufficio, chiuderanno a chiave e complotteranno. Contro chi? Non lo so, me ne frego e mi lascia indifferente. OK, non posso impedirvelo. Ho il male della morte, sto per crepare, Merlino m’ha detto che non c’è niente da fare. Ma c’è una regola sacra che in tempi immemorabili istituì San Benedetto e che voi mi giurerete di rispettare per complottare. OK?”

E Utherpendragon continuò con voce potente:

“Regola di San Benedetto:

Siano tre re tra voi quattro: il primo re, il secondo re e il terzo re.

Il primo re non ha importanza quale sia.

Il secondo re non ha importanza quale sia.

Il terzo re non ha importanza quale sia.

– “Il secondo re può essere lo stesso che il primo?”

– "Of course” disse Uther.

Allora:

Il re contro il quale complotta il primo re quando fa visita al re contro il quale complotta il secondo re quando fa visita al terzo deve essere esattamente lo stesso re contro il quale complotta il re contro il quale complotta il primo re quando fa visita al secondo, quando fa visita al terzo.

Ok disse Uther, non è tutto.

Quando un re farà visita a un altro re, essi complotteranno sempre contro lo stesso re. E se due re distinti rendono visita a uno stesso terzo, il primo non complotterà mai contro lo stesso re che il secondo. Contro ciascun re, infine, si complotterà almeno una volta all’anno nell’ufficio di ciascuno dei re.

Ho detto (disse Uther) OK? OK disse Uther e morì.

Il racconto dice ora che la principessa e il suo cane avrebbero volentieri voluto sapere contro chi complottava lo zio Imogene quando rendeva visita allo zio Babylas e si chiudevano a chiave nell’ufficio. E, in modo più generale, la principessa avrebbe volentieri voluto sapere se, dati due qualsiasi dei suoi zii, quello dei suoi zii contro il quale complottava il primo quando faceva visita al secondo era, oppure no, lo stesso contro il quale complottava il secondo quando faceva visita al primo.

“Sì” disse il cane.

Aveva preso la palla sul prato in fondo alla scalinata e la teneva, bavosa, tra i denti.

“Non parlare con la bocca piena” disse la principessa “e perché dici sì, di grazia?”

“Erché un gruo a uatro eleenti è neessariaente coutatiuo” disse il cane.

Era bravissimo in genere nella traduzione canino–francese quando aveva una palla tra i canini.

“Ah”, disse la principessa.

Era arrivato il momento di andare a far merenda ed essi risalirono in cucina dove li attendeva la regina Ingrid.

Ora, dice il racconto, i re Aligoté, Imogene, Babylas e Eleonor erano cugini di primo grado e avevano come mogli quattro cugine di primo grado.

Erano le regine Adirondac, Botswanna, Eleonora (con la a) e Ingrid. La regina Adirondac era figlia di Zibelina e Zanivcovetto. La regina Botswanna era figlia di Yolanda e Ygrometria. Le regine Eleonora (con la a) e Ingrid erano anche loro figlie, ma il racconto non dice di chi, per motivi di sicurezza.

Il racconto fila diritto verso la fine e dice che quando Aligoté per esempio faceva visita a Imogene con il solo scopo di complottare con lui secondo la regola di San Benedetto, la regina Adirondac faceva visita alla regina Ingrid nella sua cucina. E, mentre i re complottavano, le regine facevano la composta. Tanto e così bene che il re Aligoté andandosene poteva depositare alla posta un pacco contenente il resto di composta che non era stato mangiato nella merenda destinata alla regina che era la sposa del re contro il quale lo stesso pomeriggio nell’ufficio di Imogene aveva complottato.

Tutto andava per il meglio nei regni. I re complottavano, le regine compostavano, la principessa giocava con la palla con il suo cane sul prato tutto verde in fondo alla scalinata, il cane traduceva dal francese al canino e dal canino al francese, quando un mattino…

Esistono quadri il cui valore si rivela solo con l’aiuto di un commento o di un’analisi critica. Così capita anche per il racconto La principessa Hoppy o il racconto del Labrador, iniziato a scrivere nel 1972 da Jacques Roubaud, poeta e matematico membro del gruppo dell’Oulipo, pubblicato come n. 2 della Biblioteca Oulipiana nel 1974 ed edito in forma ampliata e definitiva nel 2008 dalle Editions Absalon con un lungo commento di spiegazione sulle sue implicazioni matematiche. Sì, perchè quella che all’inizio sembra una piacevole e bizzarra fiaba postmoderna di ambientazione medievale è in realtà una delle opere più sperimentali pensate all’interno dell’Oulipo, costruita attorno a numerose restrizioni formali, visibili ed invisibili. Il testo completo consta di 139 pagine ed è suddiviso in nove capitoli, ma qui ho tradotto la versione “di assaggio” scritta nel 2007 per essere rappresentata in uno spettacolo teatrale.

Nel racconto, che ha come protagonista la principessa Hoppy (il cui nome ricorda quello della tribù indiana degli Hopi), sempre intenta a giocare a palla con il suo cane sapiente e parlante, i suoi zii re sono costantemente impegnati a complottare, mentre le loro mogli sono affaccendate a preparare la composta («parce que les rois complotent sans elles – c’est à dire sans L», spiega l’autore con un calembour impossibile da tradurre, basato sulla somiglianza tra complotent e compôtent). Il cane della principessa è un labrador sapiente, il quale con lei parla il «canino comune», un francese appena comprensibile che obbedisce a una contrainte inventata da Perec che consiste nel ricorrere solo alle undici lettere (E S A R T I N U L O C) più utilizzate nella scrittura di tale lingua. Il cane conosce anche il «canino superiore», idioma che procede da una contrainte non ancora identificata nonostante i numerosi tentativi degli esperti. La principessa riceve a un certo punto la visita di un astronomo venuto da Bagdad e aiuta sua cugina a fare i compiti, compiti che vengono assegnati anche al lettore durante la narrazione e soprattutto nell’appendice, dove il cane erudito pone 79 quesiti di diversa difficoltà.

Se la genesi del racconto si basa sulla cifra 4 (i re, le regine, gli uffici, le cucine, ecc.) e sulla relazione «X e Y complottano contro Z», ispirata a Roubaud dall’analoga «X scambia Y per Z» utilizzata da Raymond Queneau, e se è altrettanto facile accorgersi come molte frasi sono costruite mediante la permutazione di elementi, è proprio il cane a indirizzare il lettore verso le strutture meno evidenti, quando pronuncia una frase in canino comune che interessa la matematica moderna. Egli dice infatti “Erché un gruo a uatro eleenti è neessariaente coutatiuo” (“Perché un gruppo a quattro elementi è necessariamente commutativo”), rivelando l’utilizzo di restrizioni formali prese a prestito dalla teoria degli insiemi e da quella dei gruppi (nello specifico il cane fa riferimento a un gruppo abeliano). Mi limito a considerare il concetto di relazione, anche se il discorso da fare sarebbe assai ampio, ma la lunghezza dell’articolo e la pazienza del lettore sono vincoli che voglio rispettare.

Consideriamo ad esempio i due insiemi A = {Aligoté, Imogene, Babylas, Eleonor} e B = {Adirondac, Botswanna, Eleonora, Ingrid}. È possibile collegare gli elementi di A (i re) con quelli di B (le regine) in modo che ad ogni elemento dell'insieme A corrisponda in B un elemento, sua moglie. In questo modo abbiamo messo in relazione elementi di A con quelli di B. Si sono così definiti:

- l'insieme A (o insieme di partenza, detto dominio)

- l'insieme B (o insieme di arrivo, detto codominio)

- una proprietà: "essere sposati" .

Ad esempio possono venire individuate le seguenti coppie ordinate: (Aligoté, Ingrid), (Eleonor, Adirondac), (Imogene, Botswanna), (Babylas, Eleonora). Nel dominio prendiamo sempre il primo elemento della coppia ordinata, nel codominio prendiamo il secondo elemento. La relazione R può essere definita dall'insieme delle coppie che sono associate tra di loro:

R = {(Aligoté, Ingrid), (Eleonor, Adirondac), (Imogene, Botswanna), (Babylas, Eleonora)}

Abbiamo in questo caso una corrispondenza biunivoca: ad ogni elemento di A corrisponde uno e un solo elemento di B, e viceversa.

Non è detto che i due insiemi considerati debbano avere lo stesso numero di elementi. Si può ad esempio considerare l’insieme A’ dei maschi (che coincide con quello dei re: A’≡A, formato da 4 elementi) e quello B’ delle femmine (che questa volta comprende anche la principessa Hoppy e ha 5 elementi, perciò B’ ≠ B). Se si investigasse allora la proprietà “essere zio di” si individuerebbero le coppie ordinate (Aligoté, Hoppy), (Eleonor, Hoppy), (Imogene, Hoppy), (Babylas, Hoppy) e la relazione sarebbe di natura differente (per i curiosi: una relazione funzionale, f : A→B).

Una relazione R tra due insiemi non vuoti A, B (che possono anche coincidere) è definita quando esiste un modo per associare a certi elementi di A elementi di B. Normalmente, per realizzare questa associazione viene data una proprietà, che indichiamo con r(x,y), tale che presi due elementi qualsiasi x (che appartengono ad A) ed y (che appartengono a B), si verifichi che la proprietà r(x,y) o è vera o è falsa. Ad esempio, tra tutte le possibili combinazioni di re (insieme A) e regine (insieme B), che i matematici chiamano prodotto cartesiano A × B, solo alcune di esse verificano la proprietà r(x,y) che x sia sposato a y, cioè che x sia in relazione con y (in simboli: xRy). Possiamo perciò dire che una relazione (l’insieme delle caselle con la crocetta) è un sottoinsieme del prodotto cartesiano A×B (tutte le caselle dello schema):

Se i due insiemi coincidono, si parla di relazioni in un insieme, per le quali valgono le stesse considerazioni fatte in precedenza. La relazione in questo caso è un sottoinsieme del prodotto cartesiano A × A. Sono relazioni in un insieme quelle che intercorrono tra i re che costituiscono l’insieme A, relazioni che possono essere di diverso tipo, ad esempio:

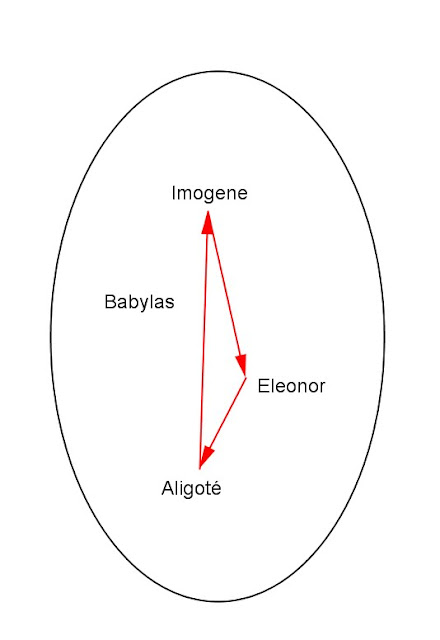
- Aligoté e Imogene complottano

- Babylas complotta contro Eleonor e Eleonor complotta contro Babylas (proprietà simmetrica):

- Aligoté complotta contro Babylas , ma Babylas non complotta contro Aligoté (proprietà antisimmetrica):

- Imogene complotta contro se stesso (proprietà riflessiva):

- Eleonor non complotta contro se stesso (proprietà antiriflessiva)

- Eleonor complotta con Aligoté, Aligoté complotta con Imogene, allora Eleonor complotta con Imogene (proprietà transitiva):

Mi fermo qui per motivi di sicurezza. Insomma, a ben vedere, La principessa Hoppy non è solo una favola bizzarra o, forse, è assai più bizzarra di quanto sembri.

Di Roubaud mi sono già occupato in Tre lettere di Jacques Roubaud.