Soluzione del Paradosso

Soluzione del Paradosso

Uno spettacolo per marionette filosofiche

di Abner Shimony

PERSONAGGI: Zenone, Allievo, il leone

SCENA: La scuola di Zenone a Elea

ALL.: Maestro! C’è un leone nelle strade!

ZEN.: Benissimo. Hai ben imparato la tua lezione di geografia. Il quindicesimo meridiano, misurato rispetto a Greenwich, coincide con la strada maestra dal tempio di Poseidone all’Agorà – ma non devi dimenticare che è una linea immaginaria.

ALL.: Oh, no, Maestro! Devo umilmente dissentire. Si tratta di un leone reale, un leone di serraglio sta venendo verso la scuola!

ZEN.: Ragazzo mio, nonostante il tuo profitto in geografia, che è a suo modo degno di lode – anche se essenzialmente l’arte del topografo è in realtà separata dal capello di un teodolite dall’abilità di uno schiavo – sei scarso in filosofia. Ciò che è reale non può essere immaginario, e ciò che è immaginario non può essere reale. L’essere è, e il non-essere non è, come ha dimostrato il mio riverito maestro Parmenide per primo, per ultimo e per sempre, e come ho cercato di trasmettervi.

ALL.: Perdonatemi, Maestro. Nella mia fretta e concitazione, esse stesse espressioni di passione non degna di voi e della nostra scuola, ho parlato oscuramente. Sono di nuovo caduto nell’abisso tra il pensiero e la parola, che, come ci avete insegnato, è la trappola allestita dal non-essere. Ciò che volevo dire è che un leone è fuggito dallo zoo, e con velocità deliberata sta filando in direzione della scuola e presto sarà qui!

Il leone compare da lontano.

ZEN.: Oh, ragazzo mio, ragazzo! Mi addolora contemplare l’impenetrabilità dell’umano intelletto e la sua incommensurabilità nei confronti del vero. Inoltre, ora riconosco che un noviziato di trent’anni è troppo breve – sub specie aeternitatis – e dev’essere aumentato a quaranta, prima che l’apprendistato vero e proprio possa iniziare. Un vero leone, forse,; ma che davvero stia correndo è impossibile; e che stia davvero venendo qui, è assurdo!

ALL.: Maestro…

ZEN.: Per poter correre dal giardino zoologico alla scuola eleatica, il leone avrebbe prima dovuto percorrere metà della distanza.

Il leone percorre metà della distanza.

ZEN.: Ma c’è una prima metà di quella metà, e una prima metà di quella metà, e poi ancora una prima metà di quella metà da percorrere. E così le metà devono per necessità regredire alla prima sillaba del tempo documentato – no, esse devono recedere ancora prima della prima sillaba. Per avere viaggiato solo la più piccola parte dell’intervallo dal giardino zoologico alla scuola, il leone sarebbe stato obbligato a intraprendere i suoi viaggi infinitamente tanto tempo fa.

Il leone fa irruzione nel cortile della scuola.

ALL.: Oh, Maestro, correte, correte! Ci è addosso!

ZEN.: E così, per reductio ad absurdum, abbiamo provato che il leone non avrebbe mai potuto aver iniziato il percorso, la cui mera illusione ti ha così indegnamente riempito di panico.

L’allievo sale su una colonna ionica, mente il leone divora Zenone.

ALL.: La mia mente è stordita. Come poteva esserci un difetto nel ragionamento del Maestro?

Da Zeno’s Paradoxes, editor Wesley C. Salmon, The Bobbs-Merrill Co., Indianapolis and New York, 1970.

Abner Shimony (1928) è un fisico quantistico e filosofo della scienza americano. Oggi è professore emerito all’Università di Boston. Shimony è noto per aver esteso l’ineguaglianza CHSH, forma empiricamente misurabile del teorema di Bell (nessuna teoria fisica a variabili locali nascoste può riprodurre le predizioni della meccanica quantistica). Dal 1992 ha proposto una misura geometrica dell’entaglement dei quark. Dal punto di vista epistemologico le sue ricerche hanno cercato di accostare in una “coesistenza pacifica” la meccanica quantistica e la relatività speciale. Come autore non professionale ha pubblicato Tibaldo and the Hole in the Calendar (1998), la storia della battaglia e delle strategie adottate da un ragazzino italiano di 11 anni per non perdere il suo tredicesimo compleanno quando il calendario gregoriano avrebbe sostituito quello giuliano nel 1582. Il libro è stato pubblicato anche in Italia (Tibaldo e il buco del calendario, Springer, 1999), ma è ormai fuori catalogo.

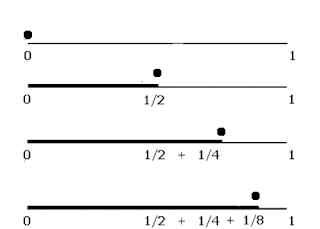
In questa sua simpatica versione del paradosso della dicotomia, che voleva mettere in evidenza l’impossibilità del movimento e addirittura il suo inizio, la soluzione è affidata alle fauci di un leone, che di paradossi non sembra interessarsi molto. In realtà sappiamo che il leone percorre la distanza dallo zoo alla scuola eleatica, che poniamo uguale a 1, percorrendo la seguente serie di segmenti:

che può essere formalizzata scrivendo la serie infinita (concetto che i greci non conoscevano o che li spaventava):

che converge proprio a 1, quindi il paradosso sembra non sussistere. Ma è proprio così?