Gabrio Piola, bigotto, reazionario e matematico sublime

 

Il sito di biografie dei matematici Mac Tutor dell’Università di St. Andrews, riferimento mondiale per lo studio della storia della disciplina, non riporta nulla sul matematico e patrizio milanese Gabrio Piola (1794-1850), eppure i suoi concittadini gli hanno dedicato una grande piazza, una fermata della metropolitana, la più vicina al Politecnico e a Città Studi, e una (contestata) statua nel cortile d’onore di Brera realizzata da Vincenzo Vela. Che Piola non fosse molto noto già pochi anni dopo la morte è dimostrato dalle polemiche che seguirono l’inaugurazione del monumento nel 1857: la stampa popolare parlò di “abuso di collocare in questo santuario di dottrina monumenti ad uomini di modestissima fama”. In un numero della rivista satirica milanese “L’Uomo di Pietra” pubblicato nello stesso anno compare una bellissima vignetta in cui la statua di Gabrio Piola è circondata dalle altre statue del cortile di Brera che cercano di consolarla perché, nel momento in cui fu presentata al pubblico, nessuno riconobbe il soggetto del ritratto!

In realtà Gabrio Piola è stato uno dei pionieri della fisica matematica in Italia. Ma che cosa si intende con questo termine? In passato, esso indicava quella branca della scienza che aveva permesso la soluzione di alcuni problemi specifici governati da equazioni alle derivate parziali, quali, ad esempio, la propagazione del calore, la teoria del potenziale, la teoria dell'elasticità; in questo senso Fourier, Lamé, Gauss, Beltrami, ecc., furono tra i più importanti fisici matematici. Oggi si riferisce allo sviluppo di metodi matematici rigorosi per l'applicazione a problemi in fisica. Il Journal of Mathematical Physics definisce il campo come "l'applicazione della matematica a problemi di fisica e lo sviluppo di metodi matematici adatti a tali applicazioni e alla formulazione di teorie fisiche". In realtà, nel periodo in cui operò Piola, l’epoca d’oro della meccanica celeste o terrestre, quasi tutti i matematici si confrontavano con problemi di fisica e la distinzione tra le varie discipline non era affatto stabilita rigorosamente.

Della giovinezza di Gabrio Piola non si hanno molte notizie se non che compì i primi studi in casa. Fu quindi iscritto a vari licei della città lombarda. Al liceo di S. Alessandro – oggi liceo Beccaria – studiò con il matematico e fisico barnabita Giuseppe Maria Racagni (1742-1822).

Compiuti gli studi liceali, si iscrisse all’università, che allora aveva sede a Pavia: dove incontrò un maestro di grande carisma, Vincenzo Brunacci (1768-1818), membro della Società Italiana delle Scienze e autore di un importante Corso di matematica sublime (cioè applicata alla fisica), pubblicato in quattro volumi fra il 1804 e il 1808. Brunacci era un convinto sostenitore di Joseph-Louis Lagrange, e pensava che il concetto di infinitesimo fosse da bandire dall’analisi e dalla meccanica. Piola ottenne il titolo di Dottore in matematica il 24 giugno 1816, ma la sua indole versatile non si limitava al solo studio delle scienze esatte, ma spaziava in più campi, come la filosofia, la teologia e la poesia.

Nei primi anni della Restaurazione, una brigata di giovani delle più ricche e nobili famiglie milanesi iniziò a incontrarsi nella Contrada del Chiossetto (vicino alla chiesa di San Pietro in Gessate) per darsi alla poesia. Dal luogo delle loro adunanze presero il nome di Accademia del Chiossetto o, con nome latineggiante, Accademia Clausetense. Negli anni successivi alla caduta di Napoleone infuriava la disputa tra Romantici e Classicisti; i salotti più progressisti di Milano sostenevano la necessità di rinnovare la poesia italiana, cercando ispirazione dalla poesia “barbarica”, come quella proveniente dall’Inghilterra e dalla Germania. Dall’altra parte vi era il partito dei Classicisti, che invece non voleva imitare ritmi, immagini e temi del mondo nordico; al contrario rivendicava la diversità della poesia italiana, che ha le sue radici in quella latina. Ovvia era la scelta di campo dell’Accademia, che ottenne anche la simpatia del voltagabbana Vincenzo Monti. L’Accademia del Chiossetto, anche se si riuniva per motivi esclusivamente poetici, aveva anche marcate coloriture politiche: essa radunava essenzialmente personalità moderate e reazionarie, molto legate agli ambienti clericali, che, pur non sostenendo l’ennesimo dominio straniero, preferivano di gran lunga la pace della Restaurazione alle guerre di Napoleone. Con il Congresso di Vienna tornava una politica più rispettosa delle differenze tra i ceti sociali e più aderente ai principi della fede cristiana. Piola fu del gruppo, cimentandosi, senza gran talento, con i versi, passione che non avrebbe mai abbandonato.

Nel 1818 moriva Vincenzo Brunacci e Piola ne redasse la commemorazione. Il sentimento di gratitudine dell’allievo verso il maestro trovò espressione anche nella riedizione degli Elementi di algebra e geometria del Brunacci. Questo manuale di successo, pensato per gli studenti dei licei e delle università, aveva già avuto tre edizioni. Piola ne curò la quarta nello stesso anno della scomparsa dell’autore, apportandovi diverse correzioni e riordinando la materia in alcuni punti, come ad esempio il capitolo dedicato alla trigonometria, che fu completamente riformulato. Nel 1824 sarebbe seguita una quinta edizione, con l’aggiunta di nuove note. Si trattava di opere che dimostrano la sensibilità di Piola per la divulgazione del sapere in una forma sempre più corretta e aggiornata: in questo solco si inseriva la pubblicazione delle Tavole logaritmiche in accompagnamento al già fortunato manuale. Intanto collaborava con il pavese Antonio Bordoni (1788-1860), allievo anch’egli del Brunacci e professore all’università di Pavia dal 1817, nell’allestimento delle Annotazioni agli Elementi di meccanica e d’idraulica dell’ingegnere e matematico bolognese Giuseppe Venturoli (1768-1846): le “annotazioni” rappresentarono un importante aggiornamento metodologico dell’opera, che aveva contribuito allo sviluppo degli studi sia della meccanica sia dell’idraulica in Italia; Piola e Bordoni rifecero, ricorrendo al metodo delle funzioni derivate di Lagrange, le dimostrazioni di Venturoli, che erano basate sull’uso degli infinitesimi.

Nel 1820 Piola fu nominato terzo allievo della Specola di Brera. La Specola Braidense era stata fondata nel 1764 dal gesuita dalmata Ruggero Boscovich. Nel 1773 la Compagnia di Gesù era stata soppressa nell’Impero austriaco e i suoi beni, incluso il palazzo di Brera, diventavano proprietà dello Stato. Da quel momento gli astronomi e gli allievi della Specola passarono alle dipendenze del Governo, che ne regolava anche la nomina. Nella Specola erano attivi tre astronomi (tra i quali Barnaba Oriani) e tre allievi. L’osservatorio, nonostante la stima di cui godeva a livello europeo, non aveva però una sufficiente dotazione economica: il governo austriaco trascurava la Specola e le promesse dell'imperatore Francesco I, in visita ufficiale nel 1825, non si tradussero mai in atti concreti. L’attività di studio e ricerca della Specola approdava nella pubblicazione delle Effemeridi astronomiche, che dal 1774 registravano le posizioni giornaliere del Sole e dei pianeti; nell’Appendice sì pubblicavano gli esiti delle ricerche degli astronomi stessi: fra queste c’è il primo contributo ufficiale di Piola in campo astronomico, Sulla teorica dei cannocchiali, del 1821. Tuttavia, non era l’astronomia il suo campo di interesse primario.

L’Imperial Regio Istituto Lombardo bandiva regolarmente dei concorsi a premi per lavori di ricerca scientifica. Un’apposita commissione individuava un tema da mettere a concorso. Gli elaborati pervenuti erano poi esaminati dai membri dell’Istituto: il vincitore riceveva un premio in denaro e il suo scritto veniva dato alle stampe. Il tema proposto nella seduta dell’Istituto del 4 ottobre 1822 era: “Si dimanda un’applicazione de’ principj contenuti nella Meccanica analitica dell’immortale Lagrange ai principali problemi meccanici e idraulici, dalla quale apparisca la mirabile utilità e speditezza dei metodi lagrangiani”. Si richiedeva dunque un’estensione della ricerca scientifica a partire da un testo fondamentale nel campo della fisica teorica del matematico italo-francese, il Traité de mécanique analytique, pubblicato in prima edizione a Parigi nel 1788.

Il problema fondamentale della meccanica ereditato dal secolo precedente consisteva nella determinazione del moto di punti materiali. In base alla concezione atomistica della materia, allora dominante, secondo la quale ogni corpo fisico è costituito da un numero finito di punti materiali, il moto di tutti i corpi doveva poter essere ridotto a loro sistemi; ma a tal fine era necessario, in primo luogo, comprendere il moto di un punto materiale. Il principio variazionale non si servì quindi, inizialmente, del metodo “diretto”, praticato con successo soprattutto da Newton, consistente nel ricondurre ogni variazione di moto (accelerazione) all'influsso di forze, bensì del metodo 'indiretto' del confronto: l'idea base del principio era di determinare, e quindi individuare univocamente, il moto effettivo del punto materiale tramite altri moti, soltanto pensati (virtuali) ma in linea di principio possibili, le cui particolari proprietà si potessero esprimere per mezzo di grandezze scalari.

Gli spostamenti virtuali sono slittamenti infinitamente piccoli del sistema, compatibili con i vincoli, ma al contrario di uno spostamento effettivo (anche di tipo infinitesimale), vanno contemplati come effettuati in un tempo nullo. Anche il lavoro necessario per essi è considerato “virtuale'” Questo principio richiede di ricondurre la dinamica alla statica, che si assume già sviluppata. Alla statica, cioè all'analisi di problemi di equilibrio, si riconduce anche la comparsa del principio dei lavori virtuali.

Il principio delle velocità virtuali assume importanza nella Mécanique analytique di Lagrange per il fatto di consentire un'organizzazione formale e deduttiva di ampie parti della meccanica. Egli introdusse a sua generalizzazione del principio delle velocità virtuali nella parte statica della sua opera come "une espèce d'axiome de Méchanique". Più tardi sostenne però che esso non possedeva l'evidenza tradizionalmente necessaria a un assioma. Egli cercò quindi di dimostrarlo per diverse vie, ma queste dimostrazioni sono considerate oggi piuttosto come petizioni di principio che non come derivazioni logiche da basi sicure.

Come è evidente dal tema proposto, la meccanica lagrangiana era considerata il metodo fondamentale per una nuova formulazione della meccanica proposta da Newton. Non è infatti agevole servirsi dell’’equazione di Newton quando la si debba riscrivere facendo uso di coordinate diverse da quelle cartesiane. La questione diventa ancor più difficile quando si considerino non solo punti materiali liberi di vagare per lo spazio, ma corpi estesi, o sistemi di punti tra loro connessi mediante vincoli di vario tipo. Il formalismo lagrangiano risolve in modo elegante il problema di scrivere le equazioni della dinamica, almeno quando siano soddisfatte alcune ipotesi in qualche senso naturali. Si trattava di un metodo in cui le equazioni del moto sono descritte tramite delle equazioni variazionali di Eulero (equazioni differenziali del secondo ordine), dove la funzione scalare argomento è la lagrangiana di Newton L, cioè la differenza tra energia cinetica T e potenziale V:

,

in cui si intende che sia l’energia cinetica T che l’energia potenziale V debbano essere espresse in funzione delle coordinate lagrangiane

 

delle velocità generalizzate

e del tempo t.

Nel descrivere sistemi in cui l'energia si conserva, la lagrangiana dipende soltanto dalle coordinate q e dalle loro derivate , in quanto il potenziale non dipende dal tempo. La dinamica di un sistema di N punti materiali soggetto a vincoli e a forze attive dipendenti dal potenziale è retta dalle equazioni di Lagrange:

dove L indica la lagrangiana di Newton. É questa la forma delle equazioni di Lagrange usata più di frequente. In questo modo, non è necessario utilizzare campi vettoriali. Il vantaggio più immediato consiste nel fatto che nel caso di sistemi vincolati è possibile ottenere le equazioni del moto senza dover tener conto delle reazioni vincolari, che sono per lo più indeterminate. A questo fine è sufficiente sostituire nella Lagrangiana per il sistema non vincolato una opportuna parametrizzazione del vincolo.

La ricerca di Piola Sull’applicazione de’ principj della Meccanica analitica del Lagrange ai principali problemi venne considerata la più meritevole fra quelle presentate e nell’adunanza solenne del 4 ottobre 1824 fu premiata con un riconoscimento monetario di 1500 lire italiane e con la pubblicazione. Nel stesso anno aveva ricevuto l’offerta della cattedra di matematica applicata presso l’Università di Pavia: era una proposta prestigiosa che il matematico tuttavia non accettò.

All’inizio della sua Memoria, Piola metteva in evidenza gli argomenti tralasciati da Lagrange che egli intendeva trattare: la descrizione del moto dei sistemi continui lineari, dei sistemi continui superficiali, l’analisi di alcuni problemi di idraulica e il riordinamento delle formule lagrangiane sul moto di rotazione. Egli partì da un principio fondamentale, ponendosi in contrasto con Lagrange: concentrare l’attenzione sul movimento, tralasciando il problema degli equilibri. Sul piano logico, a parere di Piola, occorreva premettere lo studio della dinamica e, a partire da quella, derivare il problema della statica.

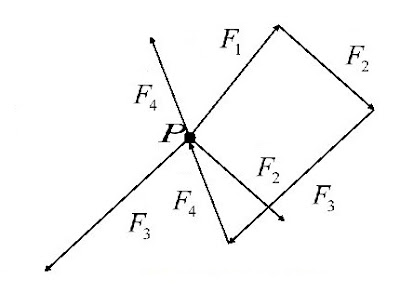
Per lo studio del moto del punto materiale Piola riteneva che l’unico principio necessario fosse quello di sovrapposizione dei moti (spostamenti). Il principio è di carattere empirico; ciò non di meno esso appare assolutamente evidente perché́ fa riferimento all’esperienza di tutti i giorni; lo stesso non si può̀ dire del principio delle velocità virtuali: «Lagrange stesso ne convenne quando disse: quant à la nature du principe des vitesses virtuelles il faut convenir qu’il n’est pas assez évident». Secondo il principio di sovrapposizione dei moti (spostamenti), se si hanno due moti dovuti a due «cause» diverse, il moto risultante è pari alla somma vettoriale dei due moti. Un punto materiale è in equilibrio se e solo se i moti componenti si annullano tra loro. Con il principio della composizione dei moti si risolve non solo il problema del moto ma anche quello dell’equilibrio.

In secondo luogo, Piola criticava il ricorso ai concetti di velocità e di forza, “enti oscuri e metafisici dai quali bisogna distogliere il pensiero se si vuole avere chiarezza di concetti nello stabilire le equazioni relative al moto; le sole idee di spazio e di tempo sono invece concetti chiari e utili allo scopo”. Il metodo lagrangiano delle funzioni analitiche poteva essere applicato alla soluzione dei problemi di meccanica e Lagrange stesso lo aveva fatto parzialmente, ma non in maniera esauriente. Lagrange, partendo dal principio delle “velocità virtuali”, aveva dedotto le leggi dell’equilibrio e del moto espresse per mezzo di equazioni analitiche. Piola criticava proprio il fatto che il principio di base non era frutto di una dimostrazione bensì era stato posto come assioma. Proponeva, quindi, di sgomberare il campo dal concetto di “infinitamente piccolo” introdotto da Lagrange, che supponeva l’esistenza di un “moto minimo” nell’esposizione del principio delle “velocità virtuali”, che non era ricavato dall’esperienza.

Lo scritto voluminoso di Piola andava ben oltre il tema proposto dall'Istituto Lombardo, cosa che era stata notata e lodata anche dai commissari giudicanti. Barnaba Oriani e Francesco Carlini, estensori del giudizio di merito, rilevarono la diversità dell’approccio applicato da Piola rispetto a Lagrange: “(...) mostrando una decisa ripugnanza a quelle velocità virtuali e ancora ad ogni idea di infinitesimi, ricorre a un nuovo metodo che ha qualche rassomiglianza con quello usato due secoli prima dall’insigne matematico Bonaventura Cavalieri nella sua Geometria degl’indivisibili e che propriamente chiamasi metodo dei limiti”. Il milanese Cavalieri fu un riferimento costante per Piola, che avrebbe poi scritto una lunga e dettagliata commemorazione in occasione dell’inaugurazione della statua dedicatagli nel cortile di Brera.

Le concezioni epistemologiche di Piola sulla scienza in generale e sulla matematica in particolare sono contenute nelle Lettere di Evasio ad Uranio intorno alle scienze matematiche (Modena 1825), nel quale le verità della fede vengono confrontate con quelle della scienza, evidenziando un possibile accordo, a patto che non si metta in discussione il primato divino. Tra il fare scienza e la pratica della fede non vi è contrasto: ammettere l’esistenza di un ente eterno e creatore non è un ostacolo alla conoscenza scientifica del mondo; conoscere scientificamente il mondo, d’altro lato, può essere anzi un (ulteriore) invito alla fede.

“Raccogliendo il discorso, conchiuderemo essere buona cosa lo studiare le scienze, migliore il saper conservare la prima e la più importante di esse, che ci fu insegnata da un Maestro divino: essere conveniente il consultare le opere dei dotti scrittori, ma insieme di essenziale prudenza, specialmente a’ dì nostri, il non consolidarsi mai con alcuno in una università̀ di opinioni. Infatti, quegli stessi, che ci vorrebbero insidiare la religione, non sono essi i primi a millantare un dominio sui propri giudizi, una libertà di pensare, una costanza negli assunti principii? Ora mantiene in verità̀ il diritto di giudicare chi non si arrende a vieti sofismi, meno poi a certi frizzi maligni, che non vestono larva di ragionamento; fa l’uso più perfetto di sua libertà chi umilia la ragione davanti alla Fede con un ossequio, che dalla ragione stessa esaminato viene riconosciuto doveroso; è veracemente d’animo forte, e di carattere fermo chi per qualunque urto non si smuove dai fondamenti della sua religiosa credenza”.

Nonostante la rinuncia alla carriera accademica, Piola dedicò molto del suo tempo alla didattica della matematica e tenne regolari lezioni presso la sua casa, coadiuvato dal matematico e astronomo Paolo Frisiani. Tra i suoi allievi vi furono Francesco Brioschi, più tardi professore di meccanica razionale a Pavia e fondatore del Politecnico di Milano, e Placido Tardy, poi professore di matematica all’Università di Messina. Nel suo cosiddetto “Centro di matematica” Piola commentava gli autori più significativi e, fatto più importante, discuteva e divulgava le teorie che non trovavano ancora spazio nelle lezioni accademiche.

Tra gli autori più studiati a casa Piola c’era Augustin Louis Cauchy, il grande matematico francese ultrabigotto e reazionario (Abel lo aveva definito un cattolico pazzo). che, a seguito dei moti del luglio del 1830 contro il potere assoluto dell’ultimo re borbonico Carlo X e al colpo di stato di Filippo d’Orleans, aveva deciso di lasciare la Francia e aveva insegnato a Torino fra il 1831 e il 1833 su invito del re piemontese Carlo Alberto (quando andava a Milano era ospite in casa Manzoni). Con lui Piola era in corrispondenza almeno dal 1826.

Cauchy si era fatto precedere dalla pubblicazione di un lungo articolo in italiano intitolato Sui metodi analitici, pubblicato nell’inverno 1830-31 dalla Biblioteca Italiana di Milano. In questo lavoro presentava un’introduzione ai metodi dei suoi corsi all’École Polytechnique di Parigi. Nella prefazione, volle dimostrare che cosa significasse il suo “bisogno di rigore”. Criticando apertamente l’indeterminatezza dei metodi lagrangiani di calcolo, spiegava come il suo rigore si rifletteva su concetti fondamentali come quelli di derivata, integrale, integrazione delle equazioni differenziali. Ma il tono era pedante e generò una reazione ostile tra molti matematici italiani, ancora legati all’approccio lagrangiano al Calculus. Solo Gabrio Piola, anche perché di sentimenti politici e religiosi affini al francese, prese subito posizione a favore di Cauchy, diventandone poi il profeta in Italia (e i reazionari in politica furono tra i più innovativi in campo matematico). Lo stesso Piola avrebbe poi tradotto l’opuscolo scritto da Cauchy in difesa della religione cattolica contro “l’abuso dell’ingegno e della scienza adoperati a corrompere i cuori e pervertire le menti”, nel quale si criticava apertamente il materialista Laplace.

Piola fu eletto tra i dotti del Regio Istituto lombardo nel 1828 (per diventarne membro effettivo nel 1839), divenne membro della Società italiana delle scienze (Accademia dei XL), socio corrispondente della Nuova Accademia pontificia dei Lincei. Partecipò ai Congressi degli scienziati italiani che cominciarono a tenersi con cadenza annuale dal 1839. Fu anche editore di una rivista, Opuscoli matematici e fisici di diversi autori (Milano 1832-34), di cui uscirono solo due volumi. Tra l’altro, tale rivista fu il mezzo di diffusione delle teorie matematiche di Cauchy in Italia, contenendo alcuni dei suoi lavori fondamentali tradotti in italiano da Piola e Frisiani (Sulla meccanica celeste e sopra un nuovo calcolo chiamato calcolo dei limiti, Sui principj e sugli usi del calcolo dei residui). Una curiosità: la prima delle due memorie era stata presentata all’Accademia delle Scienze di Torino nell’ottobre 1831 per criticare la scuola lagrangiana di Giovanni Piana.

Anche nei lavori successivi Piola fu sempre guidato dall’ambizione di migliorare la teoria meccanica di Lagrange su due fronti: sul versante matematico occorreva eliminare il concetto degli infinitesimi; sul versante fisico era necessario fare chiarezza su alcuni principi enunciati da Lagrange stesso.

I suoi contributi più importanti si trovano sparsi nei lavori di matematica-fisica. I prodotti fondamentali in questo settore sono quelli di meccanica del continuo, che si occupa delle proprietà fisiche di solidi e fluidi che sono indipendenti da qualsiasi particolare sistema di coordinate in cui sono osservati. Queste proprietà fisiche sono rappresentate da tensori, che sono oggetti matematici che hanno la proprietà di essere indipendenti dal sistema di coordinate. Questi tensori possono essere espressi in sistemi di coordinate per comodità di calcolo.

I materiali, come solidi, liquidi e gas, sono composti da molecole separate dallo spazio. Su scala microscopica, i materiali mostrano separazioni e discontinuità. Tuttavia, alcuni fenomeni fisici possono essere modellati assumendo che i materiali esistano come un continuo, il che significa che la materia nel corpo è continuamente distribuita e riempie l'intera regione dello spazio che occupa. Un continuo è un corpo che può essere continuamente scomposto in elementi infinitesimali con proprietà che sono quelle dell'intero volume del materiale.

Modellare un oggetto come un continuo presuppone che la sostanza dell'oggetto riempia completamente lo spazio che occupa. Modellare gli oggetti in questo modo ignora il fatto che la materia è fatta di atomi, e quindi non è continua; tuttavia, su scale di lunghezza molto maggiori di quelle delle distanze interatomiche, tali modelli sono molto accurati. Leggi fisiche fondamentali come la conservazione della massa, la conservazione della quantità di moto e la conservazione dell'energia possono essere applicate a tali modelli per derivare equazioni differenziali che descrivono il loro comportamento; alcune informazioni sul materiale in esame vengono aggiunte attraverso relazioni costitutive.

Alla base delle opere di Piola c’è una posizione di fondo già evidente nella memoria giovanile del 1825, la stessa che si trova in Lagrange: tutta la meccanica può essere espressa per mezzo del calcolo differenziale, dichiarando di voler fondare la sua meccanica solo sui concetti base di tempo e di spazio (geometria); rinunciando al concetto di forza, che non è necessario, anche se può essere utile in quanto «vestendo d’immagini molte proprietà del moto se le rendono più famigliari»

Di sicuro uno dei contributi più rilevanti di Piola alla meccanica del continuo è il modo in cui introduce le componenti delle forze interne. Queste non sono concepite come forze scambiate tra molecole o particelle ultime componenti la materia, ma piuttosto come moltiplicatori indeterminati di Lagrange di opportune equazioni di vincolo.

Nel saggio del 1833 La meccanica dei corpi naturalmente estesi trattata con il calcolo delle variazioni, Piola andava oltre, estendendo l’applicazione dei principi della meccanica razionale ai corpi rigidi. Lagrange aveva elaborato sei equazioni di equilibrio dei corpi – le sei equazioni cardinali della statica – ma la sua attenzione si era però fermata sul problema dell’equilibrio globale, non dell’equilibrio locale. Piola. già nella Memoria del 1824 aveva spiegato che esistono nei corpi delle forze interne delle quali non è possibile farci un’idea chiara intorno alla maniera in cui interagiscono: perché un corpo sia in equilibrio, anche queste forze interne devono esserlo.

Lo studio dei sistemi di punti materiali che interagiscono tra loro richiede l’introduzione di altri principi e concetti; in particolare si devono introdurre le masse. Piola si rendeva conto della difficoltà, insita alla teoria dinamica da lui scelta. Risolse il problema ammettendo l’esistenza di “atomi” di materia tutti uguali tra loro. La massa di un aggregato è proporzionale al numero di atomi. Oltre al concetto di massa dovette introdurre anche il principio di azione e reazione. Secondo Piola tale principio, che non era mai nominato come tale, poteva essere riguardato in parte come principio di ragione, in parte come principio empirico.

Lo scopo di sviluppare una teoria meccanica rigorosa da un punto di vista matematico formale avveniva così con la rinuncia, almeno parziale, del rigore dal punto di vista fisico. Infatti, i principi assunti, la sovrapponibilità̀ dei moti e il principio dei lavori virtuali non erano giustificati in modo convincente. Ciò̀ nonostante, i risultati raggiunti da Piola furono fondamentali, dimostrando l’importanza fondamentale della meccanica analitica.

Piola iniziava il suo saggio del 1833 affermando che benché la Mécanique analytique fosse considerata la massima opera di meccanica e le sue tecniche rappresentassero la “vera meccanica filosofica”, di fatto essa doveva essere aggiornata e integrata. Piola si poneva così il problema di estendere le tecniche della Mécanique in modo che esse potessero essere applicate utilmente anche per i corpi estesi.

Attraverso lunghi calcoli, arrivava a elaborare le equazioni di condizione che esprimono l’equilibrio delle forze interne (1 e 2, cioè la rigidità dei corpi), riuscendo poi a dimostrare l’equivalenza tra tali formule con le equazioni indefinite di equilibrio (3 e 4). Tale dimostrazione nella letteratura internazionale va sotto il nome di teorema di Piola. 

 

Piola non era sempre cosciente della rilevanza dei suoi sviluppi, come accade sempre per quasi tutti i precursori, e non si accorse di avere introdotto una grandezza che sarebbe diventata importante. Si tratta del tensore nominale di tensione (o tensore di stress) P di Piola-Kirchhoff, indispensabile per lo studio del problema statico dei continui soggetti a grandi spostamenti, perché descrive le sollecitazioni e le deformazioni sia nella configurazione di riferimento che in quella corrente.

Piola scrisse anche importanti memorie di matematica pura sulle differenze finite e sulla teoria dell’integrazione, soprattutto in Note relative al calcolo degli integrali definiti (1846) e in Sull’applicazione del calcolo delle differenze finite alle questioni di analisi indeterminata (1850). Eugenio Beltrami riprenderà una generazione dopo l’approccio di Piola.

Sebbene sia stato uno dei più brillanti meccanici razionali del XIX secolo, probabilmente il più brillante degli italiani, Gabrio Piola è autore poco conosciuto e valutato. Ciò è dovuto a varie ragioni: di carattere generale, associate al provincialismo scientifico dell’Italia del tempo, e di carattere particolare, come la sua scelta di scrivere soltanto in italiano, nonostante conoscesse a fondo gli sviluppi francesi della matematica fisica. Nonostante i suoi concittadini lo conoscessero ben poco, il suo nome è tuttavia uno dei pochi a essere ancora citato nella letteratura moderna della meccanica del continuo.

Morì nella sua villa di Giussano, in Brianza, il 9 novembre 1850.

Levi-Civita e il trasporto parallelo

A Padova

Tullio Levi-Civita (1873-1941) si era formato all'Università di Padova con il geometra Giuseppe Veronese e Gregorio Ricci Curbastro. Quest'ultimo, che aveva sviluppato il calcolo tensoriale tra il 1885 e il 1895, diresse la sua tesi di laurea, discussa nel 1892. Unendo il metodo di Ricci-Curbastro con alcuni risultati della teoria dei gruppi di trasformazione di Lie, Levi-Civita estese la teoria degli invarianti assoluti a casi più generali di quelli considerati dal suo maestro e risolse un problema classico della meccanica analitica, trasformando un sistema di equazioni della dinamica, in caso di assenza di forze esterne, in un sistema più semplice, avente le stesse traiettorie rappresentate dalle geodetiche in una varietà riemanniana a n-dimensioni. L'uso del calcolo tensoriale era essenziale per la soluzione di questo problema. 

Levi-Civita fu nominato professore di meccanica razionale a Padova nel 1897 e continuò a lavorare con Ricci Curbastro. Nel 1901 pubblicarono insieme nei Mathematische Annalen l’articolo Méthodes de Calcul Differentiel Absolu et leurs Application, scritto su invito di Felix Klein, che diventò subito il manifesto del calcolo tensoriale. Nella memoria, Ricci Curbastro e Levi-Civita illustravano gli elementi fondamentali di questo metodo, che chiamarono "un nuovo algoritmo", grazie al quale erano in grado di esprimere diverse relazioni di geometria ma anche dell'analisi e della fisica matematica (come equazioni di elasticità o di elettromagnetismo) indipendentemente dal sistema di coordinate scelto. La loro teoria mostrò la sua efficacia soprattutto negli spazi con n dimensioni (varietà riemanniane), che Levi-Civita aveva già studiato nella sua tesi. 

La corrispondenza con Einstein 

Il calcolo tensoriale ebbe un ruolo essenziale nella formulazione della teoria della relatività generale elaborata da Albert Einstein. Nel 1923, ricordando il momento in cui si rese conto che il calcolo tensoriale poteva essere il linguaggio appropriato per esprimere la relatività generale, Einstein scriveva: 

"Tuttavia, ho avuto l'idea decisiva dell'analogia tra il problema matematico della teoria [della relatività generale] e la teoria gaussiana delle superfici solo nel 1912, dopo il mio ritorno a Zurigo, quando ancora non conoscevo le opere di Riemann, Ricci e Levi-Civita. Questi [lavori] sono stati portati alla mia attenzione per la prima volta dal mio buon amico Grossmann.” 

Marcel Grossmann era professore di matematica all'Università di Zurigo e amico di Einstein sin da quando erano studenti. Sebbene avesse indicato questi testi nel 1912, Einstein impiegò tre anni per apprendere le tecniche della geometria differenziale e del calcolo tensoriale che gli consentirono di superare le difficoltà matematiche del suo lavoro. Così diceva a un corrispondente: 

“Sto lavorando esclusivamente al problema della gravitazione, e credo di poter superare tutte le difficoltà con l’aiuto di un mio amico matematico di qui [Grossmann]. Ma una cosa è certa: non ho mai faticato tanto in vita mia, e ho acquistato un enorme rispetto per la matematica, le cui parti più sottili consideravo finora, nella mia ignoranza, come un puro lusso. Al confronto di questo problema, l’originaria teoria della relatività è un gioco da ragazzi”. 

Nel 1913 apparve il primo risultato della sua collaborazione con Grossmann: l’articolo Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation [Lineamenti di una Teoria della Relatività generalizzata e di una Teoria della Gravitazione], ma il problema cruciale delle equazioni di campo gravitazionale era irrisolto: nell’articolo le equazioni di campo non sono considerate generalmente covarianti, ma il loro gruppo invariante è limitato alle sole trasformazioni lineari. Questo punto di vista portò Einstein e Grossmann a fare supposizioni fisiche errate. In alcuni documenti successivi, Einstein e Grossmann tentarono di giustificare le equazioni di campo gravitazionale derivate nell’Entwurf per mezzo di principi variazionali. 

Le difficoltà connesse con la giusta espressione delle equazioni gravitazionali furono il soggetto principale della corrispondenza tra Einstein e Levi-Civita. Einstein fu sempre grato a Levi-Civita per il suo interesse per la relatività generale. Nelle lettere, Levi-Civita notò un errore nella dimostrazione presente nell’articolo, le cui conseguenze coinvolgono le proprietà covarianti del tensore gravitazionale. Einstein tentò più volte di confutare le obiezioni di Levi-Civita. In una lettera datata 5 marzo 1915, scrisse: 

“Caro collega, sono molto felice che lei sia così interessato al mio lavoro. Può immaginare quanto raro sia qualcuno che sia profondamente interessato a questo argomento con una mente indipendente e senza pregiudizi. [...] Quando ho notato che ha criticato la prova più importante della mia teoria, ottenuta con fiumi di sudore, ero non poco preoccupato dal fatto che so che sa gestire tali questioni matematiche molto meglio di me. Tuttavia, dopo un'attenta riflessione, penso che la mia dimostrazione può essere accolta”. 

Lo stesso Einstein scrisse a Levi-Civita, in italiano, il 2 aprile 1915: 

“Una corrispondenza così interessante non mi era ancora capitata. Dovrebbe vedere con quale ansia aspetto sempre le sue lettere.” 

Il 21 aprile 1915 Einstein scrisse a Levi-Civita che sperava di persuaderlo della validità del "suo Teorema", poiché - secondo lui - l'obiezione del suo corrispondente italiano poteva essere superata. La discussione epistolare tra Einstein e Levi-Civita andò avanti fino all'inizio di maggio. Il 5 maggio 1915, Einstein dovette ammettere che la sua dimostrazione era "difettosa". 

In una serie di quattro articoli presentati all'Accademia delle Scienze prussiana nel novembre 1915, Einstein pubblicò la versione finale delle equazioni del campo gravitazionale, ora chiamate equazioni di Einstein. L’articolo definitivo fu il quarto, Feldgleichungen der Gravitation [Le equazioni del campo gravitazionale]. 

Il trasporto parallelo 

Levi-Civita pubblicò l’articolo sul trasporto parallelo Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura riemanniana nel 1917, in Rendiconti del Circolo Matematico di Palermo, che in quel periodo godeva di una grande reputazione internazionale e pubblicava articoli di matematica di altissimo livello.

La memoria di Levi-Civita, subito dopo la Grande Guerra, ebbe molto successo: numerosi articoli sul trasporto parallelo furono tempestivamente pubblicati, molti colleghi lodarono l'efficacia di questo nuovo metodo e gli studenti venivano a Roma per lavorare con Levi-Civita su questioni relative a questo nuovo metodo. Le lezioni presso l'Università di Roma sul calcolo tensoriale, pubblicate nel 1925 dalla casa editrice Stock in un volume tradotto in inglese e tedesco nel 1927 e nel 1928, poi usato dai matematici di tutto il mondo come strumento sia di ricerca sia d’insegnamento, diedero ulteriore impulso al concetto di trasporto parallelo. 

Che cos’è il trasporto parallelo? Nella geometria piana di Euclide, il parallelismo gioca un ruolo chiave. Per Euclide, due linee sono parallele se, infinitamente prolungate, non si incrociano mai. Una formulazione moderna del quinto postulato di Euclide afferma che, per un punto al di fuori di una data retta, passa solo una retta parallela ad essa. Cambiare questo postulato porta all'invalidazione di diversi teoremi della geometria euclidea ed è quindi il primo passo per sviluppare le geometrie non euclidee. Fu Levi-Civita a introdurre il concetto di parallelismo su uno spazio multidimensionale (varietà riemanniana) nel suo articolo del 1917. Il suo obiettivo non era quindi quello di elaborare una teoria geometrica, ma piuttosto di "semplificare" i simboli di Riemann che esprimono la curvatura di una varietà dando loro anche un'interpretazione geometrica. Infatti, come Levi-Civita dichiarò all'inizio del suo articolo, 

"La teoria della gravitazione di Einstein [...] considera la struttura geometrica dello spazio ambiente correlata, molto debolmente ma intimamente, ai fenomeni fisici che vi si verificano (sic); ciò differisce dalle teorie classiche [come la meccanica newtoniana], che considerano lo spazio fisico come un dato a priori. Lo sviluppo matematico della concezione grandiosa di Einstein (che trova il suo naturale strumento algoritmico nel calcolo differenziale assoluto di Ricci) fa della curvatura di una certa varietà quadridimensionale e dei simboli relativi di Riemann un elemento essenziale". 

Con curvatura si indica una serie di concetti geometrici che intuitivamente si riferiscono alla misura di quanto un determinato oggetto si discosti dall'essere piatto. La misura della curvatura viene definita in modi diversi a seconda dell'ente geometrico cui è applicata. Ad esempio, una linea nel piano o un piano nello spazio tridimensionale hanno curvatura nulla. Un cerchio nel piano ha una curvatura costante, tanto più grande quanto più piccolo è il raggio. Si distinguono due tipi essenziali di curvatura: 

• curvatura estrinseca: è la curvatura posseduta dall'oggetto in relazione ad uno spazio piatto di dimensione superiore in cui è immerso, determinabile solo confrontando elementi dell'oggetto in relazione ad elementi dello spazio contenitore; 

• curvatura intrinseca (o gaussiana): è la curvatura determinabile utilizzando solo operazioni eseguite su elementi dell'oggetto medesimo. 

Per quanto riguarda la definizione di parallelismo in questi spazi, consideriamo tale definizione nel caso più semplice di superfici curve. Levi-Civita nelle lezioni del 1925 adottò l'approccio pedagogico che consiste di definire prima il parallelismo per le superfici e poi generalizzarlo alle varietà. Inizialmente, egli osservava che nel piano euclideo, se consideriamo due punti P e P₁ per ogni "direzione", da P si può costruire una e una sola direzione che passa per P₁ e parallela alla direzione data; per lui, una "direzione" u è definita attraverso il "vettore unitario" che gli corrisponde. Questa costruzione, osserva Levi-Civita, può essere facilmente generalizzata alle cosiddette superfici sviluppabili. Una superficie Σ è "sviluppabile" se, immaginandola "flessibile e inestensibile", può essere sovrapposta a una regione del piano "senza strappi e senza duplicazione". Essa viene detta anche rigata, intendendo che è possibile costruire una famiglia infinita di rette interamente contenute in essa. Gli esempi più semplici di superfici sviluppabili sono i cilindri e i coni senza il vertice.

Se Σ è sviluppabile, Levi-Civita introduce un'applicazione - denominata "parallelismo di superficie" - tra le direzioni in P tangenti a Σ e le analoghe direzioni che escono da P₁, un altro punto di Σ, in modo che a ogni direzione u corrisponde la direzione u₁ che diventa parallela a u nel senso abituale quando si sovrappone Σ sul piano; le direzioni u e u₁ sono allora dette "parallele nel senso della superficie".

Ovviamente tale criterio non sarà più valido se Σ non è una superficie sviluppabile, anche se si tratta di una superficie elementare, come per esempio la superficie sferica. In questo caso bisognerà considerare il punto P₁ come proveniente da P seguendo una certa curva T, denominata "curva di trasporto." Questa è una visione cinematica che permette a Levi-Civita di definire il trasporto parallelo da P a P₁ utilizzando la sviluppabile circoscritta a Σ lungo la curva T; questa superficie, che egli indica con Σ_T, sarà perciò tangente a Σ lungo T e, in particolare, in P e P₁. Levi-Civita chiama "la parallela da P₁ a una direzione qualunque (superficiale) u attraverso P lungo la curva T, la direzione (superficiale) u₁ che sulla sviluppabile Σ_T è parallela a u nel senso appena definito." Ad esempio, nel caso di una sfera, se T è la linea equatoriale, allora la sua superficie sviluppabile Σ_T sarà un cilindro; se T è un parallelo non equatoriale, Σ_T sarà un cono. In generale, la superficie della sfera non è isometrica al piano, neanche localmente: in altre parole, nessun dominio della sfera, per quanto piccolo sia, può essere applicato su un dominio del piano in modo da conservare le distanze.

In generale, questa definizione di parallelismo dipende dalla curva di trasporto. Levi-Civita non manca di sottolineare che la nozione geometrica di parallelismo è "vicina" a quella di lavoro in fisica. In effetti, il lavoro svolto per trasportare, ad esempio, un corpo materiale da A a B dipende dalla curva scelta per andare da un punto all'altro. Consideriamo alcuni esempi. Innanzitutto, sul piano euclideo, tutti i vettori torneranno esattamente a se stessi dopo il trasporto parallelo su qualsiasi curva chiusa. Nella figura, se portiamo il vettore parallelo da P lungo il circuito dato, esso coinciderà con il vettore iniziale dopo un giro completo, poiché nel piano troviamo la nozione abituale di parallelismo. Si potrebbe fare la stessa osservazione per tutte le superfici sviluppabili.

E su una superficie non sviluppabile? Consideriamo il caso della superficie sferica: da A il vettore della figura viene trasportato parallelamente lungo le curve AN, NB, BA che sono linee geodetiche. Per portare il nostro vettore in parallelo usiamo la definizione di Levi-Civita che impiega le superfici sviluppabili lungo una curva: in questo caso, ogni tratto di geodetica (cerchio massimo) si sviluppa su un cilindro. Tuttavia, alla fine del suo circuito, ritornando ad A, il vettore crea un certo angolo α con la sua direzione iniziale che era tangente alla curva. Invece, se il trasporto parallelo è fatto lungo un meridiano della sfera, ad esempio il circolo massimo ANSA, tornando ad A il vettore sarà ancora tangente alla curva: coinciderà con il vettore iniziale.

Pertanto, anche su una superficie di curvatura costante come la sfera, il trasporto parallelo non può essere pensato indipendentemente dalla curva scelta per trasportare il vettore. Il trasporto parallelo su tale tipologia di superfici non sviluppabili è si può effettuare mediante lo stesso processo geometrico-cinematico previsto per una superficie sviluppabile, con la sola condizione che la curva di trasporto T sia una porzione compresa tra P e P₁ di una geodetica. Nel caso particolare di una sfera, le geodetiche sono tutti i paralleli e tutti i meridiani (usando una terminologia tipicamente geografica).

Una notevole proprietà del parallelismo, che è una conseguenza immediata della sua definizione, riguarda la conservazione degli angoli: infatti, Levi-Civita constata che, se a e b sono due direzioni per P, alle quali corrispondono le direzioni parallele a₁ e b₁ che passano per P₁. allora formano lo stesso angolo. Questa proprietà non dipende dalla superficie (o dalla varietà) o dalla curva di trasporto. Un'altra conseguenza interessante della nozione di parallelismo si verifica quando la curva di trasporto è una geodetica. Come nel piano euclideo, in cui le geodetiche sono linee rette, possiamo considerare su una superficie una geodetica e una direzione che si muove in modo tale che il suo punto di applicazione appartenga sempre alla geodetica. Diremo che la direzione si muove "parallela" se forma sempre lo stesso angolo con la tangente alla geodetica. In particolare, la tangente a una geodetica sarà parallela a se stessa se si muove lungo la geodetica. In conclusione, scrive Levi-Civita, "le geodetiche sono curve auto-parallele". Inoltre, "da queste considerazioni deduciamo che l'auto-parallelismo è una proprietà caratteristica delle geodetiche e può essere usato per definirle". Ad esempio, se consideriamo i due percorsi 1 e 2 su una superficie sferica, la linea 1 è una geodetica perché la sua tangente si muove parallela a se stessa, mentre la linea 2 non è una geodetica perché, se si trasporta parallelamente il vettore inizialmente tangente alla curva, si ottengono vettori che in generale non saranno più tangenti alla curva. Si può quindi dire che nel trasporto parallelo di un vettore in un sistema generico di coordinate le sue componenti cambiano, a differenza di ciò che accade in metrica piatta: per trasporto parallelo si intende infatti il trasporto del vettore effettuato mantenendo costante l'angolo che esso forma con la superficie curva. 

Nel suo corso, Levi-Civita introduce l'apparato formale necessario per fare i calcoli in caso di parallelismo di superfici, e poi generalizza queste nozioni al caso delle varietà, arrivando a risolvere il problema iniziale dichiarato all'inizio del suo articolo del 1917: quello di dare alla curvatura della varietà un significato geometrico. Infatti, considerando su una varietà un circuito "infinitesimale" (formato da quattro archi di geodetica paralleli a due a due) e facendo muovere "per parallelismo" un vettore lungo questo circuito, trova una relazione che esprime il legame profondo tra il tensore di curvatura e il trasporto parallelo. 

Infine, si può osservare come l'introduzione di un nuovo e importante concetto di geometria differenziale, la deviazione geodetica, sia stata di nuovo ispirata dalla fisica. Nell’articolo pubblicato nel 1927, Levi-Civita analizza due punti infinitamente vicini appartenenti a due geodetiche diverse in una varietà riemanniana e ne studia la distanza. Fisicamente, le linee geodetiche possono essere interpretate come le traiettorie di due particelle di prova in caduta libera che sono infinitamente vicine l'una all'altra e che inizialmente si muovono parallelamente. È la curvatura dello spazio, che è responsabile di una deviazione tra le due particelle, che Levi-Civita chiama "deviazione geodetica" (e il pensiero corre per istinto verso il clinamen di Lucrezio). In generale, la fisica è una costante fonte di ispirazione per Levi-Civita. Inoltre, ai suoi occhi non ci sono veri e propri confini tra la fisica e la geometria differenziale: queste due discipline sono le facce di una stessa medaglia unificate da un linguaggio comune che è il calcolo tensoriale. 

Il trasporto parallelo consentì allo stesso tempo lo sviluppo delle teorie fisiche e della geometria differenziale in modo significativo. Le lezioni universitarie semplici e pedagogiche di Levi-Civita furono uno strumento straordinario per diffondere le sue idee sul calcolo tensoriale e in particolare sul parallelismo. Il trasporto parallelo, che stabilisce il legame tra geometria e fisica, occupa un posto centrale in questi testi. 

A Roma 

Nel 1918, Levi-Civita diventò professore all'Università di Roma, dove ebbe l'opportunità di partecipare alla fondazione di una vera scuola matematica internazionale. Vito Volterra, Federico Enriques, Guido Castelnuovo e Francesco Severi furono alcuni dei matematici che animarono questa scuola. Nel corso degli anni ‘20, Levi-Civita fu il referente italiano dell’Educational Board della Fondazione Rockefeller, un'organizzazione internazionale che aiutava i giovani scienziati nel periodo tra le due guerre mondiali. Con questa posizione istituzionale, Levi-Civita e i suoi colleghi accolsero all'Università di Roma diversi borsisti, che lavoravano in varie discipline matematiche come la geometria algebrica, l’analisi funzionale, il calcolo tensoriale, l’idrodinamica e la geometria differenziale. Durante gli anni '20 e '30, molte opere ispirate alle idee di Levi-Civita apparvero sulle riviste di settore. Scritti di suoi studenti o collaboratori furono spesso comunicati da lui stesso all'Accademia dei Lincei e pubblicati nei Rendiconti. 

Lo scopo di molti libri sul calcolo tensoriale pubblicati dopo la formulazione della relatività generale era quello di aiutare i fisici a capire il formalismo usato da Einstein per dedurre le sue equazioni del campo gravitazionale. Al contrario, le lezioni di Levi-Civita erano rivolte ai matematici e mostravano il calcolo tensoriale da un diverso punto di vista, dove la geometria giocava il ruolo più importante. L'approccio di Levi-Civita poté essere apprezzato anche dai geometri che lavoravano nella tradizione del XIX secolo, poiché permise la riscrittura di molti concetti classici della geometria differenziale in forma tensoriale. Ad esempio, Luigi Bianchi scrisse un articolo sul trasporto parallelo di Levi-Civita e pubblicò le sue idee nell’Appendice al secondo volume delle Lezioni di geometria differenziale (1923). 

L'influenza della ricerca Levi-Civita, in generale, e in particolare quella relativa al trasporto parallelo si manifestò in vari modi: i dottorandi, borsisti post-dottorato, ma anche colleghi matematici cominciarono a utilizzare i risultati; inoltre, anche attraverso la sua corrispondenza privata, le sue idee si diffusero in tutta Europa. Giovani matematici da ogni dove studiarono per un certo periodo presso Levi-Civita grazie a una borsa Rockefeller, lavorando su problemi di geometria differenziale. Levi-Civita accolse anche colleghi stranieri, come l'americano Joseph Lipka, o giovani ricercatori già in servizio, come l'irlandese Albert Joseph McConnell. I rappresentanti della scuola rumena, come George Vranceanu e Octav Onicescu, e il matematico britannico e linguista Evan Tom Davies ottennero la loro specializzazione in matematica a Roma proprio sotto la direzione di Levi-Civita. Nella seconda metà degli anni ’20, secondo l’International Education Board, Roma era considerata il terzo centro matematico europeo, dopo Parigi e Gottinga. 

A partire dagli anni ’20 la fama del matematico italiano era indiscussa, ed egli fu invitato a congressi e conferenze in tutto il mondo. Inoltre continuò a pubblicare articoli in vari settori della matematica, come la dinamica dei fluidi e, più in generale, nella matematica applicata e nella geometria differenziale. Nel 1932 e nel 1934 i prestigiosi Seminari Hadamard furono dedicati all’opera di Levi-Civita. Nel 1933 iniziò una serie di conferenze negli Stati Uniti, nel 1935 fu a Mosca, nel 1936 tornò di nuovo Oltreoceano. A Houston dichiarò la superiorità del sistema universitario americano su quello italiano. Il console italiano chiese al Governo di prendere severe misure contro di lui, ma gli fu risposto che Levi-Civita era “troppo conosciuto” per andar oltre un richiamo ufficiale. Nello stesso anno si tenne a Oslo l’undicesimo Congresso Matematico Internazionale, ma agli scienziati italiani fu vietata la presenza, perché la Norvegia era un paese che partecipava alle sanzioni contro l’Italia a seguito della guerra coloniale contro l’Etiopia. Ciò nonostante, Levi-Civita fu nominato membro della commissione che doveva assegnare le Medaglie Fields. L’ultimo ciclo di conferenze all’estero di Levi-Civita si tenne a Lima nel 1937. 

Le leggi razziali e gli ultimi anni

Nel 1938, il governo fascista aveva emanato le infami leggi razziali, che escludevano gli ebrei dall'educazione e da qualsiasi ufficio pubblico. Levi Civita, da ebreo, dovette ritirarsi e abbandonare tutte le posizioni istituzionali. Nel 1939 Francesco Severi, collega di Levi-Civita a Roma e particolarmente vicino a Mussolini, fu incaricato dall'Accademia d'Italia di organizzare il Congresso Volta dell’ottobre 1940 per la matematica, che doveva essere dedicato alla geometria differenziale. Incominciarono a partire i primi inviti agli scienziati stranieri, naturalmente dopo aver verificato attentamente che non fossero membri della "razza ebraica". È interessante vedere come Severi, con grande zelo, evitò di invitare matematici ebrei, sia in Italia che all'estero. Infatti, Levi-Civita non fu invitato. Lo stesso anno, il 4 maggio 1939, scrisse all'ex studente Vrânceanu sulle sue condizioni dopo le leggi razziali in Italia: 

"Sono in pensione e resto immobile: non in estate, tuttavia, se le condizioni generali mi consentono una certa mobilità. Come sapete, gli ebrei sono stati esclusi da qualsiasi partecipazione alla vita culturale italiana; in particolare, quindi, non parteciperò al Congresso Volta e non sarò a Roma a settembre". 

Quando il matematico olandese Jan Arnoldus Schouten, esperto in calcolo tensoriale, ricevette l'invito dell'Accademia d'Italia, rispose all'organizzatore del congresso, il 28 febbraio 1939: 

"Saranno invitati anche ebrei e parteciperanno matematici ebrei italiani? Penso in particolare al signor Levi-Civita che, come inventore del trasporto parallelo, è uno dei co-fondatori della moderna geometria differenziale. Partecipare a un congresso sulla geometria differenziale che escluda Levi-Civita per ragioni razziali sarebbe per me assolutamente inaccettabile." 

La seconda risposta a Severi arrivò dalla Francia, da Cartan, uno dei più grandi specialisti transalpini di geometria differenziale e di teoria dei gruppi di Lie. Con Schouten aveva pubblicato diversi articoli, e conosceva la lettera dell'olandese, che lo aveva inserito tra i destinatari per conoscenza. Dopo un po' di tempo decise di partecipare al Convegno, scrivendo a Severi. 

"Ho l'onore di comunicarvi il ricevimento dell'invito che mi avete fatto avere di partecipare al IX Convegno Volta che avrà luogo a Roma il prossimo ottobre. Sono molto onorato di questo invito e vi ringrazio. Parteciperò senza dubbio a questa manifestazione, salvo eventi imprevisti, e mi farà sicuramente molto piacere passare qualche giorno con i colleghi matematici di Roma". 

Non si trattava di condivisione da parte di Cartan delle leggi razziali. La lettera del francese nascondeva in realtà un desiderio: incontrare Levi Civita, che, in quanto membro anche della Pontificia Accademia delle Scienze, poté continuare in parte la sua attività. L'anno precedente l'italiano aveva inviato al francese un articolo, e Cartan gli aveva risposto con una lettera piuttosto lunga e più personale di quanto fosse sua abitudine scrivere. Eccone un brano: 

"Fubini, che ho visto recentemente [il matematico italiano di origine ebraica era transitato da Parigi prima di recarsi esule negli Stati Uniti], mi ha detto di numerosi nostri amici matematici italiani. È inutile dirvi quali siano i miei sentimenti. Spero che la signora Levi Civita e voi siate in buona salute e abbiate approfittato delle vacanze". 

Levi Civita, che aveva letto la lettera di Schouten perché era il secondo destinatario per conoscenza, rispose a Cartan dicendo: 

"[A voi vadano] Tutti i miei ringraziamenti per la simpatia che mi esprimete a seguito delle recenti manifestazioni antisemite. Fino ad ora non so nulla di ufficiale, ma ho già saputo abbastanza, o direi piuttosto troppo, dai giornali" 

Il IX Convegno Volta alla fine non si fece, perché il primo settembre era scoppiata la guerra e molti invitati dei paesi belligeranti erano impossibilitati a partecipare. 

Negli ultimi anni della sua vita, nonostante la sua depressione morale e fisica, Levi-Civita rimase fedele all'ideale dell'internazionalismo scientifico e aiutò colleghi e studenti vittime dell'antisemitismo; grazie a lui, molti di loro trovarono posti in Sud America o negli Stati Uniti. In molte lettere a lui indirizzate, il suo aiuto risulta evidente a favore di Leo Finzi, Guido Fubini, Alessandro Terracini, Berud Steinlerger e Enrico Volterra, il figlio di Vito, che era stato suo assistente dal 1933 al 1938. 

La morte di Levi-Civita il 30 dicembre 1941 fu ignorata dal mondo accademico italiano. Era stato uno dei più eminenti professori in Italia per oltre 40 anni, fu capace di creare una scuola e una tradizione e aveva attratto studenti in arrivo da tutti i paesi. Molte persone beneficiarono della sua gentilezza e conservarono un ricordo incancellabile della sua straordinaria personalità. 

La notizia della sua morte raggiunse Parigi solo nel luglio del 1942. Poiché era membro dell'Accademia di Francia, si decise di commemorarlo il 18 settembre, con un ricordo scritto proprio da Cartan. Anche in Francia erano entrate in vigore le leggi razziali, ma un ebreo morto si poteva pur ricordarlo: 

"Fu merito di Levi-Civita l’apportare un miglioramento finale [al calcolo tensoriale] con la scoperta, nel 1917, del concetto di trasporto parallelo. Rendendo più intuitive le nozioni fondamentali del calcolo differenziale assoluto [il calcolo tensoriale], egli introdusse una teoria, fino ad allora puramente analitica, nel campo della Geometria. Ne conseguirono profonde ripercussioni sullo sviluppo della Geometria stessa".

Riferimenti principali

 Le transport parallèle fête ses 100 ans

Toward a scientific and personal biography of Tullio Levi-Civita (1873–1941)

La moltiplicazione delle geometrie (3): Riemann

Un cambiamento molto significativo nella concezione stessa di geometria avvenne con l’estensione di Bernhard Riemann della geometria differenziale gaussiana. Nella tesi per l’abilitazione all'insegnamento "Sulle ipotesi che stanno alla base della geometria", presentata alla Facoltà di Filosofia di Göttingen nel 1854 e pubblicata postuma nel 1867, Bernhard Riemann (1826-1866) presentò alcune idee radicalmente innovative, con lo scopo di fornire un quadro unitario dello studio degli ambienti geometrici, dopo la scoperta delle geometrie non euclidee e utilizzando i nuovi strumenti più astratti sviluppati nel frattempo dalle varie branche della matematica. Era infatti “rimasto del tutto inesplorato il concetto generale di grandezza molteplicemente estesa, sotto cui rientrano anche le grandezze spaziali”. Egli intendeva “costruire il concetto di grandezza molteplicemente estesa a partire dal concetto generale di grandezza” e mostrare che tale concetto “era suscettibile di diverse relazioni metriche”, di cui lo spazio formava solo un caso speciale di grandezza di dimensione 3 tra tutte quelle concepibili. “I concetti di grandezza - affermava - sono possibili solo quando siamo in presenza di un concetto generale, suscettibile di diverse determinazioni. A seconda che ci sia un passaggio continuo da una determinazione a un’altra oppure no, esse formano una varietà continua o discreta.”

Riemann utilizzò per il concetto di grandezza molteplicemente estesa il termine tedesco Mannigfaltigkeit, da cui proviene il corrispondente termine inglese manifold e che noi traduciamo con varietà. Concetto polimorfo, la sua definizione dipende dall'ambiente in cui si opera, dalla natura degli elementi che lo costituiscono e dalle proprietà che si vogliono studiare. A seconda che si usino gli strumenti della sola topologia o anche quelli del calcolo differenziale e dell’analisi complessa, si parla rispettivamente di varietà topologiche, di varietà differenziabili, di varietà complesse (o analitiche), ecc.

Riemann estese a n dimensioni i metodi impiegati da Gauss (1828) nel suo studio sulla geometria intrinseca di superfici curve incorporate nello spazio euclideo (chiamate "intrinseche" perché descrivono le proprietà metriche che le superfici mostrano di per se stesse, indipendentemente dal modo in cui esse giacciono nello spazio). Il concetto di varietà generalizza quelli di curva e superficie della geometria analitica: intuitivamente, una varietà è uno spazio a più dimensioni che localmente, intorno a ogni suo punto, presenta una struttura simile a quella dello spazio euclideo, ma che globalmente può essere "curvo" ed assumere le forme più svariate.

In termini generali, un sottoinsieme X⊂Rⁿ è una varietà di dimensione m (con m ≤ n) se, nell'intorno dei suoi punti, esso assomiglia ad un aperto di R^m. Le varietà localmente simili alla retta R si chiamano curve, mentre quelle localmente simili al piano R² si chiamano superfici. Se una varietà X è localmente simile a Rⁿ, allora si definisce X una varietà di dimensione n.

Riemann notò che le proprietà misurabili di una varietà discreta, di cui è facile trovare esempi in natura, possono essere facilmente determinate contando. Ma le varietà continue, che ricorrono con grande frequenza in matematica, non ammettono questo approccio. In particolare, le proprietà misurabili dello spazio fisico, che sono l’oggetto della geometria, fino ad allora erano state verificate con successo in accordo con la geometria euclidea: la distanza tra due punti nello spazio può essere accertata con un'asta, o un nastro, o con mezzi ottici, e il risultato dipende essenzialmente dal comportamento fisico degli strumenti utilizzati. Tuttavia, "i concetti empirici su cui si basano le determinazioni metriche dello spazio - i concetti di un corpo rigido e di un raggio di luce - perdono la loro validità nell'infinitamente piccolo; è quindi molto probabile che le relazioni metriche dello spazio nell'infinitamente piccolo non siano in accordo con le assunzioni della geometria, e infatti dovremmo accettarlo non appena i fenomeni potranno essere così spiegati in un modo più semplice”. Si trattava di una considerazione a suo modo profetica.

Lo schema di base di Riemann ambiva a una generalità molto più ampia, ma, a suo giudizio, doveva essere sufficiente per il momento caratterizzare la geometria delle varietà continue in modo tale che fosse perfettamente in accordo con la geometria euclidea su un piccolo intorno di ciascun punto. Ad esempio, localmente la superficie terrestre somiglia ad un piano, e per questo è una varietà di dimensione 2. Tuttavia tale somiglianza non conserva la distanza tra i punti, in quanto la sfera ha una curvatura diversa. La curvatura incide sulla somma degli angoli interni di un triangolo: nel piano tale somma è sempre 180°, mentre su una sfera è sempre maggiore. La superficie della Terra non è descrivibile interamente su un foglio (nel senso che non è omeomorfa ad un aperto di R²), però è possibile descriverla "a pezzi" tramite un certo numero di carte geografiche. Ogni mappa di un atlante terrestre è costituita da intorni di punti della superficie omeomorfi al piano, Le mappe non formano una tassellatura perfetta e si sovrappongono parzialmente l’una con l’altra, tuttavia è possibile orientarsi grazie alle coordinate geografiche dei punti. Analogamente, una varietà può essere descritta da una serie di funzioni continue (carte) che nel loro insieme costituiscono un atlante. Partendo da una lista di spazi considerati “semplici”, per ogni punto della varietà si considera un intorno omeomorfo a uno spazio semplice, che costituisce una carta. Nell'intersezione tra intorni, le carte si possono comporre generando funzioni tra spazi semplici dette funzioni di transizione. Queste ultime devono essere compatibili, cioè devono essere come minimo omeomorfismi, ma spesso si richiede che siano differenziabili.

Notando come su una stessa varietà si possono definire in modi diversi le distanze tra due punti (dipende dalla scelta della funzione), Riemann concludeva che “c’è tuttavia una differenza essenziale tra rapporti metrici e di estensione”, che diventava fondamentale quando “si estendono le costruzioni dello spazio allo smisuratamente grande”. In tal caso “bisogna fare distinzione tra l’illimitato e l’infinito: il primo appartiene ai rapporti di estensione, il secondo ai rapporti metrici”. Con questa preziosa osservazione si affacciava la possibilità, sfuggita ai geometri prima di lui, di una geometria ellittica, che è la geometria della superficie di una sfera, in cui viene meno non solo il postulato delle parallele, ma anche quello dell’infinità della retta. Una retta in questa geometria corrisponde sempre e comunque a uno dei cerchi massimi della sfera: nella geometria ellittica di Riemann quindi non esistono parallele, in quanto ogni coppia di rette converge in punti antipodali. Quando la curvatura dello spazio assume un valore positivo, per quanto piccolo, lo spazio “sarebbe necessariamente finito”.

Non vi era alcun bisogno che una geometria riemanniana n-dimensionale dovesse essere ottenuta da una mappa di un sottoinsieme n-dimensionale di un qualche spazio euclideo. Ciò significava che si può fare geometria senza riferimento a quella euclidea: la geometria euclidea non veniva più epistemologicamente prima di qualsiasi studio di altre geometrie. Le idee su come la geometria teoretica di qualsiasi tipo si relazionasse con lo spazio intorno a noi erano diventate molto più sofisticate. La verità della geometria non era più da dare per scontata, ma era diventata in qualche misura empirica, e anche le idee filosofiche sull'intelligibilità della geometria si erano approfondite. Esistevano migliori sistemi formali e assiomatici. Il regno di Euclide era teoricamente finito.