Diagrammi di fase

 

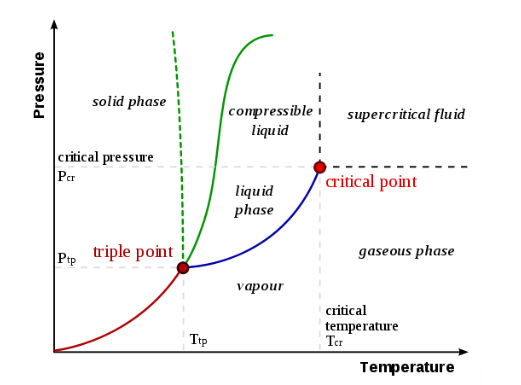
Un diagramma di fase è una rappresentazione grafica degli stati fisici di una sostanza in diverse condizioni, solitamente di temperatura e pressione, ma si possono considerare altre variabili di stato. Un tipico diagramma di fase ha la pressione sull'asse y e la temperatura sull'asse x. Quando attraversiamo le linee o le curve del diagramma di fase, si verifica un cambiamento di fase. Inoltre, due stati della sostanza coesistono in equilibrio sulle linee o curve. Ecco un esempio di diagramma di fase per un sistema monocomponente generico:

Figura 1. Diagramma di fase generico

Le etichette sul grafico rappresentano gli stati stabili di un sistema in equilibrio. Le linee rappresentano le combinazioni di pressioni e temperature alle quali possono esistere due fasi in equilibrio. In altre parole, queste linee definiscono i punti di cambiamento di fase. La linea rossa divide le fasi solida e gassosa, rappresenta la sublimazione (da solido a gas) e il brinamento (da gas a solido). La linea verde divide le fasi solida e liquida e rappresenta la fusione (da solido a liquido) e la solidificazione (da liquido a solido). Il blu divide le fasi liquida e gassosa, rappresenta l’evaporazione (da liquido a gas) e la condensazione (da gas a liquido). Ci sono anche due punti importanti nel diagramma, il punto triplo e il punto critico. Il punto triplo rappresenta la combinazione di pressione e temperatura che facilita tutte le fasi della materia all'equilibrio. Il punto critico determina l'insieme di particolari condizioni di massima temperatura e massima pressione in corrispondenza delle quali una sostanza può esistere come miscela bifase gas-liquido. Oltre tale punto non si parla più di gas e liquido, bensì di fluido supercritico.

Nella maggior parte delle sostanze, la temperatura e la pressione relative al punto triplo si trovano al di sotto della temperatura e pressione standard e la pressione per il punto critico è al di sopra della pressione standard. Pertanto, alla pressione standard, all'aumentare della temperatura, la maggior parte delle sostanze cambia da solida a liquida in gas, e, alla temperatura standard, all'aumentare della pressione, la maggior parte delle sostanze cambia da gas a liquido a solido.

Figura 2a: Diagramma di fase per la CO₂

Normalmente la linea della fase solido/liquido ha una pendenza positiva verso destra (come nel diagramma per l'anidride carbonica). Tuttavia, per altre sostanze, in particolare l'acqua, la linea è inclinata verso sinistra, come mostra il diagramma per l'acqua. Ciò indica che la fase liquida è più densa della fase solida. Questo fenomeno è causato dalla struttura cristallina della fase solida. Nelle forme solide dell'acqua e di alcune altre sostanze, le molecole cristallizzano in un reticolo con uno spazio medio maggiore tra le molecole, risultando così un solido con una densità inferiore rispetto al liquido. A causa di questo fenomeno, si può sciogliere il ghiaccio semplicemente applicando pressione e non aggiungendo calore.

Figura 2b: Diagramma di fase per l’H₂O

Muoversi all’interno del diagramma di fase fornisce informazioni sulle fasi della sostanza presa in esame. Lo spostamento lungo una linea di temperatura costante rivela le densità relative delle fasi. Quando ci si sposta dalla parte inferiore del diagramma verso l'alto, la densità relativa aumenta. Muoversi lungo una linea di pressione costante rivela le energie relative delle fasi. Quando ci si sposta da sinistra a destra del diagramma, aumentano le energie relative.

I diagrammi di fase e i sistemi che descrivono sono spesso classificati e denominati in base al numero (in latino) di componenti del sistema illustrato nella tabella 1. Chiaramente, all'aumentare del numero di componenti, aumenta anche il numero di sistemi possibili (tabella 2).

Tabella 1. Classificazione dei diagrammi di fase e dei sistemi

Fonte: Massalski (1998)

Tabella 2. Possibile numero di sistemi (n = numero di elementi (diciamo 90); m = numero di elementi in un sistema).

La tabella mostra che anche se si scelgono solo quattro componenti da un gruppo di, diciamo, 90 elementi, il numero possibile di combinazioni raggiunge milioni, il che ci dice che i diagrammi di fase dei sistemi quaternari sono molto lontani dall'essere determinati, a meno che possano essere calcolati tramite un programma utilizzando stime delle energie libere.

La classificazione e i limiti dei cambiamenti di fase sono descritti dalla regola delle fasi, proposta dal chimico americano J. Willard Gibbs nel 1876 e basata su una rigorosa relazione termodinamica. La regola delle fasi in un sistema con 2 variabili non composizionali (P e T) è comunemente data nella forma P + F = C + 2. La lettera P si riferisce al numero di fasi presenti all'interno del sistema, C è il numero minimo di componenti chimici indipendenti necessari per descrivere la composizione di tutte le fasi del sistema. Il termine F, chiamato varianza, o grado di libertà, descrive il numero minimo di variabili che devono essere fissate per definire una particolare condizione del sistema.

"I diagrammi di fase sono l'inizio della saggezza, non la sua fine". Questa famosa citazione di Sir William Hume-Rothery è una linea guida perfetta per qualsiasi lavoro di scienza e tecnologia dei materiali. I diagrammi di fase sono la mappa migliore per comprendere le condizioni per la formazione o la trasformazione di fase in qualsiasi sistema materiale causata da variazioni di temperatura, composizione, pressione o qualsiasi altra variabile di stato importante. Ecco perché è possibile utilizzare i diagrammi di fase come punto di partenza per la progettazione dei materiali e l'ottimizzazione del processo manipolando la composizione e le variabili di elaborazione per ottenere la microstruttura desiderata. Ciò vale per tutti i tipi di materiali, come leghe, ceramiche, semiconduttori, calcestruzzo, ecc., e per una moltitudine di processi, come fusione, colata, crescita dei cristalli, giunzione, trattamento termico/trasformazione di fase, ossidazione, deposizione di vapore e così via.

La figura 3 mostra il diagramma di fase del ferro puro. Si tratta di un sistema unario, costruito da un singolo componente. Gli assi sono le variabili di stato temperatura T e pressione P, la pressione è mostrata in scala logaritmica per rivelare la regione della fase gassosa insieme alla parte ad alta pressione. Tutte le aree nel diagramma hanno un significato, come si vede dall'esempio seguente. Consideriamo il punto di stato a 1000 K e 103 bar, indicato dal mirino in Fig. 3. Cioè, mettiamo una certa quantità di Fe puro in una scatola chiusa e fissiamo la temperatura e la pressione a questi valori. Ora, gli atomi di Fe possono organizzarsi in varie fasi, come Gas, Liquido, BCC (reticolo cubico compatto), FCC (reticolo cubico a facce centrate) o HCP (reticolo esagonale compatto). Ogni fase ha un valore unico di energia di Gibbs, G (T, P), in quel dato punto di stato. La fase con il valore più basso di energia G di Gibbs è la “vincitrice”; è la fase stabile nella condizione data. In questo caso, è la fase BCC (α). In altre parole, questa è la regione monofase stabile della fase BCC (α) e in qualsiasi punto dello stato in questa regione il valore di energia di Gibbs di qualsiasi fase concorrente è superiore a quello della fase BCC (α). La stessa regola di concorrenza si applica a tutti i punti di stato nell'intero diagramma di fase in Fig. 3 che compone le regioni monofase di Gas, Liquido, BCC (δ), FCC (γ), BCC (α) e HCP. Se si sceglie di utilizzare altre variabili di stato diverse da T e P, altre funzioni termodinamiche invece dell'energia di Gibbs devono essere ridotte al minimo per trovare il campo stabile di ciascuna fase.

Fig. 3: Diagramma di fase del ferro puro. Un punto di stato (103 bar, 1000 K) è contrassegnato dal mirino

La linea di confine tra le regioni BCC (α) e FCC è definita dall'uguaglianza dei valori energetici di Gibbs, G BCC (T, P) = G FCC (T, P). Tale linea non solo rivela la dipendenza dalla pressione della temperatura di trasformazione di fase BCC (α)/FCC, ma forma anche la regione a due fasi BCC (α) + FCC nel diagramma di fase. Tutte queste regioni a due fasi in Fig. 3 sono linee unidimensionali a causa della scelta delle variabili di stato, T e P, per tracciare questo diagramma. La regione trifase BCC (α) + FCC + HCP si verifica solo in un punto di stato unico, 757 K e 105,019 bar nel diagramma di fase. Pertanto, questo è un equilibrio invariante, il punto triplo. I gradi di libertà sono zero ad un equilibrio invariante secondo la regola della fase di Gibbs. Ciò significa che non è possibile modificare alcuna variabile di stato (T o P) senza perdere una fase dall'equilibrio. Al contrario, l'equilibrio a due fasi BCC (α) + FCC in Fig. 3 è monovariante, ha un grado di libertà. Una variabile può essere modificata, almeno in modo infinitesimale, e regolando l'altra lungo la relativa linea T–P si può mantenere l'equilibrio BCC (α) + FCC. Quando si tracciano i diagrammi di fase con la scelta di diverse variabili di stato come assi (es. entalpia anziché temperatura) la topologia delle regioni bifase e trifase può cambiare in modo che non siano più monodimensionali o zero-dimensionali.

La rilevanza geofisica del diagramma di fase del ferro è che aiuta a spiegare perché il nucleo interno della nostra terra è solido. Ciò è caratteristico, perché la temperatura aumenta fino al centro della terra in modo che il nucleo esterno, composto principalmente da una lega ferro-nichel, è liquido. Tuttavia, scendendo più in basso, la lega si solidifica al confine con il nucleo interno, anche se la temperatura continua ad aumentare. Ciò è dovuto al continuo aumento della pressione, che si traduce in un drammatico aumento della temperatura di fusione, mostrato per il Fe puro in Fig.3. La pressione al confine è di circa 330 GPa, o 3,3 × 10⁶ bar, appena fuori dal campo di Fig.3, e la temperatura di fusione della lega ricca di Fe a questa pressione è stimata in 5600 K. L'ulteriore aumento della pressione solidifica la lega.

L'importanza industriale dell'acciaio deriva fondamentalmente da una particolarità del diagramma di fase in Fig. 3, la presenza di due regioni separate di BCC, una ad alta temperatura BCC (δ), e una a bassa temperatura, BCC (α). Normalmente i cristalli FCC più densamente impacchettati dovrebbero essere stabili fino a temperatura ambiente. Tuttavia, i cristalli di ferro BCC meno densamente impacchettati subiscono un ordinamento magnetico, che diminuisce significativamente i valori di G BCC (T), rendendo nuovamente stabile la fase BCC a temperature più basse. Ciò si traduce nel verificarsi della transizione di fase γ/α del ferro, che può essere modificata e adattata mediante l'aggiunta di carbonio e altri elementi di lega nell'acciaio. La corretta progettazione di questa transizione di fase allo stato solido γ/α costituisce la base per il controllo della varietà di microstrutture nell’acciaio, dalla struttura come colata al trattamento termico o alla lavorazione termomeccanica. Senza la transizione FCC (γ)/BCC (α) in Fig. 3 a pressione ambiente l'uomo non potrebbe produrre acciaio.

Tutte le fasi nella Figura 4 hanno la stessa composizione, quella del biossido di silicio, SiO₂. Le fasi coesite, quarzo α, quarzo β, tridimite e cristobalite sono fasi solide composte da biossido di silicio; ognuno ha la propria disposizione atomica e un insieme distintivo di proprietà fisiche e chimiche. La forma più comune di quarzo (che si trova nelle sabbie e nei graniti delle spiagge) è il quarzo α. La regione fusa anidra rossa è costituita da biossido di silicio liquido.

Figura 4: Diagramma di fase del biossido di silicio

Diverse porzioni del sistema di biossido di silicio possono essere esaminate in termini della regola di fase. Nel punto A esiste un'unica fase solida: quarzo α. Sostituendo i valori appropriati nella regola di fase P + F = C + 2 si ottiene 1 + F = 1 + 2, quindi F = 2. Per il punto A (o qualsiasi punto in cui una sola fase è stabile) il sistema è bivariante: cioè esistono due gradi di libertà. Pertanto, le due variabili (pressione e temperatura) possono essere modificate indipendentemente e lo stesso insieme di fase continua ad esistere.

Il punto B si trova sulla curva di confine tra i campi di stabilità del quarzo α e del quarzo β. In tutti i punti lungo questa curva, queste due fasi coesistono. Sostituendo i valori nella regola di fase (2 + F = 1 + 2) si otterrà una varianza pari a 1. Ciò indica che una variabile indipendente può essere modificata in modo tale da mantenere la stessa coppia di fasi. Una seconda variabile deve essere modificata per conformarsi alla prima in modo che l'assemblaggio di fase rimanga sul confine tra quarzo α e β. Lo stesso risultato vale per le altre curve limite in questo sistema.

Il punto C si trova in un punto triplo, condizione in cui si intersecano tre campi di stabilità. La regola di fase (3 + F = 1 + 2) indica che la varianza è 0. Il punto C è quindi un punto invariante; una variazione di pressione o di temperatura comporta la perdita di una o più fasi. La regola delle fasi rivela inoltre che non più di tre fasi possono coesistere stabilmente in un sistema a un componente perché fasi aggiuntive porterebbero a una varianza negativa.

Tutti gli altri diagrammi di fase P-T unari o monocomponenti possono essere compresi seguendo gli esempi forniti. Le regole e la topologia risultanti sono identiche se il componente è un elemento o una sostanza pura, definita come un composto che non può cambiare composizione.

Esistono molti altri composti stechiometrici solidi con un intervallo di soluzione solida trascurabile o una deviazione stechiometrica trascurabile, che formano una sostanza solida pura. Alla fusione, tuttavia, la composizione spesso non viene mantenuta. È ad esempio il caso del carburo di silicio, SiC, un importante composto semiconduttore e anche un importante materiale ceramico. Riscaldando SiC a 1 bar sopra 2830 °C si ottiene una fase liquida ricca di silicio con solo il 19% di C e in aggiunta una certa quantità di grafite, bilanciando così l'originale 50% di SiC. Cioè, il cristallo di SiC monofase si decompone in un liquido e grafite, con un processo chiamato di fusione incongruente. Questo è un equilibrio a tre fasi, non una semplice fusione a due fasi. Nel diagramma di fase P-T del SiC a 1 bar la regione monofase del SiC solido termina a 2830°C, oltre uno spazio vuoto si forma la regione bifase liquido + grafite. Il calcolo mostra che è necessaria una temperatura di 3600°C (e una pressione di almeno 8 bar per evitare l'evaporazione) per ottenere "SiC" liquido monofase con 50% di C. Questo ampio gap di 790 K, liquido + grafite, nel "diagramma di fase P-T di SiC" si verifica perché, tecnicamente parlando, è una sezione nel diagramma di fase P-T-x del sistema binario Si-C a 50% costante di C.

Figura 5: Diagramma di fase del carburo di silicio in ragione della percentuale di Si e C

Pertanto, il composto SiC non può essere ben rappresentato da un diagramma di fase P-T unario, a differenza del composto H₂O. Affinché la topologia semplice di Fig. 1, osservata per qualsiasi elemento, prevalga anche per un composto, è necessario che questo composto esista in tutte le fasi in tutte le condizioni (in tutti i punti di stato) come monofase stabile, realizzando tutte le transizioni di fase congruenti. In caso contrario, la topologia del diagramma di fase P-T sarà più complessa. L'importante distinzione tra proprietà e diagramma di fase, tuttavia, è generalmente valida e deve essere tenuta presente anche per sistemi multicomponente.

Isostasia, quando le rocce galleggiano

 

L’isostasia ė l’equilibrio teorico ideale di tutte le grandi porzioni della litosfera terrestre, come se galleggiassero sullo strato sottostante più denso, la astenosfera, una sezione del mantello superiore composta da roccia più fluida, che si trova a circa 110 km sotto la superficie. L'isostasia controlla le elevazioni regionali dei continenti e dei fondali oceanici in accordo con la densità delle loro rocce sottostanti. Si presume che colonne immaginarie di uguale area di base che salgono dall'astenosfera alla superficie abbiano pesi uguali ovunque sulla Terra, anche se i loro costituenti e le elevazioni delle loro superfici superiori sono significativamente diversi. Ciò significa che un eccesso di massa visto al di sopra del livello del mare, come accade in un sistema montuoso, è dovuto a un deficit di massa, o radici a bassa densità, al di sotto del livello del mare. Pertanto, le alte montagne hanno radici a bassa densità che si estendono in profondità nel mantello sottostante. Il concetto di isostasia ha svolto un ruolo importante nello sviluppo della teoria della tettonica a zolle. 

Nascita della teoria - Nel 1735, l’astronomo Pierre Bouguer (1698-1758), durante una spedizione francese sulle Ande per misurare la lunghezza dell'arco meridiano ad un grado di latitudine vicino all'equatore, fu il primo a misurare l'attrazione gravitazionale orizzontale delle montagne, notando che le Ande non potevano rappresentare una protuberanza di roccia collocata su una piattaforma solida. In tal caso, un filo a piombo avrebbe dovuto essere deviato dalla vera verticale di una quantità proporzionale all'attrazione gravitazionale della catena montuosa. La deviazione era invece inferiore a quella prevista. Un resoconto completo delle sue osservazioni fu pubblicato nel 1749 con il titolo La figure de la terre. 

Circa un secolo dopo, simili discrepanze furono osservate da Sir George Everest, geometra generale dell'India, nelle indagini a sud dell'Himalaya, indicando una mancanza di massa compensativa al di sotto delle catene montuose. Anche Everest si aspettava che la massa gravitazionale dell'Himalaya avrebbe causato deviazioni nei fili a piombo, ma osservò che essi non erano deviati verso le montagne quanto ci si poteva aspettare. In effetti la differenza avrebbe dovuto essere maggiore. 

Il primo tentativo di spiegazione del fenomeno tentò di darla nel 1855 il matematico inglese e missionario anglicano in India John Henry Pratt (1809-1871), che postulò differenze di densità nella crosta terrestre, densità più basse sotto le montagne, densità più elevate in pianura, per spiegare i valori (quasi costanti) ottenuti per la gravità a una data latitudine. L'ipotesi di Pratt presupponeva che la crosta terrestre avesse uno spessore uniforme sotto il livello del mare, con una base che a una determinata profondità regge un peso uguale per unità di area. In sostanza, la sua teoria sosteneva che le aree della Terra di densità minore, come le catene montuose, sporgono più in alto sul livello del mare rispetto a quelle di densità maggiore. La spiegazione di ciò era che le montagne risultavano dall'espansione verso l'alto di materiale crostale riscaldato localmente, che aveva un volume maggiore ma una densità inferiore dopo essersi raffreddato. 

Sir George Biddell Airy (1801-1892), matematico e astronomo inglese, a lungo Astronomo Reale, nello stesso anno ipotizzava invece che la crosta avesse una densità uniforme dappertutto. Lo spessore dello strato crostale non è però uniforme, e quindi la sua teoria ipotizzava che le parti più spesse della crosta affondassero più in profondità nel substrato, mentre le parti più sottili ne fossero sostenute. Secondo questa ipotesi, le montagne hanno radici sotto la superficie che sono molto più grandi della loro espressione superficiale. 

L'ipotesi di Airy, oggi considerata più vicina alla realtà, afferma che la crosta terrestre è un guscio più rigido che galleggia su un substrato più liquido di maggiore densità. In pratica le montagne si comportano come un iceberg che galleggia sull'acqua, in cui la maggior parte dell'iceberg è sommerso. 

Teoria di Pratt (a sinistra) e di Airy (a destra) 

Entrambe le teorie si basano sulla presunta esistenza di uno strato fluido o plastico più denso, l’astenosfera, su cui galleggia la litosfera rocciosa. A metà del XX secolo, con l'analisi dei terremoti, è stato verificato che essa è presente ovunque sulla Terra: le onde sismiche, la cui velocità diminuisce con la fluidità del mezzo, passano più lentamente attraverso di essa. Sia le proposte di Pratt che quelle di Airy hanno storicamente avuto i loro pregi, ma sono semplificazioni eccessive della situazione reale. 

Ancora non esisteva il termine isostasia (gr. ἴσος "uguale", στάσις "posizione"), che fu coniato dal geologo americano Clarence Dutton (1841-1912), che in una nota a piè di pagina di una recensione del 1882 sull'American Journal of Science, scrisse: 

"In un articolo inedito ho usato i termini isostatico e isostacia (sic) per esprimere quella condizione della superficie terrestre che deriverebbe dal galleggiamento della crosta su un substrato liquido o altamente plastico - porzioni diverse della crosta essendo di densità disuguale". 

Dutton illustrò queste idee nel suo discorso alla Philosophical Society di Washington nel 1889. Quando questo fu stampato nel 1892 fu proposto formalmente il termine isostasia, dopo che Dutton, su consiglio dei grecisti, corresse la "c" in una "s". 

Una volta accettato il concetto di isostasia, si voleva stabilire a quale profondità si trova la superficie sulla quale “galleggiano” i blocchi di crosta terrestre. Agli inizi del Novecento la ricerca della “profondità di compensazione” fu una sfida intrapresa dai geologi americani John Fillmore Hayford (1868-1925) e William Bowie (1872-1940) dell’US Coast and Geodetic Survey. 

La teoria di Hayford ipotizza che ci debba essere una distribuzione compensativa di materiali rocciosi di densità variabile in modo che la crosta terrestre eserciti una pressione essenzialmente uniforme a una certa profondità all'interno della Terra. Da studi sulle anomalie gravitazionali in vari luoghi, Hayford stimò che la profondità della compensazione isostatica variasse da 60 a 122 km (da 37 a 76 miglia) e da ciò dedusse la figura geometrica della Terra, che fu adottata nel 1924 come Ellissoide Internazionale dalla International Geodetic and Geophysical Union. 

Bowie coordinò osservazioni sistematiche delle anomalie gravitazionali sulla terraferma e incoraggiò indagini gravitazionali negli oceani. Queste osservazioni mostrarono che le anomalie erano correlate con le caratteristiche topografiche e convalidarono l'isostasia come fenomeno geologico. Con Hayford calcolò le tabelle della profondità della compensazione isostatica, considerandola in media pari a 113 km (70 miglia). Il suo libro Isostasy fu pubblicato nel 1927. 

A causa dei cambiamenti degli ambienti tettonici, tuttavia, l'isostasia perfetta viene raramente raggiunta e alcune regioni, come le fosse oceaniche e gli altipiani, non sono compensate isostaticamente. L'equilibrio isostatico è uno stato ideale in cui la crosta e il mantello si stabilizzerebbero in assenza di forze di disturbo. L'aumento e lo scioglimento delle calotte glaciali, l'erosione, la sedimentazione e il vulcanismo effusivo sono esempi di processi che perturbano l'isostasia. Le proprietà fisiche della litosfera (il guscio roccioso che forma l'esterno della Terra) sono influenzate dal modo in cui il mantello e la crosta rispondono a queste perturbazioni. Pertanto, la comprensione della dinamica dell'isostasia aiuta a capire fenomeni più complessi come la formazione di montagne e bacini sedimentari, la disgregazione dei continenti e la formazione di nuovi bacini oceanici. 

Misure di gravità - Poiché l'isostasia prevede carenze di massa nelle regioni più elevate, un modo per testare l'isostasia su scala planetaria è misurare la variazione del campo gravitazionale locale. Un semplice pendolo può essere utilizzato per misurare la forza di gravità locale: in effetti, fu così che furono eseguite le prime misurazioni della gravità. Al giorno d'oggi, la geodesia fisica, lo studio delle proprietà fisiche del campo gravitazionale terrestre, utilizza i gravimetri relativi e assoluti per le indagini gravitazionali. I moderni gravimetri assoluti sono interferometri ottici a laser che misurano in un punto l’accelerazione di una massa in caduta libera nel vuoto. L’unità di misura solitamente utilizzata per le misurazioni è il milligal (mGal), che vale 10^-5 m/s². La precisione di questi strumenti è dell’ordine del microgal, cioè 1 x 10^-8 m/s². I gravimetri relativi, che misurano la differenza di gravità esistente fra due punti, utilizzano principalmente molle al quarzo a lunghezza zero e sono calibrati sui gravimetri assoluti. 

A causa della rotazione, la Terra è più schiacciata ai poli e sporge all'equatore, formando all'incirca un ellissoide; quindi, al livello del mare il valore della gravità dipende dalla latitudine ed è inferiore alle latitudini vicine all'equatore che alle latitudini vicine ai poli. Questo valore di gravità in un punto particolare dell'ellissoide è chiamato valore teorico per quel punto. 

Varie formule, successivamente più raffinate, per il calcolo della gravità teorica sono indicate come International Gravity Formula, la prima delle quali fu proposta nel 1930 dall'International Association of Geodesy. Una formula teorica più recente per la gravità in funzione della latitudine è la International Gravity Formula 1980 (IGF80), basata sull'ellissoide standard di riferimento WGS80, che utilizza l'equazione di Somigliana (dal nome del fisico matematico italiano Carlo Somigliana, 1860-1955, che la propose nel 1929):

dove:

g(φ) è la gravità in funzione della latitudine geografica φ della posizione di cui si vuole determinare la gravità; 

k è una costante di formula; 

g_e, è la gravità all'equatore; 

a, b sono rispettivamente i semiassi equatoriali e polari dello sferoide; 

e² = (a²-b²) / a² è l’eccentricità quadrata dello sferoide; 

da cui: 

Sottraendo il valore teorico della gravità g(φ) dal valore osservato della gravità g’ in un punto, si ottiene una differenza chiamata anomalia gravitazionale. Dopo aver corretto con varie tecniche sia la quota che l'attrazione gravitazionale delle rocce tra lo strumento e l'ellissoide, il valore misurato della gravità meno il valore teorico viene detto anomalia di gravità di Bouguer. 

Poiché il valore teorico viene determinato ipotizzando che la densità sia omogeneamente distribuita al di sotto della superficie terrestre secondo involucri concentrici, se risulta che il valore misurato g’ è maggiore di quello teorico g(φ) (anomalia gravimetrica positiva) vuol dire che la densità delle rocce nel sottosuolo in quel punto è maggiore di quanto previsto teoricamente. Se, al contrario, si registra che il valore misurato è minore di quello teorico (anomalia gravimetrica negativa), si conclude che nel sottosuolo si trovano masse rocciose più leggere di quelle previste teoricamente. Questo tipo di ricerche è utilizzato a livello locale nel campo della prospezione mineraria. 

Le misurazioni del campo gravitazionale terrestre indicano che le anomalie gravitazionali di Bouguer sono generalmente molto negative sulle montagne e altipiani e nulle o positive sugli oceani. La gravità è infatti più debole su gran parte delle Alpi, dell'Himalaya e di molte altre catene montuose. Le anomalie tipiche delle Alpi centrali sono dell'ordine di −150 milligal. Nelle regioni che hanno avuto il tempo di raggiungere l'equilibrio isostatico senza essere disturbate da altri effetti geologici, come il sud-ovest degli Stati Uniti, esiste un'ottima correlazione tra la quota e le anomalie gravitazionali di Bouguer, fornendo prove convincenti per l'isostasia. 

Le leggi dell’isostasia agiscono sui continenti proprio come farebbero sugli iceberg e sulle zattere. Un iceberg si alzerà più fuori dall'acqua quando la parte superiore si scioglie e una zattera affonda più in profondità quando vengono aggiunti carichi. Tuttavia, il tempo di adattamento per i continenti è molto più lento, a causa della viscosità dell'astenosfera. Ciò si traduce in molti processi geologici dinamici che si osservano oggi. L’esempio più noto è dato dall’isostasia glaciale. 

Isostasia glaciale - L'isostasia glaciale è il processo mediante il quale la litosfera terrestre viene pressata dal peso di una calotta glaciale. Quando la massa di ghiaccio viene successivamente ridotta o rimossa e il peso viene tolto, ciò consente alla crosta di risalire e tornare alla sua posizione originale. La quantità di depressione crostale risultante del carico della calotta glaciale è una funzione dello spessore del ghiaccio e del rapporto tra la densità del ghiaccio e della roccia. La densità del ghiaccio è circa un terzo di quella della crosta, e quindi la depressione crostale sotto una calotta glaciale è circa un terzo dello spessore del ghiaccio. Una calotta di ghiaccio di mille metri di spessore ha la capacità di abbassare il terreno sottostante di 275 m. Normalmente, la quantità di depressione crostale aumenta dal margine verso il centro della calotta glaciale, dove nella maggior parte dei casi le calotte glaciali sono più spesse. Attualmente, in Antartide, il peso della calotta glaciale è così elevato che ha abbassato il continente di 1 km nella crosta terrestre. Se queste masse di ghiaccio dovessero sciogliersi, anche la terra sottostante subirebbe un rimbalzo isostatico.

Occorrono diverse migliaia di anni prima che avvenga l'adeguamento isostatico perché c'è un intervallo di tempo tra la ritirata del ghiacciaio e la risposta della crosta terrestre. Quando una calotta glaciale inizia a ridursi, sollevando il peso dalla massa continentale depressa, inizia il processo di rimbalzo, iniziando rapidamente, per poi rallentare. 

Ci sono prove del rimbalzo isostatico nel passato. Nel Mar Baltico e nell'area della Baia di Hudson vicino al Canada, che erano entrambi ricoperti da una calotta glaciale 14mila anni fa, esistono oggi antiche linee di spiaggia a circa 300 m sotto il livello del mare. Gli scienziati della NASA e del Servizio Geologico americano ritengono che quest'area stia ancora attivamente risalendo, ma a un ritmo molto più lento rispetto a poco dopo l'ultima era glaciale. Affinché la Baia di Hudson raggiunga il suo stato di "equilibrio", i geologi calcolano che debba ancora risalire di circa 150 m. Il sottosuolo del Mar Baltico settentrionale (Golfo di Botnia) sale di circa 1 cm all’anno. 

Per quanto riguarda il riscaldamento globale, l'isostasia glaciale entra in gioco quando si calcola l'innalzamento del livello del mare per lo scioglimento delle calotte glaciali e per l'espansione termica dell'acqua. In alcuni casi, l'isostasia può compensare alcuni degli effetti dell'innalzamento del livello del mare. Il problema, tuttavia, è che l'isostasia progredisce più lentamente dell'innalzamento del livello del mare, per cui la compensazione degli effetti negativi sarebbe minima. 

Nel periodo dell'ultimo massimo glaciale, il volume delle calotte glaciali ha prodotto un abbassamento del livello del mare di circa 120-130 m. Al contrario, lo scioglimento delle calotte glaciali della Groenlandia e dell'Antartico causerebbe un innalzamento del livello del mare rispettivamente di 5,5 e 60 m (innalzamento globale medio del livello del mare di circa 70 m: vedi in figura la proiezione per l’Europa). Non sarebbe un bell'affare per le aree costiere, dove vive circa il 40% della popolazione mondiale.

La metrica dell’interno della Terra

La soluzione di un problema geometrico consentirebbe di determinare la struttura di un oggetto da informazioni limitate, forse

Un problema inverso consiste nel determinare le caratteristiche fisiche di un oggetto inaccessibile alla misura mediante lo studio della sua risposta a una stimolazione ondulatoria. Detto in altro modo, l’osservatore controlla una sorgente che produce delle onde (un fascio laser, ad esempio) che interagiscono con l’oggetto in questione e il cui comportamento – come l’angolo di deviazione della luce prodotta – fornisce informazioni sulla struttura dell’oggetto.

Che un oggetto non sia osservabile immediatamente, cioè tramite il semplice ricorso a uno strumento d’osservazione come un telescopio, è forse la caratteristica principale della fisica moderna e, in questo senso, ogni problema fisico riguardante l’infinitamente piccolo o l’infinitamente grande potrebbe essere definito come problema inverso. Se Rutherford scoprì nel 1909 il modello planetario dell’atomo, demolendo il modello precedente di Thomson, secondo il quale un atomo era costituito dal solo nucleo contenente le due cariche opposte, non è stato osservando la struttura atomica attraverso un microscopio super-potente, ma è stato studiando la debole deviazione delle particelle alfa (che, si scoprirà poi, sono assimilabili a delle onde) bombardando un sottile foglio d’oro. Rutherford scoprì in questo modo la struttura lacunosa della materia, rivelando l’esistenza di un nucleo carico positivamente e degli elettroni, carichi negativamente, che gravitano attorno a quest’ultimo in un “vasto” volume.

Di conseguenza, la maggior parte dei progressi nella fisica del XX secolo si è basata sull'osservazione di eventi che sono conseguenze dell'esistenza stessa degli oggetti. In altre parole: la conferma dei modelli teorici è stata fatta osservando gli effetti che prevedevano, non gli oggetti che esse consideravano in quanto tali. L'esempio più significativo che può essere menzionato è certamente quello dei buchi neri. La teoria della relatività generale - che cerca di comprendere i fenomeni di gravitazione delle stelle - predice l'esistenza di oggetti celesti così compatti e densi, i buchi neri, che la loro forza di attrazione gravitazionale impedisce a qualsiasi raggio di luce di sfuggire. Per sua natura, un buco nero non può essere visto, perché nessuna luce da essi può raggiungerci. Per quanto paradossale possa essere, gli astronomi sono ora in grado di prevedere l'esistenza di un buco nero e persino di localizzarlo, grazie a varie tecniche, come l'osservazione delle lenti gravitazionali, cioè. la forte deviazione della luce (un'onda) che ci raggiungerebbe da una stella situata direttamente dietro il buco nero. È chiaro che le parole ordinarie qui fanno fatica a dare un senso a questa stranezza della fisica contemporanea: nulla è visibile ma tutto si osserva.

Esistono miriadi di problemi fisici che potrebbero essere descritti come inversi. Tra di loro, alcuni sono di natura a volte analitica, a volte geometrica. In questo articolo ci occupiamo di un problema molto specifico, di natura geometrica, le cui origini risalgono agli albori del XX secolo. con le opere di tre geofisici tedeschi. Ma prima di poterlo formulare, dobbiamo introdurre alcuni elementi del linguaggio della geometria riemanniana.

Chi non ha familiarità con questa branca della matematica, consideri questo esempio elementare. In estate, su una strada diritta esposta al sole, osserviamo spesso miraggi: quello che possiamo vedere in lontananza non è più l’asfalto, ma sono macchie di cielo che sembrano pozzanghere e che non raggiungeremo mai. 

La spiegazione è relativamente semplice: il calore rilasciato dall'asfalto devia i raggi di luce e li incurva vicino al suolo, il che ci fa vedere il cielo anziché la strada. Un primo modo per formulare questo problema è dire che l'indice di rifrazione della luce è stato modificato dalla temperatura. Secondo le leggi di Snell, questa modifica dell'indice, non omogenea (dipende dalla temperatura dell'aria che tende a riscaldarsi vicino all'asfalto), ma isotropa (non c’è una direzione preferenziale) porta ad una modifica della traiettoria della luce. Così gli scienziati spiegavano questo fenomeno nel diciassettesimo e diciottesimo secolo (e ancor oggi si insegna nelle scuole).

Con l'introduzione delle geometrie non euclidee nel XIX secolo, è apparso un modo nuovo di studiare questo problema. Invece di pensare che i raggi di luce si muovano curvando nel consueto spazio euclideo che abitiamo, è divenuto equivalente pensare che i raggi viaggino in linea retta in uno spazio intrinsecamente curvo. In questo modello, un fascio di luce sembra quindi muoversi in un mezzo la cui geometria potrebbe essere curva, come un aereo si sposta sulla superficie della Terra secondo un arco di cerchio. 

Naturalmente, tutta la difficoltà dell'impresa è di formulare ciò che questo "in linea retta" significa in termini matematici in uno spazio che non è più euclideo. Bisogna infatti ricorrere al concetto di geodetica. Una geodetica è la curva più breve che congiunge due punti di uno spazio. Lo spazio in questione può essere quello euclideo, una più generale varietà riemanniana (uno spazio “curvo”), o un ancor più generale spazio metrico in qualsiasi dimensione. Ad esempio, nel piano, le geodetiche sono le linee rette, su una sfera sono gli archi di cerchio massimo  Il termine generale con il quale si designano queste geometrie curve è quello di geometria riemanniana.

In termini matematici, diciamo che una modifica dell'indice di rifrazione corrisponde a una modifica della metrica dello spazio, che è all'origine della sua curvatura: la metrica, qui, è l'oggetto matematico che codifica la struttura dello spazio su scala infinitesimale. Darsi una metrica è, infatti, darsi un modo per misurare le distanze nello spazio che si vuole studiare: una sorta di regola la cui lunghezza potrebbe accorciarsi o aumentare in base alla nostra posizione e il nostro orientamento nello spazio. Facciamo un esempio semplice, parlando del problema del bagnino, un classico problema di ottimizzazione: un bagnino in spiaggia (chiamiamolo Bob) vuole salvare una persona che sta annegando (chiamiamola Alice). Nella metrica euclidea - che è quella che comunemente chiamiamo la distanza "a volo di uccello" - la distanza tra Bob e Alice è data dalla lunghezza della geodetica euclidea che li connette, cioè, il segmento rettilineo Bob-Alice. Ma Bob non si muove nella metrica euclidea, perché sa che corre più veloce di quanto faccia nuotando e quindi ha interesse a massimizzare il suo tempo di corsa a piedi e ridurre al minimo il tempo di nuoto per salvare Alice in tempo. Nella metrica di Bob, la geodetica che lo collega ad Alice non è più una linea retta - Bob non si muove più nella geometria euclidea, ma secondo una propria metrica.

I matematici designano generalmente una metrica con la lettera g; i fisici preferiscono la notazione ds². Ad esempio, in un piano con un determinato sistema di coordinate (Oxy), la metrica euclidea viene descritta come:

Si noti che questo è semplicemente il teorema di Pitagora. Ma altre metriche sono possibili, dando luogo ad altre geometrie (questa volta curve, e non più euclidee) in cui il teorema di Pitagora non è più valido o, meglio, è solo un caso particolare nel caso in cui sia valido il postulato delle parallele di Euclide.

Una delle più celebri geometrie non euclidee è la geometria iperbolica. Questa geometria in particolare descrive superfici come quella rappresentata in figura. Essa si ottiene tramite la metrica:

Le geodetiche sono in questo caso delle iperboli: la loro curvatura è negativa, perciò le geodetiche che partono dallo stesso punto con direzioni vicine (ma diverse) tenderanno a deviare molto rapidamente l'una dall'altra. Ciò che deve essere tenuto presente è il principio generale su cui poggia la geometria riemanniana: la curvatura dei raggi di luce viene interpretata come una curvatura intrinseca dello spazio in cui si muovono. Aggiungiamo incidentalmente che questo capovolgimento del punto di vista è stato cruciale nella storia della fisica in quanto ha consentito in particolare la formulazione matematica della teoria della relatività generale di Einstein all'inizio del XX secolo.

In seguito, ci concentreremo su uno dei casi le cui caratteristiche fisiche possono essere descritte a priori mediante geometrie non euclidee. I matematici pensano che il modo in cui la curvatura varia da luogo a luogo all'interno di una "varietà riemanniana" (il gergo matematico per indicare lo spazio curvo) determina i percorsi più brevi tra due punti qualsiasi. Interpretato nel linguaggio della geometria riemanniana, questo principio equivale a dire che le onde si muovono lungo le geodetiche della metrica.

Onde sismiche e interno della Terra - All'inizio del XX secolo, grazie al miglioramento tecnico dei sismografi, i geofisici hanno scoperto l'esistenza di due tipi di onde che si propagano nella crosta terrestre in seguito a un terremoto: le onde P e S. Le onde P (primarie), le cosiddette onde di compressione, sono le più veloci, si muovono a una velocità di 6 km/s vicino alla superficie della Terra e sono quindi le prime ad essere registrate dai sismografi. Nelle onde di compressione, l’impulso ha la stessa direzione della propagazione dell’onda, e si manifesta attraverso una serie di rarefazioni e compressioni del mezzo attraversato.

Poi giungono le onde S, dette onde trasversali o di taglio, più lente ma anche più devastanti per le costruzioni, perché tendono a spostare il mezzo perpendicolarmente alla direzione di propagazione dell'onda. Le onde S non si propagano nei fluidi.

Lo studio dei tempi di propagazione di queste onde nel corso del XX secolo ha portato a modelli sempre più raffinati della struttura interna della Terra, che è suddivisa in una crosta terrestre sottile, con uno spessore dell'ordine di poche decine di chilometri, un mantello, profondo fino a 3000 km, e infine un nucleo, una parte del quale è liquido e impedisce la propagazione delle onde S.

Dopo le prime scoperte sull'esistenza di queste onde, Herglotz, nel 1905, Wiechert e Zoeppritz, nel 1907, suggerirono un modello matematico per descrivere la struttura interna della Terra: quest'ultima è rappresentata da una sfera di raggio R ≃ 6300 km; la sua struttura è a simmetria sferica (cioè la sua densità dipende solo dalla distanza dal centro della Terra) ed è isotropica. In termini di geometria riemanniana, ciò equivale a supporre che la metrica che descrive la struttura interna della Terra sia proporzionale alla metrica euclidea di un fattore di proporzionalità 1/c², dove c descrive la velocità di propagazione delle onde P all'interno della Terra. Secondo le ipotesi precedenti, si presume che la funzione c sia radiale, vale a dire che dipende solo dalla distanza r dal centro della Terra.

Se indichiamo con g la metrica della Terra e g_eucl la metrica euclidea, allora:

Inoltre, affinché il modello fosse fedele all'osservazione, Herglotz e Wichert-Zoeppritz hanno ipotizzato che esso doveva soddisfare una condizione supplementare:

che traduce il fatto che la traiettoria delle onde è sempre più curva man mano che si avvicinano al centro della Terra. Da un punto di vista geometrico, se S_r designa una sfera di raggio r, e x e y sono due punti su questa sfera, allora l'unica geodetica che li collega è interamente contenuta all'interno della sfera. Infine, come già menzionato, si suppone che le onde sismiche di tipo P si propaghino secondo le geodetiche della metrica curvilinea g. 

Si supporrà anche che siano stati raccolti abbastanza dati sismici affinché, data qualsiasi coppia di punti x e y sulla superficie terrestre, il tempo di percorrenza di un'onda P da x (l'epicentro di un terremoto) a y (la stazione di registrazione) sia noto. 

Questo è un assunto molto forte che, in pratica, non è mai raggiunto a livello globale perché ci sarebbero troppe misure da eseguire, ma può esserlo almeno localmente, su una certa porzione del globo (ad esempio nelle vicinanze di faglie sismiche), o globalmente, estrapolando i risultati noti localmente. Si presume pertanto conosciuta la funzione di tale tempo di percorrenza (funzione distanza al bordo) (x, y) ↦ τ (x, y) che associa a qualsiasi coppia di punti (x, y) sulla superficie sferica il tempo di percorrenza stimato di un'onda da x a y. La domanda quindi è:

Se conosciamo il tempo di percorrenza dell’onda τ (x, y) da x a y per qualsiasi coppia di punti (x, y) sulla superficie della Terra, è possibile ricostruire la funzione della sua velocità c, vale a dire la metrica della Terra?

Questo problema pone in realtà due domande ausiliarie, che cerchiamo di descrivere. La prima è di ordine teorico: è teoricamente possibile ricostruire la funzione c di velocità delle onde? In altre parole, date due metriche sulla Terra, che scriviamo g e g', se supponiamo che i tempi di percorrenza associati alle due metriche coincidano, cioè che τ (x, y) = τ '(x, y) per qualsiasi coppia di punti (x, y) sulla superficie della Terra, è vero che c = c', cioè le funzioni di velocità dell'onda sono le stesse? In termini matematici, questo è chiamato un problema di iniettività. Se possiamo rispondere positivamente a questa domanda, diremo che la funzione del tempo di propagazione determina la metrica della Terra.

In realtà è possibile considerare una classe di metriche un po’ più generale di quelle fin qui citate. Ad esempio, possiamo immaginare che la funzione c non dipenda solo dalla distanza dal centro della Terra, ma anche da altri parametri posizionali. Ancor più difficile è la seconda domanda: è possibile immaginare che la metrica non sia isotropa, cioè che siano preferite certe direzioni di propagazione delle onde sismiche? In pratica, ciò dipende dal tipo di materiale attraversato dall'onda: l'olivina, ad esempio, che costituisce gran parte del mantello terrestre, è un minerale altamente polarizzato; a seconda del suo orientamento, il rapporto delle velocità di propagazione delle onde può variare fino al 25%. Questa forte anisotropia si deve dunque ritrovare alla scala della metrica.

In ogni caso, supporremo almeno che la metrica terrestre g sia semplice, vale a dire che ogni coppia di punti (x, y) del globo è legata da una singola geodetica. Da un punto di vista fisico, ciò significa che un'onda sismica che parte da x e arriva a y ha seguito un singolo percorso: non si è divisa in due prima di essere ricomposta in y. Ancora, le osservazioni sismiche mostrano che questa ipotesi non è del tutto esatta. Ma non farlo complicherebbe seriamente il problema (e, anche, lo renderebbe insolubile).

Nel 1981 che il matematico francese René Michel pubblicò un articolo nella rivista Inventiones Mathematicae, in cui affermava la seguente congettura, che ora porta il suo nome:

Congettura di Michel (1981): se la metrica è semplice, essa è determinata dalla funzione del tempo di percorrenza.

In altre parole, la congettura di Michel afferma che la conoscenza della funzione del tempo di propagazione τ delle onde sismiche è teoricamente sufficiente per conoscere la metrica g. Assai presto i matematici capirono che il problema di Michel era difficile e, tranne alcuni casi molto particolari, pochi risultati arrivarono a sostenere la congettura. Ci sono voluti più di venti anni perché fosse risolta in due dimensioni da Leonid Pestov e Gunther Uhlmann, in un articolo sul giornale americano Annals of Mathematics. La loro dimostrazione va ben oltre il nostro scopo, ma ci accontenteremo di fare due osservazioni al riguardo. Da un lato, la loro dimostrazione non ha permesso di dimostrare la congettura nella dimensione 3 (o anche in dimensione più grande), che è proprio il caso che ci interessa, poiché il pianeta Terra è una "palla" tridimensionale. Inoltre, non è stata costruttiva, cioè ha risposto positivamente alla congettura di Michel affermando che è teoricamente possibile ricostruire la metrica, ma non ha detto come farlo.

Infatti, non solo è necessario sapere che la ricostruzione è possibile, ma è anche necessario dare una formula o un algoritmo che permetta il calcolo pratico della metrica g. Questo problema, chiamato congettura di rigidità di contorno, è stato affrontato nel 2017 dai tre matematici Plamen Stefanov (Purdue University di West Lafayette, Indiana), Gunther Uhlmann (Università di Washington, Seattle) e Andras Vasy (Stanford University, California) in uno studio, presentato all'University College di Londra (UCL), che utilizza le più moderne tecniche di analisi che si definiscono come analisi microlocali. La congettura afferma che conoscere le lunghezze dei cammini più brevi tra i punti di un contorno determina essenzialmente la curvatura totale (Si dice quindi che la geometria sia "rigida"). Quindi, misurando il modo in cui le onde viaggiano all'interno di uno spazio curvo, si potrebbero elaborare i percorsi più brevi e, teoricamente, la struttura generale.

Nello specifico, i tre matematici hanno considerato l’ipotesi, che differisce da quella di Michel, che lo spazio curvo sia strutturato in strati concentrici. Ciò ha permesso loro di costruire una soluzione in più fasi. "Strato dopo strato, come sbucciare una cipolla", ha detto Uhlmann, in modo da ricostruire la metrica grazie ad un determinato algoritmo. 

La loro idea è di risolvere il problema prima localmente, ricostruendo la metrica in prossimità della superficie terrestre grazie a una relazione relativamente esplicita che utilizza solo il tempo di viaggio delle onde che restano vicino alla superficie terrestre. Quindi, sfruttando la laminazione convessa (o "peeling"), mostrano che si può “scavare” sempre di più nella Terra, vale a dire applicare nuovamente il loro metodo di ricostruzione locale su uno strato leggermente più profondo. E così via, passo dopo passo, il loro algoritmo consente la ricostruzione della metrica fino a raggiungere il centro della Terra. La pubblicazione del loro studio ha anche dato origine a un articolo su Nature, che è un fatto abbastanza raro riguardo a un risultato matematico e quindi va sottolineato.

Attualmente, la ricerca è incentrata sull'implementazione numerica del metodo Stefanov-Uhlmann-Vasy. Per esso è certamente interessante avere un algoritmo che inverte la funzione di tempo di percorrenza e ricostruisce la metrica, ma è ancora necessario codificarlo con il computer, per confrontarlo con una mole maggiore di dati reali, vale a dire senza fare troppi errori di arrotondamento. Questo non è un compito facile. Un primo tentativo, datato 2018 e considerando un quadro un po' semplificato, sembrerebbe confermare che questo approccio è legittimo. Caso da seguire, quindi, in quanto non sappiamo ancora se le metriche semplici verifichino il requisito di laminazione convessa richiesto per il funzionamento dell'algoritmo Stefanov-Uhlmann-Vasy. È probabile che sia così, ma i matematici sono in attesa di ulteriori verifiche. 

Applicare la teoria a reali dati geofisici non avverrà immediatamente, come sostiene Maarten de Hoop, un sismologo computazionale della Rice University di Houston, in Texas. Una difficoltà è che la teoria presuppone che ci siano informazioni in ogni punto. In realtà, i dati sono raccolti solo in località relativamente sparse. Uhlmann dice che sta lavorando su quel problema con colleghi specializzati in analisi numerica.

La congettura di Michel è quindi sospesa su quest'ultimo aspetto. Da laureato in geologia, non posso nascondere alcune mie perplessità di fondo: l’interno della Terra è a mio parere difficilmente assimilabile a una varietà riemanniana a simmetria sferica. Esso non è isotropo, presenta discontinuità importanti, come quella Mohorovičić, scoperte proprio grazie alle onde sismiche, che segnano un cambiamento di composizione delle rocce, e altre, che segnano un cambiamento del loro stato fisico (nell'astenosfera del mantello superiore le rocce sono in uno stato semifluido, il che significa anche che si muovono, come magmi o come corpi plastici per reomorfismo, in contrasto con l’assunto della rigidità). Anche il mantello esterno presenta rocce allo stato fluido, in corrispondenza di un brusco cambiamento di densità rispetto al mantello interno. È probabile che Stefanov, Uhlmann e Vasy sappiano apportare le dovute correzioni al loro modello per tener conto di queste diverse condizioni, ma la dimostrazione della congettura di Michel perderebbe uno dei suoi auspicati vantaggi: l’applicabilità ad altri campi oltre a quello geofisico senza dover ricominciare tutto daccapo.

Riferimenti: 

Thibault Lefeuvré — « Le chant de la Terre » — Images des Mathématiques,CNRS, 2018