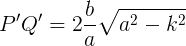Sinisgalli e la poesia come numero complesso

In tutta la sua opera, Leonardo Sinisgalli evidenzia la potenza conoscitiva della matematica, della geometria, e delle scienze in genere. Tuttavia, poiché la «verità» è sempre più sfuggente, «sottile», la sola indagine scientifica non basta: a un certo punto è indispensabile uno scatto, una «folgorazione improvvisa». Dovrà essere il poeta a tentare di cogliere frammenti di verità e consegnarli agli uomini. Il calcolo infinitesimale, presupposto delle nuove geometrie algebriche, ha spianato la strada verso la descrizione della realtà nella sua più minuta e ondivaga essenza, indeterminabile ma non per questo inesprimibile. In una lettera indirizzata all'amico Gianfranco Contini, spesso citata dai critici, Sinisgalli sostiene, con una metafora provocatoria ed efficace, che la funzione della poesia, che appartiene per sua natura alla sfera dell’imponderabile, può essere espressa come

"un quantum, una forza, un’estrema animazione esprimibile mediante un numero complesso a + bj […] dove a e b sono quantità reali, e j è il famoso operatore immaginario. Questo operatore dà un senso, un’inclinazione al numero che, per sua natura, è orizzontale e inerte, lo rende attivo, lo traduce in una forza. A me pare analoga l’azione di j a quella che il poeta esercita sulla «cosa». Le parole per formare un verso devono avere una particolare inclinazione […]. Voglio dire, insomma, che il simbolo j ci darebbe un’idea di quella che è l’alterazione provocata dal linguaggio sulla realtà, del rapporto, cioè, tra «cosa» e «immagine». La poesia in ultimo non è un fenomeno naturale, si sottrae costituzionalmente alla voragine entropica dell’universo, è piuttosto evento sintropico, irripetibile, caratterizzato da un’intrinseca “misteriosa finalità”.”

Questa inclinazione fornita da j ricorda il clinamen lucreziano, l’impercettibile ma fondamentale deviazione dalla verticale nella caduta inerte degli atomi, grazie al quale la materia si organizza in un senso e dalle particelle infinitesimali si passa alle cose. Allo stesso modo, la parola poetica acquista direzione vettoriale rispetto al flusso puramente rettilineo e referenziale del linguaggio, agendo sulla cosa descritta in senso straniante. In questa considerazione riemerge la passione di Sinisgalli per i numeri immaginari (il numero complesso è formato da una parte reale e una immaginaria). Questo prodigio concettuale, che compare e assume dignità matematica con gli algebristi italiani del Rinascimento, diventerà, nella matematica moderna, un vettore, cioè una direzione, un’inclinazione. Inoltre, i numeri immaginari e quelli complessi, il calcolo matriciale e i quaternioni possono ora dare conto di una realtà pluridimensionale, con i suoi movimenti, le tensioni, le torsioni, gli spin. 

Il numero immaginario con cui viene definita la specificità poetica corrisponde, al di là di metafora, a un’istanza comunque razionale, a un’entità calcolabile. Per Sinisgalli l’attività poetica è allo stesso tempo misura, regola e «ispirazione» che dà «bagliore metafisico» e che declina in perturbazione fisiologica, in metabolismo, seguendone gli esiti di uno sviluppo storico che vede la poesia andare «verso la prosa». La poesia diventa forma del respiro del poeta, e non più traduzione dell’ideale, dell’assoluto, come voleva definirla Croce. Così tutto ciò che avvicina la poesia a una formula algebrica, perde di peso ed è preda di una crisi metrica. Lo sguardo del poeta non è più euclideo. Oggi la poesia ha contorni più «rotti», e «la sua forma, per via della sua volubilità, della sua indeterminatezza, si avvicina a una forma vivente», immagine organica del sistema che prolifera e cresce per margini, in modo frattale, o senza direzioni predefinite e preferenziali, in modo rizomatico, e non si offre più con la geometria algida di un cristallo.

Gli indivisibili di Cavalieri

Jorge Luis Borges, ossessionato dall’idea di infinito, nella terza nota a La Biblioteca di Babele, in Finzioni (1944), fa questa considerazione, attribuendola come suo solito a un autore inventato:

“Letizia Alvarez de Toledo ha osservato che la vasta Biblioteca è inutile; a rigore, basterebbe un solo volume, di formato comune, stampato in corpo nove o in corpo dieci, e composto d'un numero infinito di fogli infinitamente sottili. (Cavalieri, al principio del secolo XVII, affermò che ogni corpo solido è la sovrapposizione d'un numero infinito di piani). Il maneggio di questo serico vademecum non sarebbe comodo: ogni foglio apparente si sdoppierebbe in altri simili; l'inconcepibile foglio centrale non avrebbe rovescio”. 

 Il riferimento dello scrittore argentino è al cosiddetto Principio di Cavalieri, anticipato dalle idee di Oresme, Keplero e Galileo ed espresso dal matematico milanese Bonaventura Cavalieri, che afferma che un’area può essere considerata come formata da un numero indefinito di segmenti paralleli equidistanti e sottilissimi (“indivisibili”) e che allo stesso modo un volume può essere considerato come composto da un numero indefinito di aree piane parallele. Cavalieri si rese conto che il numero di indivisibili che costituiscono un’area o un volume deve essere indefinitamente grande, tuttavia non cercò di approfondire questo fatto (che, come vedremo, gli costò feroci critiche), limitandosi a una serie di suggestive metafore: una retta è composta da punti come un rosario da grani; una superficie è composta da rette come una stoffa da fili e un volume è composto da aree piane come un libro da pagine. 

Ma chi era Cavalieri? Nato a Milano nel 1598 e battezzato Francesco, Cavalieri assunse il nome del padre, Bonaventura, quando nel 1615 entrò nei Gesuati, un ordine secolare che sarebbe stato soppresso nel 1668 da Clemente IX sia per carenza di vocazioni, sia perché i suoi beni servivano per pagare i Veneziani nella guerra contro i Turchi. Cavalieri studiò teologia nel convento di San Gerolamo a Milano e poi geometria all’Università di Pisa, dove fu allievo di padre Benedetto Castelli, collaboratore di Galileo, che si accorse della sua forte inclinazione per la matematica.

Terminati gli studi, nel 1619 si candidò alla cattedra di matematica a Bologna, ma fu considerato troppo giovane per l’incarico. Analoghi rifiuti gli giunsero da diversi altri atenei, tra i quali quelli di Pisa e di Roma, al punto che si chiedeva se non ci fosse una prevenzione nei suoi confronti a causa dell’appartenenza ai Gesuati, congregazione molto chiacchierata e malvista dalle gerarchie romane. Nel 1621 conobbe Galileo, del quale volle subito dichiararsi allievo. L’incontro era stato propiziato da Federico Borromeo (il cardinal Federigo di manzoniana memoria), che conosceva e stimava Cavalieri al punto da farlo diacono e suo assistente. Iniziò allora una lunga corrispondenza con lo scienziato pisano, durata per circa vent’anni. Fu in questo periodo che ideò il metodo degli indivisibili per il calcolo di aree e volumi, al quale è associato il suo nome, che anticipa il calcolo integrale e ricorda il metodo di esaustione degli antichi. In una lettera del 1621 a Galileo scriveva:

“Vado dimostrando alcune proposizioni d'Archimede diversamente da lui, et in particolare la quadratura della parabola, divers’ancora da quello di V.S.” 

Galileo lo incoraggiò a pubblicare in un libro le sue idee, dichiaratamente influenzate da Keplero, che, nella Stereometria doliorum vinariorum (1615) aveva calcolato aree e volumi suddividendo i corpi in infinite parti infinitesime, giungendo a risolvere il problema della quadratura dell’ellisse. Cavalieri sviluppò il suo metodo negli anni successivi. Nel novembre del 1627, in un’altra lettera a Galileo, sosteneva di essere in procinto di pubblicare un libro sull’argomento, 

“ho perfettionato un'opera di geometria…. Et è cosa nova, non solo quanto alle cose trovate, ma anco al modo di trovarle, da niuno adoperate insin'ora, ch'io mi sappi”. 

Finalmente ottenuta nel 1629 la sospirata cattedra di matematica a Bologna, ritardò la pubblicazione della sua opera a causa di ripensamenti e riscritture, ma soprattutto per rispetto verso Galileo, che Cavalieri pensava dovesse pubblicare un’opera sugli infinitesimi. In realtà il pisano era interessato solo al risvolto fisico del problema, la struttura atomica della materia, e non intendeva approfondire l’aspetto matematico. Finalmente, nel 1635, diede alle stampe Geometria Indivisibilibus Continuorum Nova Quadam Ratione Promota (Un certo metodo per lo sviluppo di una nuova geometria dei continui indivisibili). Nel testo Cavalieri parla a proposito delle superfici come formate dalla “totalità di tutte le linee” e dei solidi come formati dalla “totalità di tutti i piani”, ciò gli consente di introdurre il suo principio, con il quale giunge a elaborare un nuovo strumento per la determinazione di aree e volumi. Nella sua prima è più semplice formulazione, il principio afferma che: 

“se due solidi hanno uguale altezza e se le sezioni tagliate da piani paralleli e ugualmente distanti da queste stanno sempre in un dato rapporto, anche i volumi dei solidi stanno in questo rapporto”.

Leggiamo dalle sue stesse parole, tratte dalla Geometria Indivisibilibus, come egli sia giunto alla formulazione di tale principio. Così scrive nelle pagine introduttive: 

“Meditando dunque un giorno sulla generazione dei solidi che sono originati da una rivoluzione intorno ad un asse e confrontando il rapporto delle figure piane generatrici con quello dei solidi generati mi meravigliavo moltissimo del fatto che le figure generate si discostassero a tal punto dalla condizione dei propri genitori da mostrare di seguire un rapporto completamente diverso dal loro. Per esempio un cilindro, che sia ottenuto insieme ad un cono della stessa base per rotazione attorno a un medesimo asse, è il triplo di esso, anche se nasce per rivoluzione da un parallelogramma doppio del triangolo che genera il cono. [...] 

Avendo dunque più e più volte fermato l'attenzione su tale diversità in moltissime altre figure, mentre prima, raffigurandomi ad esempio un cilindro come l'unione di parallelogrammi indefiniti per numero e il cono con stessa base e stessa altezza come l'unione di triangoli indefiniti per numero passanti tutti per l'asse, ritenevo che ottenuto il mutuo rapporto di dette figure piane dovesse subito venirne fuori anche il rapporto dei solidi da esse generate, risultando invece già chiaramente che il rapporto delle figure piane generatrici non concordava affatto con quello dei solidi generati mi sembrava si dovesse a buon diritto concludere che avrebbe perduto il tempo e la fatica e che avrebbe trebbiato inutile paglia chi si fosse messo a ricercare la misura delle figure con tale metodo. Ma dopo aver considerato la cosa un po' più profondamente pervenni finalmente a questa opinione e precisamente che per la nostra faccenda dovessero prendersi piani non intersecantisi tra di loro, ma paralleli. In questo infatti, investigati moltissimi casi, in tutti trovai perfetta corrispondenza tanto tra il rapporto dei corpi e quello delle loro sezioni piane quanto tra il rapporto dei piani e quello delle loro linee [...]. 

Avendo dunque considerato il cilindro e il cono suddetti secati non più per l'asse ma parallelamente alla base, trovai che hanno rapporto uguale a quello del cilindro al cono quei piani che chiamo nel libro II ``tutti i piani'' del cilindro a ``tutti i piani'' del cono, con riferimento alla base comune [...]. Stimai perciò metodo ottimo per investigare la misura delle figure quello di indagare i rapporti delle linee al posto di quello dei piani e i rapporti dei piani al posto di quello dei solidi per procurarmi subito la misura delle figure stesse. La cosa, ritengo, andò come era nei miei voti, come risulterà chiaro a chi leggerà tutto”. 

Nei primi due libri dell’opera, Cavalieri espone le ”proposizioni lemmatiche” sulle quali si basa il suo metodo, introduce il concetto di “tutte le linee” di una figura piana e di “tutti i piani” di una figura solida e stabilisce che “tutte le linee” di figure piane (e “tutti i piani di figure solide”) sono grandezze che hanno tra loro rapporto, per cui è possibile poter operare con esse. Ai lemmi si aggiungono poi dimostrazioni e corollari riguardanti, rispettivamente, le sezioni cilindriche e coniche (Libro I) e i triangoli, i parallelogrammi e i rettangoli e le figure le solide derivanti dalle loro rotazioni di (Libro II). 

Il Libro III è dedicato al cerchio, all’ellisse e ai solidi da essi generati. Come esempio del metodo degli indivisibili, vediamo come Cavalieri determina l’area racchiusa dall’ellisse. 

Consideriamo un ellisse di asse maggiore 2a ed asse minore 2b e un cerchio che ha come diametro l'asse maggiore dell'ellisse. Ogni retta perpendicolare al diametro intercetta sul cerchio il segmento PQ e sull’ellisse il segmento P’Q’ considerati appunto come indivisibili delle due curve. Il rapporto fra i due segmenti è a/b. 

Infatti, utilizzando il linguaggio della geometria analitica le equazioni delle curve sono: 

 

Intersecando le due coniche con rette parallele all’asse delle ordinate, di equazione x = k, si ottengono le coordinate e quindi le misure dei due segmenti intercettati: 

il cui rapporto è sempre a/b. 

Per il principio di Cavalieri, allora, un uguale rapporto deve intercedere fra l'area del cerchio e quella dell'ellisse in quanto il cerchio è la totalità delle linee PQ e l’ellisse la totalità delle linee P’Q’. Indicando con A l'area dell'ellisse avremo: 

quindi: 

Nei libri successivi Cavalieri dimostra i risultati relativi a figure piane e solide originate dalle sezioni coniche e dalle spirali. Nel libro VII, l’ultimo, formula quello che chiamerà “secondo metodo” in cui chiarisce i fondamenti degli indivisibili. Nel teorema I espone la versione definitiva di quello che ancor oggi è noto come "principio di Cavalieri": 

"Figure piane qualsiasi, poste tra le stesse parallele, in cui, condotte linee rette qualunque equidistanti alle parallele in questione, le porzioni così intercettate di una qualsiasi di queste rette siano uguali, sono parimenti uguali tra loro. E figure solide qualsiasi, poste tra gli stessi piani paralleli, in cui, condotti piani qualunque equidistanti a quei piani paralleli, le figure piane di uno qualsiasi dei piani condotti così determinate nei solidi siano uguali, saranno parimenti uguali tra loro. Si chiamino allora tali figure ugualmente analoghe, sia le piane che le solide confrontate tra loro, e rispetto alle linee di riferimento, o i piani paralleli, tra i quali si suppongono poste, se è necessario indicarlo". 

 Questo principio si dimostra facilmente “a posteriori” con gli strumenti del calcolo integrale, perchè equivale a dire che due integrali definiti, tra gli stessi estremi di integrazione, aventi uguali funzioni integrande, sono uguali; o che se due funzioni hanno rapporto costante allora i loro integrali definiti hanno lo stesso rapporto (una costante moltiplicativa si può portare indifferentemente dentro o fuori dal segno di integrazione): se f(x) = kg(x) allora: 

Cavalieri applica il principio per calcolare aree e volumi confrontando le proprietà di due figure (ad esempio le aree di due superfici o i volumi di due solidi) sulla base del rapporto fra gli indivisibili staccati dall'una e dall'altra sopra un medesimo fascio di rette parallele o di piani paralleli. Il metodo gli consente, ad esempio, di verificare la validità di alcuni problemi risolti da Archimede con il metodo di esaustione sul calcolo dei volumi dei solidi (come il volume del cono è 1/3 di quello del cilindro con la stessa base e la stessa altezza). Allo stesso modo tratta l’area compresa fra due curve, considerando le aree come somma delle ordinate, e se le ordinate stanno in un certo rapporto allora anche le aree stanno nello stesso rapporto. 

Cavalieri conosce il metodo di esaustione, ma è convinto della superiorità del metodo degli indivisibili rispetto ad esso: l’esaustione fa uso essenzialmente della dimostrazione per assurdo, mentre il metodo degli indivisibili è un metodo costruttivo per calcolare aree e volumi. 

Un importante risultato ottenuto da Cavalieri, presentato nell’opera Centuria di varii problemi (1639), riguarda l’area sottesa a certe curve algebriche. Nella moderna simbologia dell’analisi, esso corrisponde alla formula: 

che Cavalieri dimostrò per i valori interi di n compresi tra 1 e 9. La dimostrazione è puramente geometrica. Utilizzando metodi algebrici, Newton generalizzerà la formula, estendendola a tutti i valori razionali di n. 

L’opera di Cavalieri non venne accolta con molto favore dai geometri sostenitori del pensiero e dell’opera di Archimede. In particolare dovette subire le critiche del matematico svizzero Paul Guldin, noto come Guldino, un ebreo convertito poi diventato gesuita, che era stato solidale con padre Orazio Grassi nella polemica contro Galileo sulle comete e arrivò persino ad accusare Cavalieri di plagio nei confronti di Keplero. Come tutti i gesuiti, Guldino si impegnò a screditare i fondamenti della teoria degli infinitesimi, attaccando Cavalieri nel libro De centro gravitatis, trium specierum quantitatis continuæ, pubblicato a Vienna tra il 1635 e il 1641. L’obiezione principale riguardava la natura delle grandezze geometriche continue (linee, superfici, solidi), a proposito delle quali Guldino sostiene l'impossibilità che vengano costruite riunendo grandezze aventi una dimensione in meno:

"che dunque quella superficie sia, e in linguaggio geometrico possa chiamarsi tutte le linee di tale figura, ciò a mio avviso non gli sarà concesso da nessun geometra; mai infatti possono essere chiamate superficie più linee, oppure tutte le linee; giacché la moltitudine delle linee, per quanto grandissima essa sia, non può comporre neppure la più piccola superficie.” 

La tesi di Guldino è che “il continuo è divisibile all'infinito, ma non consta di infinite parti in atto, bensì soltanto in potenza, le quali [parti] non possono mai essere esaurite”. La conclusione di Guldino è che “questa proposizione sulle figure piane non è stata in alcun modo dimostrata in maniera valida”. Il bersaglio delle critiche dei geometri gesuiti è proprio il concetto di vicinanza infinita, che sfugge ad ogni tentativo di definizione geometrica rigorosa (e soprattutto va in direzione contraria al metodo di Esaustione di Archimede). 

In risposta alle critiche, Cavalieri, nel 1647, pubblicò Contro Guldino. Esercitazione terza, inclusa nelle Exercitationes geometricae sex. Così Cavalieri critica alcune contestazioni di Guldino: 

“Infatti in molti passi, sia Archimede, sia molti altri dediti alla Geometria più pura, dimostrano che si possono inscrivere, e circoscrivere ad una figura data altre figure, in modo che la figura circoscritta superi l’inscritta per una grandezza, la quale sia minore di qualsiasi grandezza data del medesimo genere. Concludono dunque che la circoscritta è uguale all’inscritta? Per niente affatto; adoperato invece un altro termine medio, dimostrano che la figura alla quale è stata fatta l’inscrizione e la circoscrizione, è uguale a una certa altra, la quale sia invero minore della circoscritta, maggiore invece della inscritta”. 

La polemica finì per concentrarsi su questioni filosofiche: il metodo di esaustione sostenuto da Guldino è rigoroso, ma scomodo, mentre quello degli indivisibili è di più immediata applicazione pratica, anche se non è ancora sorretto da un adeguato impianto concettuale e formale. Polemicamente, Cavalieri giunse ad affermare persino che “il rigore (...) è affare della filosofia e non della geometria”. 

Nelle già citate Exercitationes geometricae sex del 1647, Cavalieri, seguendo una via diversa, confrontò non più singoli indivisibili corrispondenti sulle due figure, ma la somma degli indivisibili della prima figura con la somma di quelli della seconda. La teoria degli indivisibili può essere applicata per dimostrare, ad esempio, che l’area di un parallelogramma è il doppio dell’area di ognuno dei triangoli in cui lo suddivide ciascuna delle diagonali. 

Se, nel parallelogramma ABCD si scelgono, sui lati AD e BC, i punti G ed E in modo che GD = BE, allora i segmenti GH ed FE della figura, aventi il secondo estremo sulla diagonale, e paralleli alla base, hanno la stessa lunghezza. Quindi i due triangoli ABD e BCD sono composti da due somme uguali di segmenti a uno a uno corrispondenti, e quindi, secondo il principio degli indivisibili, le loro aree sono uguali. 

Nonostante le critiche, il metodo degli indivisibili si diffuse subito in Italia e in Europa.. Non mancarono ulteriori sviluppi, soprattutto grazie a Torricelli, che con il metodo di Cavalieri riuscì a calcolare il volume del solido iperbolico, suscitando l’ammirazione dei contemporanei e il loro stupore, dato che il problema era ritenuto impossibile. Torricelli ebbe l’accortezza di accostare alla dimostrazione con il metodo degli indivisibili anche quella “con il metodo solito di dimostrazione degli antichi geometri, il quale è bensì più lungo ma non per questo, secondo me, più sicuro”. 

Lo stesso Torricelli non mancò tuttavia di esprimere perplessità sul metodo di Cavalieri invitando alla prudenza nel suo impiego. In molti frammenti, raccolti sotto il titolo di Contro gl’infiniti, Torricelli presenta diversi ragionamenti fallaci, tranelli in cui si può facilmente cadere facendosi prendere troppo dal fascino degli indivisibili. Torricelli mostra ad esempio una variante scorretta del ragionamento sul parallelogramma,, che conduce ad un risultato erroneo. 

Il triangolo ABD è unione dei segmenti, paralleli ad AD, delimitati dal lato AB e dalla diagonale BD: FG è uno di questi. Analogamente, il triangolo BDC è formato dai segmenti che, come FE, sono paralleli ad AB e sono delimitati dal lato BC e dalla diagonale. Confrontando a due a due i segmenti delle due schiere, come FG e FE, si vede che ad ogni segmento del triangolo ABD ne corrisponde, nel triangolo BDC, uno più lungo. Apparentemente segue che l’area di BDC è maggiore di quella di ABD, il che, naturalmente, è falso. 

Cavalieri ebbe il merito di aver coraggiosamente preso in esame il concetto di infinitesimo e per questo deve essere considerato come uno degli anticipatori del Calculus. Il suo metodo sembrava destinato a un impiego duraturo, tuttavia, ben presto ritenuto laborioso e non sufficientemente rigoroso, venne abbandonato in seguito alla diffusione di nuovi e potenti strumenti di calcolo.

L’Analytical Society contro il “rimbambimento” della matematica inglese

Dopo Newton, la ricerca matematica inglese andò incontro a una lunga crisi, dalla quale tentò di risollevarla Robert Woodhouse (1773-1827), fautore di un rinnovamento dell’algebra attraverso lo strumento del calcolo, che i professori dei college vedevano come “una pericolosa innovazione” in grado di minare “l’onore nazionale”. 

La matematica britannica era all’epoca solamente un mezzo per comprendere i Principia di Newton, che erano visti come la pietra di volta della conoscenza umana sia di Dio che del mondo naturale. La moderna analisi algebrica francese era vista da molti come il simbolo dei recenti rivolgimenti politici sul continente: era l’orribile risultato dell’intelletto umano lasciato libero da tutti i vincoli sociali. La natura astratta di una pura analisi algebrica permetteva in apparenza alle mente di vagare nella fantasia attraverso l’insensata manipolazione di simboli. Essa era inoltre collegata a una visione meccanica della mente. La matematica pura non era pertanto vista come una parte appropriata dell’educazione di Cambridge. Al contrario, tutti i libri di testo e i manuali erano dipendenti da figure geometriche e si applicavano a specifiche fondamenta fisiche. 

I Principles of analytical calculation (1803) di Woodhouse, che proponeva di sostituire la notazione di Newton a puntini con quella dei differenziali leibniziani, sollevarono scandalo, ma trovarono attenti lettori in un gruppo di giovani studenti di Cambridge, tra i quali Charles Babbage (1792-1871) e J. William Herschel (1792-1871). Essi erano ammirati dalle più potenti tecniche di calcolo dell’analisi matematica continentale e volevano collegarsi a “un secolo di progresso straniero” nel calcolo. I loro ispiratori erano filosofi naturali e matematici come Pierre-Simon Laplace, Joseph Louis Lagrange e Sylvestre Lacroix, i cui testi e manuali erano allora all’avanguardia. 

Babbage e Herschel si procurarono, nonostante la guerra in corso, una copia del Traité élémentaire de calcul différentiel et intégral (1802) di Lacroix (secondo Babbage “so perfect that any comment was unnecessary”) e diedero vita a una Analytical Society, con lo scopo di realizzare l’eretico progetto verso la memoria di Newton di tradurre il testo del francese e introdurre il calcolo e la notazione leibniziani. Il 1813 vide il primo frutto di questi “giovani infedeli”, un volume di Memoirs of the Analytical Society, che Babbage, dal carattere già allora piuttosto insofferente verso le istituzioni, avrebbe voluto irriverentemente intitolare “I principi del puro d-ism in opposizione alla dot-age dell’Università”. D-ism indicava ovviamente la d dei differenziali (ma richiamava anche deism), mentre dot-age indicava l’era dei punti di Newton, ma in inglese dotage significa “rimbambimento”!

La traduzione del libro di Lacroix fu completata nel 1816 da Babbage, Herschel e George Peacock (1791-1858). L’establishment di Cambridge fu enormemente scosso quando Peacock, diventato nel frattempo esaminatore all’Università, utilizzò la notazione differenziale nei testi per gli esami di calcolo del 1817. L’Analytical society produsse poi alcuni quaderni di esercizi e, nel 1820, oramai vittoriosa, si sciolse. Herschel avrebbe continuato gli studi astronomici del padre, mentre Babbage si sarebbe poi dedicato alla meccanizzazione del calcolo, ma questa è un’altra, meravigliosa, storia.

John Wallis, antipatico e geniale

Di carattere scontroso e indisponente, il matematico inglese John Wallis (1616-1703) non perdeva occasione per fare polemica. Famosa fu la sua disputa ventennale a suon di velenosi pamphlet con Thomas Hobbes (l’autore del Leviatano) sulla pretesa di quest’ultimo di aver realizzato la quadratura della circonferenza e sugli attacchi che il filosofo aveva mosso contro la nuova filosofia sperimentale. La contesa, iniziata nel 1655, si interruppe solo con la morte di Hobbes nel 1679. Un’altra controversia lo vide contestare all’ecclesiastico William Holder la priorità dell’invenzione di un metodo per insegnare a parlare ai sordomuti. Non contento, ebbe anche il tempo di manifestare tutto il suo spirito nazionalistico contestando (non del tutto a torto) a Cartesio di aver copiato l’algebra di Thomas Harriot.

Anche in politica, nei tempi tempestosi della rivoluzione di Cromwell e della successiva restaurazione monarchica, molti non apprezzarono affatto il suo saper navigare al servizio prima di uno e poi dell’altro dei contendenti. Non desta pertanto sorpresa che non fosse amato da molti contemporanei, tra i quali il bizzarro biografo John Aubrey, che lo accusò di essere plagiario delle idee di altri, “togliendo loro le piume per adornare il proprio cappello”. Eppure la sua grandezza scientifica è incontestabile, se lo stesso Isaac Newton, che non era prodigo di complimenti per i suoi colleghi, lo considerava tra i più grandi matematici del Seicento. 

Sebbene avesse ricevuto un’educazione umanistica eccellente (tra l’altro aveva imparato il latino, il greco e l’ebraico), Wallis, figlio di un pastore anglicano del Kent, era in gioventù completamente digiuno di matematica, che conobbe quasi casualmente grazie a un libro di aritmetica prestatogli dal fratello maggiore. Come scrisse egli stesso nella sua autobiografia: 

“Proseguii [con la matematica] come un piacevole passatempo nelle ore libere, se mi capitavano tra le mani libri di aritmetica o di altri argomenti matematici, senza che nessuno mi dicesse quali leggere, quali cercare, o con quale metodo procedere. Infatti la matematica non era a quei tempi considerata parte dell’educazione accademica, ma piuttosto un affare di commercianti, mercanti, marinai, falegnami, geometri o gente simile (…)”.

Wallis era destinato alla carriera ecclesiastica, e si diplomò Master of Arts in teologia e morale nel 1640, poco dopo aver ricevuto gli ordini. Per qualche tempo servì qua e là come cappellano privato, finché, nel 1643, la ricca eredità materna gli consentì di affrancarsi dal bisogno di lavorare per mantenersi: diventò un uomo agiato. 

Nel paese, la ribellione del Parlamento contro le pretese assolutistiche di Carlo I era intanto sfociata in guerra aperta, e Wallis prese le parti dei ribelli. Nel 1642, durante una cena, gli furono mostrati alcuni messaggi cifrati delle forze realiste, che egli fu in grado di decifrare in poco tempo. Il suo talento fu presto sfruttato dalla intelligence di Cromwell durante la lunga guerra civile: Wallis ebbe un ruolo importante nella capacità delle forze parlamentari di conoscere in anticipo le manovre degli avversari. La sua opera è stata paragonata a quella del gruppo di Turing a Bletchey Park, che svelò il mistero di Enigma, il sistema di comunicazione in codice dei tedeschi. 

La qualità della crittografia era all’epoca assai eterogenea: si usavano infatti sia banali sistemi basati sulla trasposizioni di lettere (che Wallis riconobbe e interpretò già durante la cena stessa di cui abbiamo parlato), sia algoritmi combinatori di lettere, cifre e altri simboli, sia i più evoluti metodi a chiave variabile. Wallis si rese conto che gli ultimi (“inventati dai francesi”) erano più sicuri, al punto da giudicarli “inattaccabili”, ma probabilmente la sua affermazione serviva a scoraggiare eventuali richieste di rivelare le proprie conoscenze (nel 1697 avrebbe rifiutato la richiesta di Leibniz di insegnare la crittografia agli studenti di Hannover).

Continuava intanto la sua formazione matematica da autodidatta. Nel 1647 si imbatté in una copia della Clavis Mathematicae di William Oughtred, un manuale che sostenne di aver letto in un paio di settimane. La Clavis era la più chiara e completa esposizione disponibile delle conoscenze dell’epoca riguardo alla matematica e all’algebra. Wallis l’apprese così approfonditamente da considerarsi discepolo di Oughtred.

Due anni dopo, il suo lavoro per le forze del Parlamento, oramai vittoriose, fu premiato con l’incarico di professore di geometria a Oxford, fatto straordinario se si considera che egli non aveva mai ricevuto un’educazione matematica formale né aveva mai pubblicato nulla. Fu senza dubbio una nomina “politica”, anche considerando che il suo predecessore era stato allontanato per il solo fatto di essere un realista. Wallis si dimostrò tuttavia degno dell’incarico ottenuto, che mantenne per i successivi quarant’anni in ogni contingenza politica. Non considerandosi “arrivato”, egli studiò tutto ciò che si conosceva in ogni branca della disciplina, e pubblicò negli anni alcune opere importanti sui più disparati argomenti matematici, come si vedrà in seguito. 

Il prestigio acquisito, e la sua presa di posizione contraria all’esecuzione di Carlo I all’inizio del 1649, fecero in modo che Wallis poté mantenere la cattedra anche dopo la Restaurazione della monarchia (1660-61), diventando persino cappellano di Carlo II. Continuò anche a decifrare messaggi criptati, questa volta per conto del re. 

Nel 1655 Wallis pubblicò un trattato sulla definizione analitica delle sezioni coniche, in cui per la prima volta esse venivano riconosciute come curve di secondo grado. In questo Treatise on the Conic Sections, Wallis popolarizzò il simbolo ∞ per indicare una quantità infinita. Così scriveva: 

“Considero che qualsiasi piano (seguendo la Geometria degli indivisibili del Cavalieri) sia costituito da un infinito numero di linee parallele, o, come preferirei, da un infinito numero di parallelogrammi della stessa altezza (sia l’altezza di ciascuno di essi una parte infinitamente piccola, 1/∞, dell’altezza complessiva, e il simbolo ∞ indichi l’infinito), e l’altezza di tutti assieme sia l’altezza della figura”. 

L’anno successivo (1656), diede alle stampe quello che viene considerato il suo capolavoro, l’Arithmetica Infinitorum, forse la più significativa opera sull’analisi prima che Leibniz e Newton ponessero le basi del calculus. Essa ebbe vasta risonanza, e diede un grande impulso alla matematica inglese. Il testo, che sistematizza ed estende i metodi di analisi di Cartesio e Cavalieri, contiene il risultato per il quale Wallis è soprattutto ricordato, cioè il prodotto infinito per π/2 (formula di Wallis):

Ma il suo valore consiste anche nei metodi e nelle notazioni innovativi per la soluzione degli antichi problemi di quadratura e cubatura. Fu in questa Aritmetica degli infiniti che egli introdusse la notazione standard per le potenze, estendendole dai naturali positivi ai numeri razionali:

Passarono quasi trent’anni prima dell’uscita di un’altra pubblicazione fondamentale del matematico inglese: il Treatise of Algebra (1685). L’opera, introdotta da un lungo preambolo storico sullo sviluppo della disciplina, contiene il primo uso sistematico delle formule fisiche. Una quantità data vi viene rappresentata dal rapporto numerico con l’unità di misura utilizzata per quel tipo di grandezza. La parte finale del trattato è dedicata ai contenuti e alle implicazioni dell’Arithmetica Infinitorum, con la descrizione dei contributi nel frattempo apportati al calcolo delle grandezze infinitamente piccole o grandi da Newton e da altri matematici.

Accanto al suo lavoro di matematico teorico, Wallis intraprese nel tempo anche l’opera di curatore delle edizioni postume di opere di altri matematici inglesi, come Oughtred (il suo maestro virtuale) e Thomas Harriot. Si dedicò inoltre alla traduzione di opere matematiche e scientifiche degli antichi greci, probabilmente intrapresa su manoscritti originali o su copie giunti a Oxford nel 1629, quando William Herbert, cancelliere dell'università, acquistò la collezione lasciata dal matematico veneziano Francesco Barozzi per 700 sterline e la donò alla Biblioteca Bodleiana, dove è tuttora conservata. Vero genio polivalente, Wallis redasse anche opere su soggetti quali la logica, la grammatica, la linguistica e la teologia. Come se non bastasse, fu tra i fondatori della Royal Society.

Un personaggio così straordinario non poteva sfuggire all’attenzione dei romanzieri. Iain Pears ne ha fatto uno dei quattro protagonisti del bellissimo thriller, colto e raffinato, La quarta verità (Longanesi, Milano, 1999, ora TEA, 2010), di cui mi sono occupato in un precedente articolo. Secondo uno dei testimoni di un misterioso omicidio di un docente del New College, compiuto a Oxford nel 1663, Wallis

“(…) non godeva di grandi simpatie, cosa ai miei occhi comprensibile dal momento che era stato Cromwell a imporlo a Oxford. Wallis era soprattutto impopolare perché, ai tempi della grande purga dei puritani seguita al ritorno del re, non soltanto aveva mantenuto la sua carica, ma aveva addirittura ricevuto segni di favore dalle alte sfere”. 

Nel corso della sua testimonianza epistolare, Wallis replica a queste critiche con la sua verità, che, nella finzione letteraria, gli rende forse un po’ di giustizia: 

“Sento di dovermi spiegare; non dico, badate, giustificarmi, dal momento che penso di essere stato coerente nel corso di tutta la mia carriera. So che i miei nemici non sono d'accordo, e suppongo che la ragionevolezza di quanto da me compiuto durante la mia attività pubblica - se tale si può definire - non sia chiara a menti poco informate. Com'è possibile, dicono, che un uomo sia anglicano, presbiteriano, leale al martire Carlo, e diventi poi il capo crittografo di Oliver Cromwell e decifri le lettere più segrete del re per aiutare la causa parlamentare, quindi torni alla Chiesa anglicana e, per finire, sfrutti le proprie capacità per difendere di nuovo la monarchia, una volta restaurata? Non è questa ipocrisia? Non è semplicemente un modo di mettersi al servizio unicamente dei propri interessi? Così dicono gli ignoranti. 

A tutto questo rispondo di no. Non lo è, e chiunque dileggi le mie azioni ignora quanto difficile sia riequilibrare gli umori di un sistema politico una volta che venga colpito da una malattia. C'è chi dice che ho cambiato bandiera da un giorno all'altro, e sempre per tornaconto personale. Ma davvero credete che in tal caso mi sarei accontentato della cattedra di geometria all'università di Oxford? Se fossi stato davvero ambizioso, avrei mirato quantomeno a una carica vescovile. Ho rinunciato a questa non perché, come potreste credere, mi sarebbe stato impossibile ottenerla: ma perché non era quello il mio obiettivo. A muovermi non era un'ambizione egoistica e mi sono adoperato al fine di essere utile piuttosto che grande. Ho fatto sempre di tutto per agire secondo principi di moderazione, in conformità con quella che al momento era l'autorità costituita. Sin da quando scoprii per la prima volta il disegno segreto della matematica e mi dedicai alla sua esplorazione, ho anelato all'ordine, perché è nell'ordine che si realizza il disegno divino. La gioia di un problema matematico risolto con eleganza e il dolore nel vedere l’armonia naturale dell'uomo infranta sono due facce della stessa medaglia; in entrambi i casi credo di essermi schierato a fianco della rettitudine. 

Né ho desiderato, quale ricompensa, fama o reputazione; anzi, le ho rifuggite in quanto vanità e ho accettato di buon grado che altri conquistassero cariche elevate nella Chiesa e nello Stato, sapendo che in realtà la mia influenza segreta aveva un peso di gran lunga maggiore della loro. Che gli altri parlino pure; il mio compito era agire e questo ho fatto al maglio delle mie capacità; ho servito Cromwell, perché solo lui, con il suo pugno di ferro, poteva riportare l'ordine nel Paese e porre fine alle dispute tra le fazioni, e ho servito il re quando, alla morte di Cromwell, quel ruolo sancito da Dio passò a lui. E sono stato un buon servitore per entrambi; non per loro in quanto tali, ovviamente, ma perché, così facendo, servivo il mio Dio, come ho cercato di fare in ogni cosa”.

Riconoscere nell’immenso il piccolo, quanta voluttà!

Otto anni dopo la morte di Jacob Bernoulli (1654-1705), nell’agosto 1713, fu pubblicato in latino a Basilea il testo, lasciato incompiuto, dell’Ars Conjectandi, l’opera che fondò il moderno calcolo delle probabilità, che conteneva una teoria delle permutazioni e delle combinazioni, i cosiddetti numeri di Bernoulli, dai quali egli ricavò le serie esponenziali, lo studio della prevedibilità matematica e morale, lo studio della probabilità con la cosiddetta legge dei grandi numeri. Assieme ai quattro libri sull’«arte di fare previsioni» basate sulla matematica nel campo dei giochi e della vita civile, sociale ed economica, il volume conteneva anche il Tractatus de seriebus infinitis, che costituiva una ristampa unitaria delle cinque “dissertazioni” sull’argomento pubblicate separatamente (ma concepite come un tutt’uno) dal matematico svizzero tra il 1686 e il 1704. Concludeva l’edizione una lettera in francese sul Jeu de Paume, un antenato del tennis. 

Una serie è la somma degli elementi di una successione (una lista ordinata di elementi, detti termini). Le successioni e le serie finite hanno il primo e l’ultimo termine definiti (ad esempio, i numeri naturali da 1 a 100), mentre le successioni e le serie infinite continuano indefinitamente (ad esempio i numeri pari). Nel secondo caso, data una successione infinita di numeri {a_n}, una serie è informalmente il risultato ottenuto sommando tutti i termini: a₁+ a₂+ a₃+ … L’operazione si può scrivere in modo più compatto utilizzando il simbolo Σ. Il risultato può essere un valore finito (allora la serie è detta convergente), può essere infinito (serie divergente), oppure, se il limite non esiste, la serie si dice indeterminata o oscillante.

Nel trattato sulle serie infinite, Bernoulli vuole dare una struttura euclidea alla teoria delle serie, cioè organizzarla come una successione di proposizioni derivate da certi assiomi. Sul modello degli Elementi di Euclide, egli basa il suo studio su diversi principi impliciti (ad esempio, la possibilità di estendere all’infinito regole valide per processi finiti) e su nozioni indefinite (così egli non fornisce una definizione di somma o di limite). Il testo inizia con tre assiomi: 

1. Ogni quantità può essere divisa in parti più piccole; 

2. Data una quantità finita, si può assumere una quantità che sia più grande di questa quantità; 

3. Data una quantità, se si toglie una sua parte e si sottrae da essa ciò che rimane, si ottiene quella parte (cioè: dato A, se A – B = C, allora A – C = B). 

Le prime due proposizioni sono: 

a) Una quantità più piccola di qualsiasi altra quantità è nulla; 

b) Una quantità più grande di qualsiasi altra quantità è infinita. 

Per dimostrare il primo teorema, Bernoulli sostiene che, se una quantità più piccola di qualsiasi altra quantità non fosse nulla, allora potrebbe essere divisa in parti più piccole e ciò è contrario all’ipotesi. Allo stesso modo, nel secondo teorema, se una quantità è più grande di qualsiasi altra quantità fosse finita, allora non potrebbe essere aumentata, il che è contrario all’assioma 2.

Dopo aver affermato che ogni progressione geometrica può essere continuata all’infinito, perché si possono aggiungere sempre nuovi termini (diversi da zero o da infinito), Bernoulli dimostra che: 

c) Date una progressione geometrica A, B, C, D, E e una progressione aritmetica A, B, F, G, H, se i primi due termini di entrambe le progressioni sono identici, allora i termini C, D, E di una progressione geometrica sono più grandi dei corrispondenti termini F, G, H della progressione aritmetica. 

Se poniamo A = 1 e B = 1 + a, questo teorema fornisce la disuguaglianza di Bernoulli: 

(1 + a)ⁿ > (1 + a) 

La dimostrazione di Bernoulli è la seguente. Dato che A : B = B = C, allora A + C > 2B = A + F e C > F. Inoltre:

A + D > B + C > B + F = A + G

Da cui D > G, e così via. 

Poi il matematico svizzero dimostra i due seguenti enunciati: 

d) Una progressione geometrica crescente a₁, a₂… può essere continuata fino a un termine a_n maggiore di ogni dato numero Z. 

e) Una progressione geometrica decrescente a₁, a₂… può essere continuata fino a un termine a_n minore di ogni dato numero Z.

Per dimostrare il teorema e), Bernoulli considera una progressione geometrica crescente b₁, b₂… tale che b₁ = Z e il rapporto b₁ : b₂ sia il reciproco del rapporto a₁ : a₂. Questa progressione può essere continuata fino a un termine b_n > a₁ (per l’enunciato d). Ora, continuando la progressione a₁, a₂… fino a a_n, dato che: 

e  a₁ <  b_n, si ottiene a_n < b₁ = Z 

Bernoulli fornisce anche due corollari ai due ultimi teoremi: 

f) L’ultimo termine di una progressione geometrica crescente è ∞. 

g) L’ultimo termine di una progressione geometrica decrescente è 0. 

Non si preoccupi il lettore: qui sopra ho riassunto solo le prime 3 delle 66 pagine del trattato! Nelle rimanenti, egli raggiunge altri importanti risultati, quali:

h) la somma della serie armonica è infinita, cioè:

è divergente (Bernoulli credeva che la dimostrazione fosse nuova, ma in realtà era già stata fornita dal bolognese Pietro Mengoli quarant’anni prima); 

i) la somma della serie dei reciproci dei numeri quadrati, vale a dire:

è convergente, ma Bernoulli non è in grado di trovare una forma chiusa (cioè una formula), perché è un problema “più difficile di quanto ci si aspettasse”, anche se riesce a dimostrare che essa converge a un limite finito più piccolo di 2. Egli afferma: “Se qualcuno la trova, ce la comunichi, perché il nostro sforzo è stato vano, e avrà tutta la nostra riconoscenza”. Fu in seguito Eulero, nel 1737, a ottenere la soluzione di questo che divenne noto come il problema di Basilea, calcolando che la somma converge a π² / 6. 

La seconda parte del trattato si intitola De usu serierum infinitarum in quadraturis spatiorum et rectificationibus curvarum, e riguarda le applicazioni dei suoi risultati sulle serie infinite, che egli utilizza per la rettificazione di alcune curve algebriche e il calcolo di alcune funzioni notevoli. Così, dopo aver introdotto il concetto di serie mista (in cui, date due serie, ciascun termine della prima è moltiplicato per il corrispondente termine della seconda), Bernoulli dimostra ad esempio come le serie infinite possano consentire di rettificare un arco di circonferenza o calcolare il logaritmo di un numero o, ancora, calcolare i punti su una curva catenaria o su una lossodromica. 

Naturalmente Jacob Bernoulli non era il solo a studiare le serie infinite, perché dell’argomento si erano già occupati, tra gli ultimi, Pietro Mengoli e l’olandese Christiaan Huygens. Nello stesso periodo Gottfried Wilhelm von Leibniz, il suo maestro, gli inglesi John Wallis e, naturalmente, Isaac Newton stavano ponendo le basi del calcolo infinitesimale, il Calculus per eccellenza. Eppure, in tutti questi uomini, man mano che procedevano le scoperte, rimaneva un senso di meraviglia per il fatto che una somma infinita potesse dare un risultato finito o che proprio il calcolo di grandezze estremamente piccole potesse rivelare connessioni inaspettate tra campi diversi come l’algebra, la geometria o la teoria dei numeri. 

Questo sentimento è bene espresso dalla poesia in latino che Bernoulli volle porre a conclusione e commento del suo trattato: 

Come una serie infinita cinge una finita 

sommetta, e nell'illimitato un limite esiste: 

così persistono le vestigia dell’immensa divinità

in un piccolo corpo e nell'angusto limite il limite scompare. 

Riconoscere nell'immenso il piccolo, quanta voluttà! 

Nel piccolo l’immenso Dio discernere, quanta! 

Nota: La traduzione è mia, mi perdonino i latinisti, perché quella fornita da Piergiorgio Odifreddi non mi è sembrata abbastanza fedele; inoltre, “numinoso”, termine inventato dallo storico delle religioni e teologo Rudolf Otto nel 1917, poco ci coglie in un’opera della fine del Seicento.