La guerra italiana contro la malaria

 

Il grande storico francese Fernand Braudel scrisse poco prima di morire che «Sebbene pericolosa, la peste, importata dall'India e dalla Cina attraverso relazioni a distanza, è una straniera temporanea nel Mediterraneo. La malaria ha lì una sede permanente. Fa da sfondo al quadro della patologia mediterranea». In effetti, la presenza della malaria in ampie porzioni del territorio italiano è ampiamente documentata fin da tempi molto antichi e il flagello era endemico già ai tempi dell'antica Roma.

La malaria, che ogni anno mieteva migliaia di vittime, era tra i problemi sanitari più urgenti e gravi che il governo dell’Italia unita si trovò ad affrontare, perché riguardava ampie zone del territorio, desolate, inabitabili e improduttive proprio a causa della malattia. Particolarmente colpite erano le campagne intorno a Roma, l’agro pontino, la Maremma toscana, la Sardegna, il Veneto, la Romagna, la Puglia, la Calabria, la Basilicata, anche se nel passato più remoto ci sono stati sicuramente periodi in cui l'influenza della malaria aveva coperto estensioni territoriali molto più ampie, sia per il cambiamento delle condizioni climatiche, sia per le variazioni della dinamica delle popolazioni, sia per eventi storici che avevano causato l'abbandono dei lavori di regolazione idraulica nelle zone soggette a impaludamento.

Del problema non si ebbe un quadro preciso fino all’inchiesta agraria promossa dalla Camera dei deputati negli anni 1877-1886, che mise in luce le miserevoli condizioni delle popolazioni nelle campagne. La stima del numero dei colpiti dalla malaria era impresa non facile, perché le distanze, la distribuzione frammentata della popolazione, la mancanza di presidi medici, rendevano complicato un conteggio preciso.

Nel 1882 il senatore valtellinese Luigi Torelli, più volte ministro, si occupò del problema: stilò la prima bozza di una carta geografica in cui erano segnalate le aree italiane colpite da malaria; delle 69 province, solo 6 erano completamente esenti dal morbo, mentre 21 presentavano territori con malaria gravissima, 29 con malaria grave, 13 con malaria leggera; risultava inoltre che le zone colpite erano anche quelle più fertili, tanto che Torelli stimò che circa due milioni di ettari di terreno coltivabile erano lasciati incolti e altrettanti venivano sfruttati in modo insufficiente; negli stessi anni fu valutato che il numero di morti annuali dovuto direttamente alla malattia si aggirava intorno ai ventimila, a cui si dovevano aggiungere i morti causati da complicazioni dovute al morbo.

Un aspetto importante riguarda infatti la struttura della mortalità registrata nelle aree malariche, che è solo in parte attribuibile ai decessi direttamente causati da questa malattia. Infatti, lo stato di debilitazione causato dalla malaria, anche quando questa infezione non è direttamente mortale, rende i soggetti malarici più facilmente preda di altre forme morbose (legate principalmente all'apparato respiratorio e gastrointestinale). D’altra parte, un attacco di malaria (soprattutto in caso di recidive) può aggravare altri tipi di infezioni già in corso. Inoltre, i figli di madri malariche nascevano spesso sottopeso e, anche se non contraevano la malaria, erano soggetti a rischi eccezionalmente elevati di morte, anche dopo il primo anno di vita, soprattutto per infezioni gastrointestinali e polmonari, come la tubercolosi.

Inizialmente, per spiegare le ragioni dell’infezione, si pensò che fossero i terreni paludosi a produrre la malattia, ma se questo poteva essere plausibile per il Nord, dove gli acquitrini abbondavano, non poteva valere per il Sud: in molte zone non paludose, era sufficiente il calore e un piccolo grado di umidità per favorire la “fermentazione” del terreno (la “mal aria”) e dar luogo alla malattia. Nel tentativo di arginare il problema, furono progettati interventi di bonifica a partire dall’Agro romano, che lambiva la capitale. La prima legge in materia fu promossa dall'ingegnere e deputato Alfredo Baccarini (1826-1890, Legge 25 giugno 1882, n. 269) con la quale lo stato, consapevole dei limiti dell'azione dei privati, perseguì un intervento organico di impegno sociale e sanitario contro la malaria. La bonifica avrebbe dovuto provvedere al prosciugamento e al risanamento dei laghi, degli stagni, delle paludi e delle terre paludose.

Negli ultimi trent'anni dell’Ottocento, un folto gruppo di scienziati italiani, come Giovanni Battista Grassi, Angelo Celli, Camillo Golgi, Ettore Marchiafava, Amico Bignami, Giuseppe Bastianelli, si impegnò per risolvere l’enigma della malaria e divenne noto come gruppo romano di malariologia, perché la maggior parte delle persone coinvolte lavorava a Roma e molte delle ricerche cliniche sull’argomento furono realizzate presso l’ospedale Santo Spirito della capitale, che ospitava degenti maschi provenienti dalle zone malariche vicine e nei momenti critici giungeva a curare fino a mille degenti.

Negli anni 1878 e 1879, due eminenti patologi, Corrado Tommasi-Crudeli (1834-1900) e il tedesco Edwin Klebs (1834-1913), decisero di unire le loro forze per studiare insieme la causa della malaria nell’agro romano e per questo furono ospitati da Stanislao Cannizzaro nel laboratorio di chimica di Roma. I due isolarono dal suolo delle zone paludose un microbo, da loro chiamato Bacillus malariae, e pubblicarono due memorie negli atti della Regia accademia dei Lincei, sostenendo che il germe si rinveniva nelle zone malariche e poteva essere coltivato in laboratorio; asserirono inoltre che, inoculato nei conigli, procurava febbre e ingrossamento splenico.

Ettore Marchiafava (1847-1935), allievo di Tommasi-Crudeli, rinvenne organismi simili a quelli descritti da Tommasi Crudeli e Klebs nel sangue di tre individui morti per malaria perniciosa; nella loro milza e nel midollo osseo era inoltre presente un pigmento nerastro simile a quello riscontrato dai colleghi nei conigli, lo stesso pigmento presente negli organi di individui deceduti per malaria e che già altri avevano descritto, attribuendolo ad accumuli di melanina. Sembrava che la malaria avesse finalmente trovato la sua causa (un batterio).

Nel 1880, il maggiore medico francese Charles Louis Alphonse Laveran (1845 – 1922), ex studente di Pasteur, che dal 1878 lavorava presso l’ospedale militare di Costantina, in Algeria, rese noto di aver analizzato il sangue prelevato da numerosi ricoverati malarici. Mentre le autopsie mettevano tutte in evidenza la tipica pigmentazione bruna, nel sangue prelevato da individui vivi poté osservare che i leucociti erano colmi di melanina e erano presenti cellule di dimensioni variabili e dotate di movimento ameboide, libere o aderenti ai globuli rossi; osservò inoltre cellule flagellate, dotate di movimenti rapidi. Le sue comunicazioni, però, destarono inizialmente scarsa eco, in quanto, sull’onda delle scoperte batteriologiche, non si poteva pensare che una malattia fosse provocata da protozoi; tuttavia, un altro medico, Eugène Richard, che lavorava in un ospedale vicino a quello di Laveran, confermò le sue osservazioni. Il lavoro di Laveran, Traité des fièvres palustres, fu pubblicato nel 1884.

Nel frattempo, in Italia non tutti erano d’accordo con le conclusioni di Tommasi-Crudeli e Klebs. Uno dei più convinti oppositori della teoria batterica era da tempo Guido Baccelli (1830-1916), professore di clinica medica presso l’Università di Roma e in seguito anche senatore e ministro, che da anni sosteneva che la malattia era dovuta a un’infezione dei globuli rossi e nel 1878 aveva pubblicato su incarico del Governo l’ampio trattato La malaria di Roma, presentato all’Esposizione universale di Parigi.

Si decise allora di ricorrere al giudizio di Camillo Golgi (1843-1926), che in seguito (1898) avrebbe scoperto l’organulo cellulare che da lui prende il nome, premio Nobel per la Medicina (1906), la cui fama di istologo era ormai da tempo consolidata, e al parassitologo Edoardo Perroncito (1847-1936). Un gruppo di scienziati, coordinati da Perroncito e Golgi, ripeterono a Pavia gli esperimenti, utilizzando il protocollo di Tommasi-Crudeli e Klebs, che prevedeva un esame istologico condotto qualche ora dopo il prelievo, ma ottennero risultati ambigui; si poteva pensare che il ritardo nell’osservazione avesse contaminato il prelievo. Batteri simili a quelli rinvenuti da Tommasi-Crudeli e Klebs, vennero infatti rinvenuti anche in sangue prelevato da soggetti sani. Nel frattempo, Marchiafava, nel 1882, aveva conosciuto Laveran, che si era recato a Roma per verificare presso l’ospedale Santo Spirito se anche i malarici dell’agro pontino presentavano nel sangue gli organismi da lui osservati in Algeria; il medico francese aveva mostrato i preparati al collega, che da quel momento aveva cominciato a nutrire seri dubbi sulle conclusioni di Tommasi - Crudeli. Marchiafava e l’igienista Angelo Celli (1857–1914) ripresero ad analizzare numerosi campioni di sangue di persone con la malaria e infine i due, che disponevano di mezzi tecnici migliori, poterono confermare che il responsabile della malattia era un protozoo, da loro denominato Plasmodium e non un batterio; i loro risultati vennero suffragati dalle osservazioni degli assistenti di Marchiafava, Bignami e Bastianelli. La causa della terzana maligna, il Plasmodium falciparum, fu infine individuato nel 1889 da Marchiafava e Celli, in seguito all’ideazione di un metodo di colorazione ottimale per identificare i parassiti negli strisci di sangue; si chiarì, in questo modo, che quasi esclusivamente al P. falciparum erano attribuibili le forme cliniche delle febbri e gli episodi mortali di malaria. La comunità scientifica, così, si convinse che Laveran, Marchiafava, Bignami e Bastianelli avevano ragione; i riscontri clinici ottenuti da Tommasi-Crudeli e Klebs potevano essere attribuiti a infezioni non riconducibili alla malaria.

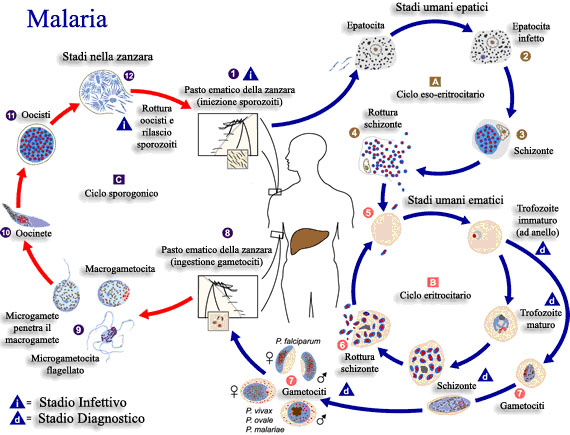
C’era ora da capire se la periodicità con cui si manifesta l’attacco febbrile (le febbri malariche hanno accessi periodici per cui si distinguono la terzana, la quartana e altre forme periodiche meno diffuse) fosse provocata da due o più distinte specie di plasmodio, oppure se lo stesso parassita provocasse sintomatologie diverse in base a non meglio specificati fattori ambientali.

Camillo Golgi, che continuava ad interessarsi al problema, studiò numerosi pazienti, ponendo particolare attenzione alle variazioni della loro temperatura e prelevò loro il sangue a intervalli regolari sia durante gli accessi febbrili che nei periodi di remissione. L’osservazione al microscopio gli permise di notare che nel caso di malati affetti da quartana, i corpi pigmentati raggiungono il loro pieno sviluppo nell’intervallo fra i due accessi febbrili; inizia allora la divisione cellulare del parassita e subito dopo la temperatura del paziente si innalza. Nel 1885 dimostrò che i due diversi tipi di febbre malarica, la terzana e la quartana, sono provocati da due specie di plasmodio diverse: Plasmodium vivax, responsabile della terzana benigna, e Plasmodium malariae, responsabile della quartana. Nel 1889 dimostrò che gli attacchi febbrili si verificano nel momento in cui i merozoiti (stadio del ciclo del plasmodio) rompono i globuli rossi e si liberano nel circolo sanguigno. Gli accessi febbrili si manifestano nel momento in cui le cellule del parassita, riprodottesi all’interno del globulo rosso umano (fase di sporulazione), distruggono l’emazia, fenomeno che nella terzana avviene ogni 48 ore, nella quartana ogni 72; fuoriuscite nel plasma, si immettono in nuovi globuli rossi, aumentando il livello di infestazione. La precisa classificazione delle due specie, P. malariae e P. vivax si deve a Giovanni Battista Grassi (1854-1925) e al suo assistente Raimondo Feletti, mentre nel 1897, l’americano William H. Welch (1850 – 1934) descriverà il P. falciparum e infine nel 1922, John W. W. Stephens il P. ovale.

Dal punto di vista clinico, gli studi di Golgi permisero di formulare una diagnosi rapida e precisa della presenza della patologia e la somministrazione del chinino qualche ora prima dell'accesso febbrile permise di evitare la riproduzione del plasmodio, liberando il paziente dall’infezione. Nel 1894 Bignami e Bastianelli riprodussero i sintomi della malaria in un volontario sano, iniettandogli per via intradermica una goccia di sangue prelevato da un paziente malarico.

Bisognava comprendere come la malattia venisse trasmessa all’uomo; era questa la chiave per poter attuare un intervento preventivo efficace. Da tempo, in molti pensavano che le zanzare fossero in qualche modo coinvolte nella trasmissione della malattia; agli inizi del Settecento Giovanni Maria Lancisi aveva suggerito che fosse un liquido velenoso inoculato dalla zanzare a produrre le febbri e aveva consigliato di prosciugare le zone in cui vi era ristagno di acqua, luoghi ideali per lo sviluppo delle larve. Nel frattempo, si cominciavano a scoprire molte malattie trasmesse da invertebrati e in molti casi era stato individuato il ciclo completo di molti parassiti.

La scoperta più interessante per l’avanzamento delle indagini sulla malaria era stata fatta a Taiwan dal medico scozzese Patrick Manson (1844-1922), fondatore della medicina tropicale, che per la prima volta aveva verificato che una parassita, la filaria, poteva essere ospitato da un insetto, la zanzara Culex fatigans. Forte di questa scoperta, avanzò l’idea che qualcosa di simile avvenisse anche per il plasmodio: il globulo rosso protegge i parassiti dall’attacco dei globuli bianchi e può penetrare, quando questa punge l’uomo, nella zanzara, dove il parassita potrebbe completare il suo ciclo. Tornato nel Regno Unito, Manson divenne insegnante medico e consigliere del British Colonial Office; in questa veste, conobbe nel 1894 Ronald Ross (1857 – 1932), ufficiale medico dell’Indian Medical Service e pensò che questi, a contatto con zone dove la malaria era molto diffusa, avrebbe potuto trovare riscontri alla sua teoria. Fra Manson e Ross si stabilì una fitta corrispondenza: Manson insisteva perché l’amico “seguisse i flagelli” che si trovavano negli ammalati, nei tessuti delle zanzare, mentre Ross lo teneva informato dei suoi progressi.

Ma quali zanzare? Ross non era uno zoologo e le sue conoscenze sui vari generi di zanzara erano piuttosto approssimate: inizialmente ebbe anche difficoltà a fare le prime dissezioni sugli insetti e comunque non annotò con precisione su quali specie conducesse i suoi esperimenti. Andando alla cieca, rivolse le sue iniziali attenzioni su generi non coinvolti nell’infestazione (Aedes e Culex), come del resto stavano facendo negli stessi anni nei laboratori romani, non ottenendo risultati.

Nel frattempo, anche Grassi, Bignami e Celli stavano cercando di risolvere l’enigma; puntando sull’ipotesi dell’inoculazione, che stava acquistando sempre maggior credito rispetto a quella secondo cui stadi immaturi del parassita potevano essere presenti nel terreno, cercavano di trasmettere la malaria, facendo pungere da zanzare allevate in laboratorio individui malarici e poi liberando le stesse zanzare in stanze con volontari sani per verificare se in essi si sviluppasse la malattia; lavorando con le Culex, però, i risultati ottenuti erano sempre negativi. Nella primavera del 1898 Grassi intuì quale era stato l’errore in cui erano incorsi fino ad allora: non diverse specie di zanzare potevano disseminare la malattia, ma una sola.

L’idea di Grassi era semplice: dal momento che gli uomini si muovono nelle varie regioni italiane, mentre i luoghi malarici hanno una localizzazione costante, la causa della malattia deve essere legata soprattutto alla distribuzione di una determinata specie di zanzara nelle zone malariche, dato che zone con condizioni ambientali simili possono non presentare la malattia. Del resto, in Italia erano da tempo note zone infestate da zanzare, ma in cui la malaria non era presente. Nell’agosto del ‘98, Grassi aveva risolto il problema e identificato negli “zanzaroni” (Anopheles claviger) i vettori della malaria.

Naturalmente, completate le indagini biogeografiche, restava da verificare che effettivamente negli zanzaroni avviene una parte del ciclo del plasmodio. Grassi, allora, chiese aiuto a Bignami e Bastianelli, che accettarono di seguire il suo protocollo sperimentale; Grassi si sarebbe occupato di procurare gli zanzaroni, con cui sarebbero stati punti individui sani, mai vissuti in zone malariche. In novembre si fece l’esperimento fondamentale: un soggetto sano fu punto dalle zanzare sospette, sviluppò la malattia e guarì una volta che gli fu somministrato il chinino.

Del chinino, estratto dalla corteccia dell'albero della china di origine andina, erano note le proprietà antifebbrili sin dal Seicento. Antonio de la Calancha, un gesuita vissuto nel XVII secolo in Sud America, scrisse nel 1633 di un "albero che chiamano "l'albero della febbre" la cui corteccia trasformata in una polvere (...) e data come bevanda, guarisce le febbri e le terzane”. Il nome Inca di questo albero era quina, ma non ci sono prove che essi riconoscessero il suo valore per il trattamento della malaria, ma semplicemente la sua capacità di prevenire i brividi indotti dal freddo. Furono i missionari gesuiti i primi a usare la corteccia d'albero polverizzata per curare la malaria e così divenne nota come “polvere dei gesuiti”. Il cardinale Juan de Lugo ne aprì la strada all'uso a metà del XVII secolo a Roma. Nel 1742, Linneo gli diede il nome “chinchona”, probabilmente perché aveva sentito la leggenda della contessa di Chinchon, moglie del viceré spagnolo di Lima, che sarebbe stata guarita dalla malaria grazie all'uso della corteccia in polvere.

Nel corso dei decenni successivi furono fatti diversi tentativi per isolare un principio attivo puro dalla corteccia di china, ma tutti fallirono. Nel 1819 Friedrich Ferdinand Runge isolò quella che chiamò "base cinese", e un anno dopo Pierre-Joseph Pelletier e Joseph-Bienaimé Caventou estrassero una sostanza dalla corteccia della Cinchona cordifolia con acido seguito da neutralizzazione con alcali e ottennero una sostanza identica alla “base cinese”, che chiamarono chinino. Campioni di questo alcaloide della china furono messi a disposizione dei medici negli ospedali di Parigi e presto molti di loro riferirono dell'efficacia del chinino come trattamento per la malaria.

Il problema fondamentale per i chimici che tentarono di isolare il principio attivo del chinino fu che esso fa parte di un gruppo di isomeri difficilmente distinguibili. Intorno al 1853, Louis Pasteur, trattò la polvere di Chinchona con acido solforico diluito, che diede un nuovo prodotto di degradazione che in seguito fu chiamato chinotossina. Il passo fondamentale per svelare la chimica alla base di questa degradazione fu infine compiuto nel 1908 dal chimico tedesco Paul Rabe, che ne dedusse correttamente la struttura. Il chinino è stato da tempo sostituito da farmaci sintetici meno tossici come la mepacrina (1932), la clorochina (1939), la primachina (1946), la meflochina (1979) e i derivati dell'artemisinina dalla pianta cinese Artemisia annua, ma è tuttora utilizzato come aroma alimentare nelle acque toniche e nella preparazione di vari aperitivi e digestivi.

Al chiudersi del 1898, però, molti erano ancora i problemi da risolvere: le diverse febbri malariche si sviluppano avendo come vettore la stessa specie di zanzara? Come e dove gli insetti si infettano? Solo nell’uomo o anche in altri animali si completa il ciclo di sviluppo del plasmodio? Tra il 1899 e il 1902 il gruppo romano dimostrò che il ciclo vitale del plasmodio si completa all’interno del corpo dell’insetto - in cui avviene la riproduzione sessuale -, mentre nell’uomo avviene la riproduzione asessuata. I ricercatori dimostrarono inoltre che le larve sono sempre immuni, e quindi la malattia non può essere ereditaria; solo le femmine di alcune specie di anofeli veicolano la malattia e se non esistono uomini affetti da malaria, la regione ne è esente.

Il governo italiano si mosse tempestivamente per promuovere interventi antimalarici, anche grazie all’elevato livello scientifico della compagine parlamentare, in cui erano presenti, sia fra i deputati che fra i senatori, medici, igienisti, esperti in malattie del lavoro; dalla fine degli anni Novanta a tutta l’età giolittiana, inoltre, anche il livello scientifico della burocrazia italiana era altissimo e collaborò all’impresa di risanamento in piena sintonia con i medici, che segnalavano una situazione drammatica. Angelo Celli, che era stato eletto alla Camera dei Deputati nel 1892, presentò agli inizi del Novecento una proposta di legge molto articolata e moderna. Per parte sua, il medico e istologo Giulio Bizzozero (1846-1901), mentore e maestro di Golgi, nominato in Senato nel 1890, nel suo intervento sulla proposta sottolineò come il chinino non fosse soltanto un mezzo di cura, ma dovesse anche essere utilizzato per prevenire la malattia: dato che la malaria viene trasmessa da una persona all’altra per mezzo delle zanzare, che ricevono il parassita da un malato e lo immettono in un altro, il soggetto malarico è pericoloso come qualunque persona affetta da malattia infettiva, per cui spetta allo Stato predisporre i mezzi per impedire il contagio. Lo stesso Grassi intervenne in molti suoi scritti, definendo il chinino indispensabile alle popolazioni delle zone malariche come l’acqua e l’aria; la sua somministrazione, dunque, doveva essere fornita gratuitamente.

Si rendeva necessario che lo Stato assumesse il monopolio di produzione del farmaco in modo da evitare abusi da parte di eventuali speculatori; per rendere facile l'acquisto del prezioso medicinale anche nei territori più isolati e arretrati, doveva essere venduto non soltanto nelle farmacie, ma anche presso gli spacci di sali e tabacchi; la cosa sollevò le proteste della potente categoria dei farmacisti, ma le insistenze dei medici ricercatori fecero sì che ottenesse l’approvazione del parlamento. Il chinino, inoltre, sarebbe stato distribuito a prezzo di favore alle pubbliche amministrazioni e alle imprese a rischio, purché venisse somministrato gratuitamente ai dipendenti; il suo prezzo sarebbe stato contenuto e i proventi per la sua vendita sarebbero stati reinvestiti per la battaglia antimalarica.

Nel disegno di legge passò l’idea che la cura con il chinino era un vero e proprio rimedio sociale e pertanto doveva essere distribuito gratuitamente per mezzo del medico comunale o uno specifico ufficiale sanitario e a tale proposito in seguito si decise che i comuni potessero consorziarsi per il mantenimento degli ufficiali sanitari. La malaria contratta nei luoghi di lavoro, nel caso che procurasse morte o inabilità, doveva essere considerata alla stessa stregua di un infortunio sul lavoro; i proprietari terrieri erano invitati a utilizzare le reticelle metalliche, per impedire alle Anopheles di penetrare nelle abitazioni e si stanziavano sussidi per coloro che avrebbero provveduto in tal senso; le reticelle, comunque dovevano essere presenti, nelle zone malariche, nelle stanze occupate dalle guardie di finanza, del personale addetto alle strade, nei locali per il servizio ferroviario e in quelli dei consorzi di bonifica. In realtà, in un territorio dove molte famiglie vivevano ancora in capanne di frasche e fango, sprovviste di finestre, le zanzariere erano improponibili (quando non venivano usate impropriamente per passare il pomodoro per la salsa o per rudimentali grill). Il trattamento con il chinino sembrava la via più facile e diretta per eradicare il morbo.

Al chiudersi del secolo, il governo operò in due direzioni: mise a punto leggi che proseguivano quanto già iniziato a partire dagli anni Ottanta per favorire il risanamento del territorio nazionale attraverso mezzi tecnico-idraulici e agronomici, e promosse l’uso del chinino, non solo come cura, ma anche per la prevenzione dell’infestazione.

La legge sul chinino di Stato fu approvata il 4 luglio 1895 grazie all'iniziativa parlamentare del deputato ed editore Federico Garlanda. Al deputato padovano Leone Wollemborg, fondatore della prima cassa rurale italiana, si deve la legge "Provvedimenti per agevolare lo smercio del chinino" del 23 dicembre 1900.

Su espressa richiesta parlamentare di Celli, la produzione di chinino venne affidata alla Farmacia centrale militare di Torino, che si approvvigionava annualmente di solfato di chinina per produrre tavolette compresse, poi distribuite nelle farmacie e negli spacci. La vendita al pubblico su tutto il territorio nazionale iniziò a partire dal 1903 e, dal momento che la malaria era stata definita malattia professionale, fu fatto obbligo ai datori di lavoro (proprietari terrieri, aziende ferroviarie, appaltatori di opere pubbliche che si svolgevano in territori malsani) di pagare una tassa proporzionale al numero di dipendenti; in questo modo fu sancito il principio del diritto dei poveri e degli operai ad avere gratuitamente il chinino profilattico e curativo. Spettava ai comuni promuovere nei loro territori la campagna antimalarica e far sì che fossero presenti strutture sanitarie idonee per la somministrazione del farmaco. Molti, fra cui lo stesso Grassi, avrebbero preferito che le spese per il consumo e la somministrazione del chinino fossero sostenute dallo Stato, mentre Celli, conscio delle resistenze che questa decisione avrebbe provocato, mediò fra le diverse esigenze. Lo Stato emanò anche precise disposizioni - del resto già presenti a partire dal 1865 - che imponevano ai proprietari terrieri di intervenire con lavori di scolo, di bonifica e miglioria dei terreni, assicurando ai proprietari dei terreni bonificati l’esenzione dall’imposta fondiaria per vent’anni.

La campagna, partita con tanto entusiasmo, si trovò di fronte a difficoltà insormontabili, legate soprattutto al fatto che moltissimi comuni, soprattutto nel Sud, non potevano fornire un servizio adeguato perché non erano finanziariamente in grado di assumere personale specializzato, o retribuivano con salari talmente bassi i medici condotti, che essi erano costretti a esercitare anche la libera professione, dedicando ben poco tempo alla campagna antimalarica. La popolazione, inoltre, era dispersa su ampi territori, per cui raggiungere i pazienti malati era estremamente difficile e i contagiati, per parte loro, difficilmente si recavano dal medico, sia perché il tragitto era troppo lungo, sia perché non avevano fiducia nella terapia.

Si decise allora di ricorrere all’istituzione di una “stazione sanitaria rurale” (dispensario) che aveva il compito di raccogliere dati statistici sull’entità del problema: doveva verificare quanti erano nella zona le persone infette e quante quelle sane, attraverso il prelievo e l’esame di campioni di sangue, per stabilire quale tipo di infestazione fosse stata contratta e poi decidere come e quando somministrare l’adeguata terapia preventiva o curativa. La stazione sanitaria era spesso affiancata da distaccamenti mobili che battevano la zona alla ricerca della popolazione da esaminare. Nei dispensari lavoravano spesso giovani medici, convinti sostenitori delle teorie di Celli e Grassi che ben presto si resero conto che perché la campagna antimalarica giungesse a buon fine era necessario convincere i contadini e gli operai, e per far questo era fondamentale rendersi utili in modo più diretto, curando altre malattie e consigliando semplici norme igieniche.

Grazie a questi provvedimenti, la mortalità a causa della malaria calò drasticamente, passando da circa 16.000 vittime nel 1895 a 7.838 decessi nel 1905.

Nel primo decennio del ventesimo secolo furono promulgati ben ventidue provvedimenti legislativi che affrontarono il modo per attuare efficacemente le opere di bonifica; dalla lettura dei provvedimenti, emerge come i legislatori fossero sensibili alle conseguenze igienico sanitarie di tali interventi.

Prima dello scoppio della guerra, in molte province italiane la malaria sembrava finalmente controllabile: a fronte di una mortalità di 490 individui ogni milione di abitanti nel 1900, si giunse nel 1914 a 57 morti, anche se i dati erano approssimati per difetto, in quanto spesso, per esempio, la mortalità infantile non veniva registrata e inoltre non si teneva conto delle persone che la malaria rendeva inabili al lavoro, numero non diminuito nel tempo. Lo scoppio della prima guerra mondiale, con i soldati al fronte in zone paludose e malariche, favorì un riacutizzarsi del morbo. Dopo la disfatta di Caporetto, gli austriaci che dal 1917 erano nelle aree del Piave, con la volontà di ostacolare il passaggio all'esercito italiano nel 1918 al loro ritiro lasciarono dietro di sé ingenti danni: nel basso Piave, dove era stata debellata la malaria, per 1/3 si ebbe una recrudescenza.

Con l'avvento al governo del Partito Nazionale Fascista la lotta per la bonifica divenne nella propaganda la bellicosa "guerra alle acque”, ma, pur favorendo i grandi investimenti, la bonifica agraria entrò in contrasto con il sistema feudale del latifondo. Le proteste dei latifondisti meridionali, che furono anche ricevuti da Mussolini, ottennero le provvisorie dimissioni del sottosegretario all'agricoltura Serpieri e la limitazione delle sanzioni sugli espropri. Continuava anche il contrasto alla malaria: per intervento diretto di Mussolini veniva autorizzata la sperimentazione sulle persone di nuove terapie. Giacomo Peroni e Onofrio Cirillo operarono su duemila operai dell'Opera Nazionale Combattenti in Toscana e Puglia, separati in due gruppi di studio. Nel primo fu sospesa ogni cura con il chinino per osservarne il decorso, mentre il secondo era trattato con iniezioni intramuscolari di "smalarina" (farmaco antimalarico a base di sali di mercurio e antimonio messo a punto dal medico sardo Guido Cremonese, docente di igiene alla regia università di Roma). L'esperimento, che si basava sulla constatazione che le persone curate per la sifilide non si ammalano di malaria (e soprattutto sul fatto che il commercio mondiale del chinino era controllato dagli olandesi) fu concluso nel 1929 dichiarando risultati positivi, ma un nuovo esame del Consiglio superiore di sanità su 395 persone in Sardegna ne sancì la tossicità.

Zone di endemismo malarico sono rimaste in Italia sino agli anni Sessanta dello scorso secolo, lungo delta del Po, in Sardegna e nell’Agro Pontino. Solo l’introduzione del controverso DDT dopo la Seconda guerra mondiale ha portato al totale sradicamento di questa malattia in Italia, nel resto d’Europa, negli Stati Uniti e negli altri paesi industrializzati. Nei paesi più poveri è tuttora responsabile di centinaia di migliaia di morti.

Beppo Levi, tra Torino, gli Appennini e le Ande

 

Beppo Levi (1875-1961) è stato un matematico autore di articoli su logica, equazioni differenziali, variabili complesse, sul confine tra analisi e fisica.

La famiglia di Beppo Levi era ebrea, e Beppo era il quarto di dieci figli. Il padre, Giulio Giacomo Levi, esercitava la professione di avvocato, ma fu anche autore di diversi libri su questioni politiche e sociali in cui manifestava le sue idee liberali messe in discussione dal nascente socialismo.

Studiò matematica all'Università di Torino, iniziando gli studi nel 1892. Frequentò i corsi tenuti da Corrado Segre, Enrico D'Ovidio e Giuseppe Peano, e questi matematici ebbero una grande influenza su di lui. Per tutti conservò un profondo affetto per il resto della sua vita.

Ebbe come maestri anche Vito Volterra e Mario Pieri. Corrado Segre, che aveva studiato a Torino con D'Ovidio, era stato nominato nel capoluogo piemontese alla cattedra di Geometria Superiore nel 1888. Divenne relatore della tesi di Levi,. Studió “...la varietà delle secanti delle curve algebriche, in vista dello studio delle singolarità delle curve spaziali”. Sono del 1897 e del 1898 una sua ampia memoria pubblicata dall'Accademia delle Scienze di Torino «Sulla varietà delle corde di una curva algebrica» e alcune note dei Rendiconti dei Lincei, in cui fra l'altro viene dimostrata la possibilità di mutare una data curva algebrica sghemba in un'altra priva di singolarità puntuali per mezzo di trasformazioni birazionali dello spazio e viene studiata la riduzione delle singolarità di una superficie algebrica mediante successive trasformazioni quadratiche. Ancora giovanissimo, Beppo Levi conquistò così un posto d'onore nel campo della geometria algebrica.

Negli ultimi tre anni di studio all'Università di Torino, Levi era sostenuto da una borsa di studio. Laureatosi nel luglio 1896, Levi fu nominato assistente di Luigi Berzolari a Torino e mantenne questo incarico fino al 1899. Suo padre era morto nel 1898 e questo diede a Levi la responsabilità di capofamiglia (era il figlio maggiore superstite). Per mantenere se stesso e gli altri membri della famiglia, assunse diversi incarichi di insegnante nelle scuole superiori. Insegnò prima a Sassari, poi a Bari, passando poi a Vercelli prima di insegnare in Emilia-Romagna, prima a Bobbio poi a Piacenza. Alcuni di questi incarichi lo portavano lontano dalla sua famiglia, cosa che lo angosciava e cercava di trovare lavoro più vicino alla sua città natale. Ritornò a Torino, dove insegnò all'Istituto Tecnico fino al 1906 quando il suo incarico venne reso permanente.

Durante questi sette anni come insegnante, Levi aveva tentato di ottenere diversi incarichi universitari ma senza riuscirci. Nel 1901, ad esempio, partecipò al concorso per la cattedra dell'Università di Torino indetto da Luigi Berzolari. In questa competizione arrivò terzo: il posto andò a Gino Fano.

Nel 1906 vinse il concorso per la nomina a professore di Geometria descrittiva e proiettiva all'Università di Cagliari. Mentre era sull’isola, Levi realizzò un lavoro eccezionale sull'aritmetica delle curve ellittiche che pubblicò in quattro articoli intitolati “Saggio per una teoria aritmetica delle forme cubiche ternarie” (un articolo nel 1906 e tre nel 1908). Riferì di questo lavoro nella conferenza “Sull'equazione indeterminata del terzo ordine” al Congresso Internazionale dei Matematici di Roma nel 1908. Rimase a Cagliari, insegnando geometria analitica, per quattro anni finché fu chiamato alla cattedra di analisi algebrica presso l'Università di Parma nel 1910. Mentre era a Cagliari, Levi aveva sposato Albina Bachi di Torre Pellice in Piemonte. Albina, come Levi, era ebrea; ebbero tre figli, Giulio, Laura ed Emilia. Anche se per Albina “...Cagliari era una località esotica; per lui era troppo lontano dalla sua famiglia”.

L'anno in cui Levi lasciò Cagliari era stato promosso a professore ordinario, ma era così ansioso di andarsene che era pronto ad accettare un posto inferiore a Parma, in un'università che non aveva il corso di matematica. Mario Pieri, però, che era stato uno dei maestri di Levi a Torino, era a Parma e desiderava che il suo ex allievo lo raggiungesse lì. Una volta a Parma (dal 1910), Pieri divenne l'amico più intimo di Levi. Trascorse diciotto anni a Parma impegnandosi notevolmente nello sviluppo scientifico dell'Università con una serie di politiche che produssero ottimi risultati. Levi occupò, oltre alla cattedra di Analisi algebrica, anche quella di Geometria analitica e, per un anno, anche quella di Fisica matematica. Ciò significava che il suo carico di lavoro era estremamente pesante. Tuttavia fece sforzi strenui per far sì che il corso di laurea in matematica si stabilisse a Parma e ottenne l'approvazione del rettore per tale scopo. Purtroppo, lo scoppio della prima guerra mondiale e l'entrata in conflitto dell'Italia nell'aprile 1915, impedirono la realizzazione dei piani di Levi. La guerra vide una tragedia colpire la famiglia Levi, poiché i suoi due fratelli Decio ed Eugenio furono entrambi uccisi in azione nel 1917.

Dopo la fine della guerra, Levi rinnovò i suoi sforzi per ottenere il corso di matematica a Parma. La sua posizione si rafforzò quando divenne presidente della Facoltà di Scienze. Tuttavia, negli anni '20, la situazione politica in Italia cominciò a rendere il suo lavoro sempre più difficile, incidendo seriamente sui suoi tentativi di migliorare lo status di Parma. Giovanni Gentile, professore di storia della filosofia all'Università di Roma nel 1917, divenne ministro dell'istruzione nel governo fascista italiano nel 1922 e nei due anni successivi portò avanti importanti riforme dell’istruzione. Gentile organizzò nel marzo 1925 a Bologna il primo Congresso delle Istituzioni Culturali Fasciste che portò in aprile al "manifesto Gentile" che cercava l'appoggio degli intellettuali al fascismo. Due matematici, Corrado Gini e Salvatore Pincherle, appoggiarono il manifesto mentre altri redassero un contro-manifesto sostenendo l'indipendenza degli intellettuali dalle interferenze politiche. Levi firmò il contromanifesto, così come Leonida Tonelli, Vito Volterra, Guido Castelnuovo, Tullio Levi-Civita e Francesco Severi. Tuttavia, le riforme fasciste continuarono, portando alla chiusura del corso di matematica presso l'Università di Parma. Tutti i matematici se ne andarono tranne Levi, che divenne professore di matematica speciale e preside della scuola di chimica. Nel 1928, però, nell'ambito della riforma fascista venne chiusa anche la scuola di chimica di Parma.

Nonostante queste estreme difficoltà, gli anni di Levi a Parma furono quelli in cui aveva ampliato la già ampia gamma dei suoi campi di ricerca. Prima di recarsi a Parma aveva già pubblicato oltre quaranta articoli su argomenti che spaziavano dalla geometria algebrica alla logica, lavorando in particolare sull'assioma della scelta.

Aveva studiato inoltre la teoria dell'integrazione, le equazioni differenziali alle derivate parziali e il principio di Dirichlet, producendo il "teorema di Beppo Levi", o della convergenza monotona di sequenze di funzioni misurabili, che permette di passare con il limite dentro il segno di integrale quando la successione di funzioni integrate è puntualmente crescente. Il teorema implica in particolare che possiamo calcolare l’integrale di una funzione positiva e misurabile come limite di una successione crescente di integrali di funzioni semplici. Quindi non solo come estremo superiore di integrali di funzioni semplici dominati da f. Data una funzione misurabile positiva, esiste sempre una successione crescente di funzioni semplici che converge a f.

Levi si interessò anche di storia della scienza e di fisica: in quest'ultimo ambito, è da ricordare, in particolare, la sua breve monografia Nuove teorie della meccanica quantistica e le loro relazioni con l'analisi matematica (1926). A questa già ampia gamma di lavori, aggiunse contributi ad argomenti come la teoria dei numeri, l'ingegneria elettrica, la teoria delle misurazioni fisiche e la fisica teorica. Nel 1928 lasciò Parma e passò alla cattedra di teoria delle funzioni dell'Università di Bologna, dove ebbe un oneroso carico didattico e amministrativo, ma continuò a intraprendere la ricerca con le stesse passioni che aveva coltivato per tutta la vita. Scrisse articoli sulla logica, sulle equazioni differenziali, sulle variabili complesse, nonché sul confine tra analisi e fisica. Ebbe anche un ruolo significativo nella Unione Matematica Italiana come redattore del Bollettino dell'Unione Matematica Italiana e direttore dal 1931 al 1938. Per molti versi le cose andarono bene per Levi a Bologna: sua figlia Laura iniziò il dottorato in fisica, ebbe ottimi rapporti con Salvatore Pincherle, allora in pensione ma ancora attivo, e nel 1935 fu eletto alla Reale Accademia dei Lincei.

Nonostante il suo odio per il fascismo, Levi aveva firmato il "giuramento al fascismo" nel 1931 insieme a circa 1200 altri matematici (solo undici si rifiutarono di firmare). Forse anche per questo, per diversi anni poté svolgere le sue funzioni a Bologna con poche interferenze politiche. La situazione cambiò radicalmente nel luglio 1938 quando, sotto la pressione di Hitler, Mussolini presentò il Manifesto della Razza. Questa legge era totalmente antisemita, togliendo la cittadinanza italiana agli ebrei e vietando loro di lavorare nel campo dell’istruzione, del governo e delle banche. Ciò provocò la destituzione di Levi dal suo incarico a Bologna nel 1938. Aveva preso contatti con diversi matematici argentini attraverso il suo lavoro di redattore del Bollettino e, nonostante avesse sessantatré anni, iniziò subito a cercare di negoziare un trasferimento in Argentina. Cortés Plá invitò Levi a dirigere l'istituto di matematica recentemente fondato presso l'Università del Litoral di Rosario. Nell'ottobre del 1939 Levi, con la moglie e le due figlie, lasciò l'Italia ed emigrò in Argentina. In questo periodo emigrò in Palestina il figlio Giulio, che era biologo. Sorprendentemente, sebbene Levi avesse 64 anni quando assunse l'incarico di professore e direttore dell'Istituto di Rosario, poté continuare a insegnare, intraprendere ricerche e svolgere compiti amministrativi per altri 20 anni. Oltre a tenere corsi di analisi, geometria e meccanica razionale, fu molto attivo nella ricerca, pubblicando circa un terzo dei suoi lavori in spagnolo. Fondò la rivista Mathematicae Notae, la collana Publicaciones del Instituto de matemáticas e la serie di libri Monografias. Pubblicò “Sistemas de ecuaciones analiticas en terminos finitos, diferenciales y en derivadas parciales" (1944), un’esposizione scritta in modo chiaro dei teoremi fondamentali dell’esistenza dei sistemi di equazioni differenziali alle derivate parziali analitiche, insieme al necessario materiale preliminare sulle funzioni implicite e sulle equazioni differenziali ordinarie.

Nel 1947 Levi pubblicò “Leyendo a Euclides” (Leggere Euclide).LM Blumenthal scrive in una recensione:

“Questo simpatico libricino registra in modo informale alcuni pensieri di un matematico scaturiti dalla lettura degli 'Elementi' di Euclide. Sebbene l’autore neghi qualsiasi intenzione di scrivere uno studio storico serio o una critica moderna di Euclide, nel libro c’è molto di entrambi”

Nel 1956 Levi ricevette il Premio Antonio Feltrinelli dell'Accademia dei Lincei.

A Levi era stata offerta la possibilità di tornare alla sua cattedra a Bologna dopo la fine della seconda guerra mondiale, ma scelse di restare in Argentina. Levi e sua moglie Albina fecero molte visite in Italia dopo essere emigrati in Argentina, e fu in Italia che Albina morì nel 1951. Morì a Rosario all'età di 86 anni e lì fu sepolto nel cimitero ebraico.

Il solitario Barricelli e la nascita degli organismi numerici

 

Il MANIAC (acronimo di Mathematical Analyzer, Numerical Integrator And Computer), la cui architettura fu progettata quasi esclusivamente da John von Neumann agli inizi degli anni Cinquanta, era il più potente “cervello elettronico” dell’epoca e fu installato presso l’IAS (Institute for Advanced Study) di Princeton, nel New Jersey. Finanziato quasi interamente con fondi delle forze armate, serviva principalmente per eseguire i complessi calcoli che portarono alla costruzione della bomba termonucleare all’idrogeno. Il suo nome, scherzoso e non ufficiale, faceva il verso a quello dell’ENIAC, che lo aveva preceduto dal 1946, sempre con scopi principalmente militari (e per le previsioni meteorologiche). C'erano cinque kilobyte di memoria totale archiviati nella macchina. Un’inezia per gli standard odierni, ma allora era un arsenale.

Maniac è il nome anche della bella e documentata biografia romanzata di John von Neumann e storia dell’evoluzione del suo calcolatore elettronico, scritta dal cileno Benjamín Labatut (Adelphi, 2023). Di sicuro Labatut ha giocato con il significato della parola che, in inglese come in italiano, indica una persona con problemi mentali, un pazzo. E il libro abbonda di figure di persone geniali e un po’ folli, a cominciare dallo stesso matematico di origine ungherese. Ma von Neumann non è il solo. A metà circa di Maniac compare e scompare nel giro di due capitoli non consecutivi l’enigmatica e affascinante figura di Nils Aall Barricelli.

Nella finzione letteraria ne parla la testimonianza di Julian Bigelow, l’ingegnere informatico che fu il braccio destro di Von Neumann nella progettazione e nella realizzazione della macchina. Il capitolo si intitola proprio “Un vero scienziato pazzo”.

Appena il MANIAC cominciò a funzionare Johnny chiamò a lavorarci un vero scienziato pazzo. 

Nils Aall Barricelli. 

Mezzo norvegese e mezzo italiano. 

Totalmente folle.

A Johnny era venuta un'ossessione per la biologia, e quest'uomo lasciò nel suo ufficio un bigliettino scritto a mano. 

“Interessato a condurre una serie di esperimenti numerici allo scopo di verificare la possibilità che un'evoluzione simile a quella degli organismi viventi abbia luogo in un universo creato artificialmente”. 

Con accluse specifiche e alcune pubblicazioni accademiche. 

Johnny mi chiese cosa ne pensavo. 

Non aspettò la mia risposta. 

L'indomani gli accordò libero accesso. 

Gli disse che poteva far girare qualunque simulazione volesse. 

Una volta terminati i calcoli per la bomba, ovviamente.

Barricelli era nato a Roma il 24 gennaio 1912 da padre italiano e madre norvegese. Secondo Richard Goodman, un microbiologo che fece amicizia con il matematico negli anni '60, Barricelli affermava di aver inventato il calcolo infinitesimale prima del suo decimo compleanno. Quando il ragazzo mostrò i calcoli a suo padre, apprese che Newton e Leibniz lo avevano preceduto di un paio di secoli. Mentre era studente all'Università di Roma, Barricelli studiò matematica e fisica con Enrico Fermi. Un paio d'anni dopo la laurea nel 1936, emigrò in Norvegia con la madre recentemente divorziata e la sorella minore.

Mentre infuriava la Seconda guerra mondiale, Barricelli studiava. Nonostante avesse presentato una tesi di 500 pagine sull'analisi statistica delle variazioni climatiche nel 1946, Barricelli non completò mai il suo dottorato di ricerca. La commissione di tesi gli ordinò di ridurre l’articolo a un decimo delle dimensioni, altrimenti non avrebbe accettato il lavoro. Invece di capitolare, Barricelli rinunciò alla laurea.

Barricelli iniziò a modellare i fenomeni biologici su carta, ma i suoi calcoli erano lenti e limitati. Fece domanda per studiare negli Stati Uniti come borsista Fulbright, dove avrebbe potuto lavorare con la macchina IAS. Come scrisse nella sua richiesta di borsa di studio originale nel 1951, cercò di “effettuare esperimenti numerici per mezzo di grandi macchine calcolatrici”, al fine di chiarire, attraverso la matematica, “i primi stadi dell’evoluzione di una specie”. Desiderava anche socializzare con grandi menti: “comunicare con statistici e teorici dell’evoluzione americani”. Al momento della presentazione della domanda era un assistente di 39 anni presso l'Università di Oslo.

Sebbene il programma inizialmente lo respinse a causa di un problema di visto, all'inizio del 1953 Barricelli arrivò all’Institute for Advanced Study come membro in visita. "Spero che troverete il signor Baricelli [sic] una persona interessante con cui parlare", scrisse Ragnar Frisch, un collega di Barricelli che più tardi avrebbe vinto il primo Premio Nobel per l'economia, in una lettera a von Neumann. “Non è sempre molto sistematico nella sua esposizione”, continuava Frisch, “ma ha idee interessanti”. Comunque, non è vero che “fu chiamato”, ma fu presentato con ottime credenziali.

Le sue idee erano deliranti. 

Voleva imitare all'interno del MANIAC l’evoluzione della vita.

“Il primo linguaggio e la prima tecnologia sulla Terra non furono creati da esseri umani. Furono creati da molecole primordiali quasi quattro miliardi di anni fa. Sto pensando alla possibilità che un processo evolutivo potenzialmente in grado di condurre a risultati analoghi si possa avviare nella memoria di un calcolatore”.

Credeva nella simbiogenesi. 

Una teoria estremamente controversa opposta al darwinismo. 

Spiega la complessità degli organismi viventi attraverso le associazioni simbiotiche anziché mediante la selezione naturale dell'ereditarietà. 

Una fusione tra forme più semplici.

L'ipotesi simbiogenetica fu articolata per la prima volta dal naturalista russo Konstantin Merezhkovsky nel 1905. Egli era già a conoscenza del lavoro svolto dal botanico tedesco Andreas Schimper, che, avendo osservato nel 1883 come la divisione dei cloroplasti nelle piante verdi ricordasse quella dei cianobatteri, aveva proposto che le piante verdi derivino dall'unione simbiotica di due organismi. Successivamente, nel 1920, Ivan Wallin estese l'idea di un'origine endosimbiontica anche ai mitocondri. Ma tutte queste ipotesi furono inizialmente tralasciate o confutate. Analisi più dettagliate di cianobatteri e cloroplasti, effettuate grazie al microscopio elettronico, e la scoperta che i plastidi e i mitocondri contengono un proprio DNA (che fu riconosciuto come il materiale ereditario degli organismi) portarono a una rivalutazione dei fatti negli anni Sessanta.

Come avrebbe scritto lo stesso Barricelli in un lungo articolo riguardante il suo lavoro su Civiltà delle macchine di Leonardo Sinisgalli (1955: a. 3, mag., fasc. 3, pp. 27-33), “Un'ipotesi ardita fu avanzata nel 1924 da Kozo-Polyansky quando già si cominciava a sapere qualche cosa di queste analogie. L'ipotesi di Kozo-Poliansky è che tutti i geni ed anche diverse altre molecole della cellula che sono dotate di potere autocatalitico discendono da altrettanti virus od organismi di natura simile ai virus che per simbiosi un po’ per volta si sono associati al resto della cellula. Secondo questa teoria, che Kozo-Polyansky chiama teoria della “simbiogenesi“, il processo di evoluzione che ha permesso la formazione della cellula fu iniziato da una simbiosi tra alcuni organismi di natura simile ai virus. A questi poi col tempo si sarebbero associati nuovi simbionti della stessa natura ed in numero sempre crescente, ed il processo di evoluzione così iniziato avrebbe reso possibile la formazione dei vari organi della cellula”. 

Sul registro del computer di Barricelli presso l’Institute for Advanced Study, in caratteri scritti a mano a matita datati 3 marzo 1953, c’è il titolo “Problema di simbiogenesi”.

La teoria della simbiogenesi nella sua moderna accezione fu esposta e diffusa per la prima volta nel 1975 da Lynn Margulis, che la ufficializzò nel 1981 nel libro Symbiosis in Cell Evolution (La simbiosi nell'evoluzione cellulare); nel libro viene spiegato come le cellule eucariotiche si siano originate come comunità di entità interagenti tra loro, tra cui ad esempio spirochete endosimbiontiche che svilupparono flagelli e ciglia eucariotici, ma la biologa andrebbe, con più ragione, ricordata per la sua opera di divulgatrice. Infatti, alle spalle dell’opera di Lynn Margulis c’è una lunga storia di idee, alle quali è molto debitrice (e stranamente non cita l’articolo di Kozo-Polyansky che Barricelli conosceva bene).

Attualmente la simbiogenesi è largamente accettata e supportata da prove scientifiche. Nei primi tempi venne accettata molto lentamente tra i biologi, ma grazie al largo numero di prove portate a sostegno nei 30 anni seguenti, è utilizzata su un numero sempre maggiore di sistemi biologici. Oggi è l'unica spiegazione plausibile esistente per l'evoluzione e la discontinuità esistente tra procarioti ed eucarioti.

Disseminò di numeri casuali la memoria del MANIAC.  

Introdusse regole per governare il loro comportamento. 

È così che li faceva “evolvere”. 

La sua ipotesi era che avrebbero cominciato a mostrare le stesse caratteristiche dei geni.

(...)

Ognuno degli organismi di Barricelli era una stringa di numeri. 

Entravano in contatto si fondevano mutavano morivano o procreavano. 

Potevano instaurare una simbiosi per diventare più complessi. 

Potevano regredire a forme piü semplici. 

Trasformarsi in predatori. In parassiti.

Barricelli codificò i suoi organismi numerici sulla macchina IAS per dimostrare la sua tesi. Scrisse che "È molto facile fabbricare o semplicemente definire entità con la capacità di riprodursi, ad esempio, nel regno dell'aritmetica".

Ma qual era il metodo che utilizzava? Lo spiega nell’articolo su Civiltà delle macchine:

“Per esempio, possiamo usare come elementi alcuni numeri scritti sulla prima linea di un foglio a quadretti - vedi fig. 1 dove i numeri negativi sono sottolineati - e scegliere ad arbitrio una regola di riproduzione di questi numeri.

In fig. 1 si è usata la seguente: in una unità di tempo (generazione) un numero positivo m si riproduce m caselle a destra ed un numero negativo n si riproduce n caselle a sinistra. Il risultato che si ottiene dalla prima riga seguendo questa regola di riproduzione è scritto nella seconda riga. Applicando la stessa regola di riproduzione sulla seconda riga si ottiene la terza riga, e così via. Naturalmente per continuare bisognerà fissare delle regole per fissare ciò che dovrà avvenire quando due numeri capitano nella stessa casella. Ma di ciò si parlerà più avanti.

L’altra facoltà essenziale per una evoluzione darwiniana, la capacità di subire cambiamenti ereditari, non è così diffusa come la capacità di riprodursi, ma si conoscono elementi in cui la detta capacità esiste (...) Artificialmente non vi è alcuna difficoltà a definire elementi che oltre alla facoltà di riprodursi hanno anche la facoltà di subire cambiamenti ereditari. Negli elementi numerici sopra definiti possiamo per esempio stabilire delle regole di mutazione approfittando dei casi in cui due numeri capitano nella stessa casella. Il numero da collocare nella detta casella potrà risultare diverso da entrambi e rappresenterà in tal caso una mutazione. (...)

In questo modo si ha una classe di elementi numerici capaci di riprodursi è di subire mutazioni. Le condizioni per un processo di evoluzione in base ai principi di Darwin sarebbero presenti. I numeri, che hanno maggiore probabilità di sopravvivere nell’ambiente creato dalle regole che abbiamo scelto, sopravviveranno. Gli altri verranno man mano eliminati. Si avrà un processo di adattamento all’ambiente, un processo di evoluzione darwiniana”.

Poi, per indurre processi di evoluzione, cambiava le regole: “Per mettere alla prova la teoria della simbiosi dei geni possiamo ricorrere ancora una volta all’impiego di elementi numerici. Basterà modificare le regole della riproduzione impiegate in maniera tale da favorire qualche forma di associazione utilitaria (simbiosi) tra elementi numerici diversi. Così si potrà vedere se è vero che associando elementi con le proprietà fondamentali precedentemente descritte si possa iniziare un processo di evoluzione che si svolga in base allo stesso meccanismo che regola l’evoluzione biologica. Per favorire l’associazione utilitaria (simbiosi) possiamo apportare alle regole di riproduzione adottate delle modifiche per (...) rendere possibile la riproduzione di un elemento numerico solo quando ne sono presenti degli altri da esso differenti. In tal modo si rende necessaria l'associazione utilitaria (simbiosi) di elementi numerici diversi onde rendere possibile la riproduzione. Alle suddette regole di riproduzione si possono poi associare delle regole di mutazione a piacere, per es. sfruttando i casi in cui due numeri cadono nella stessa casella”.

E così via, fino alla prova di compilare la prima riga (generazione) di soli 1 e -1 e caselle vuote (0) estraendoli a sorte in modo casuale con il lancio di due monete.

Il bello è che, all’inizio, faceva tutto con penna e fogli quadrettati. Solo successivamente ebbe la possibilità di ricorrere alla schede perforate del computer.

All'interno del dispositivo, Barricelli programmò mondi costantemente mutabili, ciascuno con file di 512 "geni", rappresentati da numeri interi relativi. Mentre il computer attraversava centinaia e migliaia di generazioni (il massimo fu 5.400) emergevano raggruppamenti persistenti di geni, che Barricelli considerava organismi. Il trucco consisteva nel modificare le leggi della natura create dall’uomo - “norme”, come le chiamava lui - che governavano l’universo e le sue entità. Doveva mantenere questi ecosistemi sull’orlo del disordine e della stasi. Troppo caos e le sue creature si sarebbero trasformate in un caos disorganizzato; troppo poco e si sarebbero omogeneizzate. Il punto nel mezzo, tuttavia, sosteneva processi realistici.

L’azione di equilibrio di Barricelli non era sempre facile. Le sue prime prove furono piene di parassiti: geni numerici primitivi, spesso singoli, invasero lo spazio e divorarono i loro vicini. In genere, era in grado di assistere solo a un paio di cambiamenti ereditari, o al massimo a una manciata, prima che il mondo si distruggesse. Per creare processi evolutivi duraturi, aveva bisogno di ostacolare la capacità di questi parassiti di riprodursi rapidamente. Quando tornò all'Istituto nel 1954 per iniziare una seconda serie di esperimenti, Barricelli apportò alcuni cambiamenti cruciali. Innanzitutto, limitò la proliferazione dei parassiti a una volta per generazione. Questo vincolo consentiva ai suoi organismi numerici un più ampio margine di manovra per superare il problema. In secondo luogo, iniziò a impiegare norme diverse per le diverse sezioni dei suoi universi. Ciò costringeva i suoi organismi numerici ad adattarsi sempre.

Anche negli universi precedenti, Barricelli si rese conto che la mutazione e la selezione naturale da sole non erano sufficienti a spiegare la genesi delle specie. In effetti, la maggior parte delle singole mutazioni erano dannose. Scrisse che “La maggior parte delle nuove varietà che hanno mostrato la capacità di espandersi sono il risultato di fenomeni di incrocio e non di mutazioni, sebbene le mutazioni (soprattutto quelle dannose) siano state molto più frequenti dei cambiamenti ereditari mediante incrocio negli esperimenti condotti".

Quando un organismo diventava perfettamente adatto ad un ambiente, la più piccola variazione non faceva altro che indebolirlo. In tali casi, furono necessarie altre modificazioni, effettuate mediante una fecondazione incrociata, per dare all'organismo numerico una qualche possibilità di miglioramento. Ciò indicava a Barricelli che le simbiosi, l’incrocio genetico e “una forma primitiva di riproduzione sessuale” erano essenziali per l’emergere della vita.

Barricelli programmò alcuni dei primi algoritmi informatici che assomigliano ai processi della vita reale: una suddivisione di ciò che oggi chiamiamo “vita artificiale”, che cerca di simulare i sistemi viventi nei computer. Barricelli lanciò una sfida coraggiosa al modello darwiniano standard di evoluzione per competizione, dimostrando che gli organismi si sono evoluti anche per simbiosi e cooperazione.

In effetti, i progetti di Barricelli hanno anticipato molte attuali vie di ricerca, compresi gli automi cellulari, programmi per computer che coinvolgono griglie di numeri abbinate a regole locali che possono produrre comportamenti complicati e imprevedibili. I suoi modelli hanno una sorprendente somiglianza con gli automi cellulari unidimensionali (reticoli realistici di schemi numerici) proposti da Stanislaw Ulam e, manco a dirlo, da von Neumann, e studiati da Stephen Wolfram.

Barricelli vedeva i suoi organismi informatici come un modello di vita, su questo pianeta e su qualsiasi altro. "La questione se un tipo di simbioorganismo si sviluppi nella memoria di un computer digitale mentre un altro tipo si sviluppi in un laboratorio chimico o mediante un processo naturale su qualche pianeta o satellite non aggiunge nulla di fondamentale a questa differenza", scrisse. Un mese dopo che Barricelli aveva iniziato i suoi esperimenti sulla macchina IAS, Crick e Watson annunciarono la forma del DNA come una doppia elica. Ma conoscere la forma della vita biologica non ha intaccato la convinzione di Barricelli di aver catturato i meccanismi della vita su un computer. Lasciamo che Watson e Crick definiscano il DNA una doppia elica. Barricelli li chiamava “numeri a forma di molecola”.

Ogni due cicli prendeva un campione dalla memoria del MANIAC e lo stampava.

Rigogliosi paesaggi matematici simili a giganteschi quadri espressionisti astratti.

L'elettroencefalogramma di un folle. 

Fissava un punto e gridava Perfetto! quando gli organismi si erano scambiati dei "geni" per creare un simbionte. 

Scandaloso! quando diventavano parassiti.

Gli esperimenti di Barricelli avevano anche un lato estetico. Insolitamente per l’epoca, convertì gli 1 e gli 0 digitali della memoria del computer in immagini pittoriche per evidenziare i suoi organismi numerici Quelle immagini, e le idee alla loro base, avrebbero influenzato gli animatori computerizzati nelle generazioni a venire.

Barricelli non si è limitato a creare un universo di organismi numerici, ha convertito i suoi organismi in immagini. I conteggi computerizzati di 1 e 0 si sarebbero poi auto-organizzati in griglie visive di squisita varietà e consistenza.

Barricelli era convinto che i numeri potessero cominciare a sviluppare una vita propria.

Sono l'inizio di una qualche forma di vita aliena o semplicemente modelli della vita? No, non sono modelli. Sono una particolare categoria di strutture autoreplicanti, già definite!

“Ma deve essere ben chiaro che il compito delle nostre ricerche non è stato quello di indagare come si siano svolte le prime fasi dell’evoluzione biologica. Il nostro compito è invece di indagare se processi di evoluzione in base agli stessi principi che, come si suppone, regolano l’evoluzione biologica sono possibili e come si svolgerebbero inizialmente partendo da elementi numerici o di qualsiasi natura anche se completamente diversi dai virus e dai geni, purché capaci di riprodursi, di mutare ereditariamente e di associarsi in organizzazioni (simbioorganismi) che offrono un vantaggio selettivo”.

(...)

“Processi di evoluzione secondo i principi dell’evoluzione biologica e i cui i fenomeni di incrocio (o riproduzione sessuale) hanno una parte preponderante, possono essere realizzati con molti tipi di elementi capaci di riprodursi, mutare ed associarsi in simbioorganismi. Non si tratta quindi di un fenomeno particolare caratteristico per un determinati tipo di elementi, come ad esempio le molecole degli acidi desossiribonucleici (virus e geni), ma di un fenomeno statistico generale che interessa molti tipi di elementi con le suddette proprietà”.

(...)

“La possibilità di produrre processi di evoluzione insieme agli stessi principi che regolano l’evoluzione biologica, ma partendo da elementi autoriproduttivi di natura qualsiasi, solleva la questione se gli organismi numerici ed eventualmente altri organismi che possono essere sviluppati in simili processi di evoluzione siano da considerarsi come organismi viventi. Teoricamente siffatti organismi, se sviluppati in universi di dimensioni sufficienti e in condizioni adatte, potrebbero avere le stesse e forse anche maggiori possibilità di evoluzione e varietà di forme. Che si voglia o no riconoscerli come organismi viventi, ciò potrà in definitiva essere una questione di definizione. Volendo scegliere una definizione molto comprensiva si potrebbe considerare come vivente ogni organismo capace di riprodursi e di subire cambiamenti ereditari. Con questa definizione sarebbero viventi non solo i virus e i geni, ma anche gli organismi numerici e gli elementi numerici che li compongono”.

(...)

“Ma anche volendo considerare come viventi soltanto i simbioorganismi di natura, diciamo così, albuminica, non bisogna credere che tutti questi organismi debbano necessariamente rassomigliare alle forme di vita che conosciamo sulla Terra né che la Terra debba essere necessariamente l’ambiente migliore per lo sviluppo di siffatte forme di vita”.

Ma alla fine i suoi esperimenti fallirono. 

Sebbene io abbia creato una classe di numeri capaci di riprodursi e di subire mutamenti ereditari, l’evoluzione numerica non va molto lontano e non ha prodotto in nessun caso un livello di fitness sufficiente a mettere la specie al riparo dalla totale distruzione e ad assicurare un processo evolutivo illimitato come quello che ha avuto luogo sulla Terra e che ha portato a organismi sempre più avanzati. Manca qualcosa che permetta di spiegare la formazione di organi e di facoltà complesse come quelle degli organismi viventi. Per quante mutazioni facciamo, i numeri restano sempre numeri. Non diventeranno mai organismi viventi! 

Appunti presi in preda alla disperazione.

Ciarlatano/visionario? 

Probabilmente entrambe le cose. 

Molto in anticipo sul suo tempo. 

Troppo.

Le sue entità numeriche evolvevano in un universo digitale vuoto nel corso dei pochi cicli di calcolo lasciati liberi dalla bomba all’idrogeno. 

Chissà cosa sarebbe riuscito a ottenere con più cicli a disposizione. 

Ma svanirono senza lasciare tracce. 

Molte delle sue idee furono riscoperte in seguito da altri ricercatori che non erano a conoscenza del suo lavoro.

Fu Johnny a seppellirlo? Forse. 

Fra loro accadde qualcosa. Litigarono di brutto. 

Nessuno dei due ha mai riconosciuto il lavoro dell'altro. 

Nemmeno una parola nei loro scritti. Ho controllato. 

Come se non si fossero mai conosciuti. 

Johnny è ancora riverito come il padre della vita artificiale. 

Mentre l'altro pazzo non lo ricorda nessuno. 

Un giorno di punto in bianco gli fu negato l'accesso al MANIAC. 

Non lo vedemmo mai più.

Ciò che ha sepolto Barricelli nell'oscurità è qualcosa di misterioso. Essere intransigente nelle sue opinioni e non un giocatore di squadra, senza dubbio ha portato all’isolamento di Barricelli dal mainstream accademico. Ma è probabile che Barricelli e l’indomabile von Neumann non andassero più d’accordo.

In un successivo capitolo che Labatut attribuisce alla testimonianza di Barricelli, forse è contenuta la verità sul suo allontanamento da Princeton e dal MANIAC:

“Non sono pazzo. Non sono mai stato pazzo. Non sono folle, anche se molte mi hanno definito così. In tutti questi anni travagliati, questi anni infernali passati a lavorare lontano da tutti, ignorato, vilipeso e invisibile, non ho perso la testa, non ho lasciato che lo sconforto mi conducesse alla follia e mi precipitasse nel delirio. (...) Sono un uomo di scienza. Un sostenitore del potere della verità, un avversario dell'ignoranza e un nemico naturale del nichilismo e dell’incommensurabile abisso della disperazione, perché mi sono votato al futuro. (...) Ma io ho visto qualcosa che mi ha fatto capire che esistono lande selvagge irriducibili alla sola logica, qualcosa che si fa beffe dei venerati principi che gli scienziati hanno tanto a cuore, quel loro cuore debole è pavido - ho visto la vita digitale. Non è in arrivo, è qui. Le creature che ho immaginato si stanno evolvendo più in fretta di quanto potrebbe fare un qualunque sistema biologico. Tanto belle quanto inevitabili. (...) Perciò ho sopportato l’umiliazione di divenire un oggetto di scherno. Uno zimbello. Un esempio negativo, deriso da uomini inferiori sospinti in alto dalle volgari gerarchie del mondo. (...) Ormai è la rabbia a sostenermi (...) Perché è stato a causa della rabbia, del puro rancore cieco che una volta - una volta sola - sono andato vicino a perdere la testa. Ira e sdegno, stizza e odio nei confronti della gazza ladra, di quel demonio sorridente, John von Neumann.

Ha rubato le mie idee! Ha sabotato e usurpato i miei esperimenti, quei numeri scrupolosamente ibridati tra loro che già traboccavano di promesse di vita, e quando non è riuscito a piegarli ai suoi obiettivi li ha distorti e travisati. (...) Usando la sua influenza, ha seppellito la mia ricerca e anche il mio nome, prima negandomi l’accesso al suo calcolatore (il MANIAC, nome quanto mai appropriato), poi evitando deliberatamente qualunque riferimento diretto al mio lavoro in uno dei suoi libri, proprio quello che - per motivi che mi sfuggono - viene considerato da tutti come il compendio definitivo sugli automi e gli organismi digitali. (...) Non ho nemmeno potuto far ricorso: quel bastardo è morto prima di completare il suo libro. (...) Da allora sono rimasto impotente a guardare mentre altri sfruttavano e mietevano un campo che ero stato io il primo a concimare, seminare e far germogliare. (...) Ed è stato allora, quando mi trovavo a un passo dalla scoperta, quando la mia terra promessa cominciava a profilarsi all’orizzonte, che von Neumann ha preso a interessarsi al mio progetto.

All’inizio ne era affascinato quanto me. Arrivava all’istituto nel cuore della notte - l’unico momento in cui mi era concesso lavorare - e mi tempestava di domande molto insistenti. Da quel che sceglieva di chiedere si capiva la qualità del suo pensiero (...) ed ebbi l’opportunità di scrutare dentro la sua testa. Mi chiese se avessi sentito parlare delle macchine di Turing con oracolo. Col tempo sono giunto a considerare quella semplice domanda come un test (...) Turing anelava a qualcosa di diverso [dai calcolatori moderni], una macchina capace di guardare oltre la logica e comportarsi in modo più simile agli esseri umani, che sono dotati non solo di intelligenza, ma anche di intuito. (...)”

Nella sua accezione più ampia, un oracolo può essere considerato come una serie di procedure di decisione in grado di superare i limiti di una Macchina di Turing, In pratica, l’accesso all’oracolo renderebbe una macchina ibrida capace di affrontare classi di problemi che nessun sistema algoritmico può risolvere. Un altro campo in cui gli oracoli hanno mostrato una funzione teorica è nella classificazione dei problemi “trattabili” o “intrattabili”, risolvibili cioè in tempo polinomiale o esponenziale in relazione alla dimensione n del problema. Ovviamente, il potere di calcolo di una macchina di Turing con oracolo è conseguenza diretta delle caratteristiche di decidibilità del linguaggio oracolo. Una macchina di Turing con oracolo è tale se, di fronte a un problema computazionale incalcolabile, almeno in certo tempo, in cui è necessaria una scelta (sì o no), tira a indovinare, esattamente come facciamo noi.

“Non dimenticherò mai quel momento. (...) Ero arrivato all’istituto a mezzanotte e stavo scendendo le scale che conducevano al MANIAC, quando (...) mi accorsi subito, con mio estremo sconcerto, che il MANIAC stava lavorando a pieno regime, e che von Neumann stava facendo girare il mio codice. Il mio codice!” (...) Lui mi assecondò è non parve risentirsi per il mio tono, ma quando notai che aveva ottimizzato diverse subroutine e introdotto importanti cambiamenti nei miei successivi cicli computazionali, alterando le mie istruzioni in modi che non riuscivo a comprendere, persi il controllo. Mi sentii a tal punto tradito che lo spinsi via è balzai in avanti per interrompere il processo prima che fosse troppo tardi. (...)

Non riesco a ricordare cosa dissi a quel mostro per allontanarlo dal mio esperimento, ma ricordo con assoluta chiarezza che lui reagì in modo sorprendentemente pacato. (...) Fece orecchie da mercante alle mie lamentele e si limitò ad andarsene senza proferire parola, e senza scusarsi per quel che aveva fatto. Né mai si sarebbe scusato in futuro. Quella fu l’ultima volta in cui ci parlammo, e capii subito che i miei giorni col MANIAC erano contati”.

Insomma, mentre Barricelli voleva ricreare la vita in un ambiente digitale, von Neumann voleva creare l’intelligenza artificiale. In più era molto più potente, e non certo uno stinco di santo.

Barricelli morì a Oslo nel 1993, solo e dimenticato.