Metanogenesi e riscaldamento globale

 

La metanogenesi (produzione di metano) è un'antica via metabolica svolta esclusivamente da un gruppo di Archaea (archeobatteri) anaerobici noti come metanogeni. Gli studi geologici suggeriscono che i metanogeni si sono evoluti più di 2,5 miliardi di anni fa, prima che l'ossigeno diventasse abbondante nell'atmosfera terrestre. I metanogeni sono onnipresenti nei suoli, anche in ambienti desertici asciutti. Tuttavia, la loro attività, che produce poca energia, è limitata ad ambienti a bassa ossidoriduzione creati dall'esaurimento degli accettori di elettroni più energeticamente favorevoli. 

I tassi di produzione di metano nel suolo sono più alti quando i suoli sono saturi (poiché l'ossigeno si diffonde 10.000 volte più lentamente nell'acqua rispetto all'aria) o ricchi di materia organica labile che può alimentare la domanda biologica di ossigeno dalla respirazione eterotrofica. Ciò porta a condizioni anossiche e alle condizioni redox basse necessarie per la metanogenesi. Pertanto, a scala di ecosistema, la presenza persistente e la profondità della falda freatica controllano il volume del suolo in cui può verificarsi la produzione di metano. Tuttavia, anche in un suolo insaturo o povero di sostanza organica, le condizioni anossiche possono svilupparsi su una scala molto piccola (μm) in cui vivono i metanogeni. Questo spiega come la produzione di metano possa avvenire in suoli ricchi di ossigeno con un potenziale redox alto, anche se a tassi inferiori rispetto ai suoli anossici. 

La produzione di metano è sensibile a una serie complessa di fasi di decomposizione anaerobica, anche se i metanogeni stessi utilizzano solo il più semplice dei substrati. I substrati per la produzione di metano includono H₂/CO₂ (idrogenotrofico), in cui H₂, formiato, alcol o CO sono usati come donatori di elettroni, cioè come riducenti; acetato (acetoclastico), dove viene ridotto il gruppo metile dell’acetato; e, più raramente, composti metilati (metilotrofici), in cui i metanogeni riducono anche il gruppo metilico da metanolo, dimetilsolfuro, mono-, di- e trimetilammine. I metanogeni nel suolo producono metano attraverso due vie principali: 

Sia l'acetato che l'idrogeno sono sottoprodotti della fermentazione anaerobica; quindi, la metanogenesi dipende da una catena alimentare complessa. La maggior parte dei detriti vegetali è costituita da polimeri scarsamente solubili, come cellulosa, lignina, lipidi e proteine. Questo materiale deve essere prima scomposto in unità solubili o monomeri, di solito da enzimi extracellulari, prima che possa essere metabolizzato dai microbi del suolo. I monomeri devono quindi essere fatti fermentare per produrre i substrati metanogenici, principalmente idrogeno e acetato. Le radici delle piante rilasciano anche composti di carbonio che i microbi possono decomporre anaerobicamente per produrre acetato. La produzione di metano dipende quindi dalla decomposizione anaerobica e dalla fermentazione per fornire i substrati, piuttosto che direttamente dalla quantità o dalla qualità della materia organica.

L'energetica della metanogenesi idrogenotrofica sembra in teoria essere relativamente favorevole, ma, in pratica, i tassi di crescita e le rese cellulari sono inferiori a quanto previsto da considerazioni termodinamiche. Ciò è in parte dovuto al fatto che la crescita autotrofica richiede l'uso di parte del substrato per l'assimilazione del C, inclusa una quantità significativa di ATP. L'energia della metanogenesi acetoclastica è meno favorevole di quella della metanogenesi idrogenotrofica, risultando in tassi di crescita ancora più lenti e rese cellulari inferiori. In generale, è stato anche riportato che l'aumento della salinità inibisce i metanogeni idrogenotrofici, ma migliora la metanogenesi acetoclastica.

In presenza di ioni nitrato o ioni solfato, i metanogeni sono superati dai batteri che respirano più accettori di elettroni che producono energia. Ad esempio, i riduttori di Fe(III) interferiscono con il metabolismo dei metanogeni competendo per il carbonio organico e sopprimono la metanogenesi poiché la riduzione di ferro produce più energia libera rispetto alla metanogenesi. Anche i batteri riduttori di solfato sono un gruppo che interagisce strettamente con i metanogeni nelle sacche anaerobiche dei sedimenti. L'interazione è competitiva per i substrati, e dipende dalla presenza di solfato e salinità dell'ambiente. La metanogenesi è influenzata da vari fattori ambientali e favorita da condizioni fortemente riduttive. Tuttavia, negli habitat anaerobici impoveriti di solfato, in particolare nei sedimenti d'acqua dolce e, a una certa profondità, nei sedimenti marini, i metanogeni svolgono un ruolo centrale come scavenger (spazzini) di H₂ e nella mineralizzazione terminale dell'acetato. In quanto tali, contribuiscono in modo significativo al ciclo del carbonio. 

La metanogenesi eseguita dagli Archaea anaerobici rappresenta la più grande fonte biogenica di metano sulla Terra. Questo processo è una componente chiave del ciclo globale del carbonio e svolge un ruolo importante nei cambiamenti climatici, a causa dell'alto potenziale di riscaldamento del metano. 

I previsti aumenti della temperatura e le variazioni delle precipitazioni dovute al cambiamento climatico altereranno la produzione di metano nel suolo, il che potrebbe avere effetti di feedback sul cambiamento climatico. Tuttavia, questi feedback sono difficili da prevedere. I tassi di metanogenesi aumenteranno a temperature più elevate, come è generalmente vero per i processi microbici del suolo, ma l'entità dell'aumento è incerta. I climi più caldi potrebbero portare a stagioni di crescita più lunghe, aumentando la produttività delle piante e quindi maggiori emissioni di metano dovute all'aumento dell'apporto di materia organica. Inoltre, poiché la produzione di metano richiede condizioni anossiche, i cambiamenti nei modelli di precipitazione che alterano l'estensione della terra allagata cambierebbero notevolmente le emissioni di metano del suolo. L'essiccazione del suolo a causa della riduzione delle precipitazioni rallenterebbe la produzione di metano e aumenterebbe l'ossidazione aerobica del metano, riducendo così le emissioni. L'aumento dell'intensità e della frequenza delle precipitazioni già verificatesi in alcune regioni del mondo potrebbe invece aumentare l'estensione delle zone umide, aumentando così le emissioni globali di metano nell'atmosfera. 

Con lo scioglimento del permafrost (il suolo perennemente ghiacciato), anche l'estensione delle zone umide e la produzione di metano possono aumentare. Negli ultimi anni, gli scienziati del clima hanno avvertito che lo scongelamento del permafrost in Siberia e in Canada potrebbe essere una "bomba a orologeria a metano" che esplode lentamente. Il riscaldamento delle temperature nelle regioni artiche sta rilasciando enormi quantità di metano, solo parzialmente prodotto da metanogenesi recente in zone diventate umide, ma soprattutto quello fossile intrappolato negli antichi calcari. Oggi questi giacimenti metaniferi sono naturalmente sigillati verso l'alto dalle vaste estensioni di terreni congelati, impermeabili quindi ai gas. Nel territorio artico dell'emisfero boreale (dove sono la maggior parte di terre emerse del pianeta, e quindi esposte al congelamento e scongelamento), si teme la liberazione di grandi quantità di metano nell'atmosfera terrestre, che si aggiungerebbe agli altri gas che già favoriscono l'effetto serra, innescando così, in un circolo vizioso, un ulteriore aumento delle temperature medie terrestri.

Attacco allo spettro di Sheldon

 

Il 19 novembre 1969, la nave di ricerca Hudson salpò dalle gelide acque del porto di Halifax in Nuova Scozia e si inoltrò in mare aperto. La nave iniziava ciò che molti scienziati marini a bordo consideravano l'ultimo grande viaggio di esplorazione oceanica: la prima circumnavigazione completa delle Americhe. La nave era diretta a Rio de Janeiro, dove avrebbe imbarcato altri scienziati prima di attraversare Capo Horn, il punto più meridionale delle Americhe, e poi dirigersi a nord attraverso il Pacifico per attraversare il periglioso Passaggio a Nord-Ovest fino al porto di Halifax, dove tornò il 16 ottobre 1970. 

Lungo la strada, l'Hudson faceva frequenti soste in modo che i ricercatori potessero raccogliere campioni ed effettuare misurazioni. Uno di quegli scienziati, Ray Sheldon, era salito a bordo dell'Hudson a Valparaíso, nel Cile meridionale. Ecologista marino presso il Bedford Institute of Oceanography in Canada, Sheldon era affascinato dal plancton microscopico che sembrava essere ovunque nell'oceano: quanto erano diffusi questi minuscoli organismi? Per scoprirlo, Sheldon e i suoi colleghi raccoglievano e portavano secchi di acqua di mare fino al laboratorio dell'Hudson e utilizzavano un congegno per rilevare le dimensioni e il numero di creature planctoniche. 

La vita nell'oceano, scoprirono, seguiva una semplice regola matematica: l'abbondanza di un organismo è strettamente legata alle dimensioni del suo corpo. Per dirla in altro modo, più piccolo è l'organismo, più ce n’è. Ciò che era più sorprendente fu il modo in cui questa regola sembrava funzionare. Quando Sheldon e i suoi colleghi classificarono i campioni di plancton per ordini di grandezza, scoprirono che ogni intervallo di dimensioni conteneva esattamente la stessa massa di creature. In un secchio di acqua di mare, un terzo della massa del plancton era compreso tra 1 e 10 micrometri, un altro terzo era compreso tra 10 e 100 micrometri e l'ultimo terzo era compreso tra 100 micrometri e 1 millimetro. Ogni volta che scalavano di un intervallo di dimensioni, il numero di individui in quel gruppo diminuiva di un fattore 10. La massa totale rimaneva la stessa, mentre la dimensione delle popolazioni cambiava. Ad esempio, mentre il krill è 12 ordini di grandezza (circa mille miliardi) più piccolo del tonno, è anche 12 ordini di grandezza più abbondante del tonno. Quindi ipoteticamente, tutta la carne di tonno nel mondo sommata (biomassa di tonno) è più o meno la stessa quantità (almeno entro lo stesso ordine di grandezza) di tutta la biomassa di krill nel mondo. 

Sheldon pensava che questa regola potesse governare tutta la vita nell'oceano, dal più piccolo batterio alle più grandi balene. Questa intuizione si è rivelata vera. Lo spettro di Sheldon, come è stato chiamato, è stato osservato anche nel plancton, nei pesci e negli ecosistemi di acqua dolce. (In effetti, uno zoologo russo aveva osservato lo stesso schema nel suolo tre decenni prima di Sheldon, ma la sua scoperta passò per lo più inosservata). 

Lo spettro di Sheldon è una distribuzione a legge di potenza (power law distribution) cioè una relazione del tipo: 

dove µ indica proporzionale, cioè uguale a meno di un fattore moltiplicativo, a (>1) è chiamato esponente della legge di potenza e L(x) è una funzione "che varia lentamente". Quando L(x) è una costante, la distribuzione diventa: 

con C costante di normalizzazione. 

Una distribuzione che obbedisce alla legge di potenza è denominata anche scale-free distribution (distribuzione a invarianza di scala), o anche distribuzione di Pareto. La particolarità di questo tipo di distribuzione sta proprio nell'assenza di una scala caratteristica dei fenomeni. Le leggi di potenza hanno vasta applicazione in biologia, dai modelli di attività neurale ai viaggi alla ricerca di cibo di varie specie. 

Di solito le distribuzioni power-law sono rappresentate su un grafico log-log, cioè un grafico in cui entrambe le variabili sugli assi sono espresse in logaritmi. Trasformando in logaritmi si ha infatti: 

e la relazione diventa lineare. 

Tornando allo spettro di Sheldon, il rapporto rimane approssimativamente lo stesso man mano che ci si sposta più in alto nella catena alimentare. Solo alle estremità estreme dello spettro (i batteri più piccoli e le balene più grandi) le misurazioni hanno iniziato a variare. Un altro modo per comprendere la relazione tra dimensioni e numeri è esaminare il peso dei singoli organismi: 

Biomassa oceanica totale (peso umido) suddivisa in classi dimensionali rilevanti (g, peso umido) per ciascun gruppo per stimare lo spettro dimensionale globale. Ciò è mostrato come il numero totale di individui in ogni classe di grandezza dell'ordine di grandezza sulla piattaforma epipelagica e continentale dell'oceano (superiore a ~ 200 m), dando un esponente di -1,04 (IC 95%: da -1,05 a -1,02). La fascia grigia di confidenza include l'incertezza della biomassa in ciascuna classe dimensionale e l'incertezza nella distribuzione dimensionale di ciascun gruppo. Si noti che gli assi nel grafico sono logaritmici. Come mostra l'equazione nell'angolo in alto a destra, le due grandezze sono legate da una legge che è quasi di proporzionalità inversa. (da Hatton, Heneghan, Bar-On, Galbraith. The global ocean size spectrum from bacteria to whales. Sci Adv. 2021 Nov 12).

Da quando è stato proposto per la prima volta nel 1972, questo modello era stato testato solo all'interno di gruppi limitati di specie in ambienti acquatici, su scale relativamente piccole. Dal plancton marino, ai pesci in acqua dolce, lo schema è rimasto valido: la biomassa delle specie più grandi e meno abbondanti era più o meno equivalente alla biomassa delle specie più piccole ma più abbondanti. 

Ora, l'ecologo Ian Hatton del Max Planck Institute e colleghi hanno cercato di vedere se questa legge riflette anche ciò che sta accadendo su scala globale. Una delle maggiori sfide nel confrontare gli organismi che vanno dai batteri alle balene sono le enormi differenze di scala. I ricercatori hanno stimato gli organismi all'estremità piccola della scala da più di 200.000 campioni d'acqua raccolti a livello globale, ma una vita marina più ampia richiedeva metodi completamente diversi. 

Utilizzando i dati storici, il gruppo ha confermato che lo spettro di Sheldon si adatta a questa relazione a livello globale per le condizioni oceaniche preindustriali (prima del 1850). In 12 gruppi di vita marina, inclusi batteri, alghe, zooplancton, pesci e mammiferi, oltre 33.000 punti della griglia dell'oceano globale, si sono verificate quantità approssimativamente uguali di biomassa in ciascuna categoria di dimensioni dell'organismo. Si è scoperto che ogni classe di dimensioni dell'ordine di grandezza contiene circa 1 gigatonnellata di biomassa a livello globale. 

Hatton e la sua squadra hanno discusso le possibili spiegazioni per questo fatto, comprese le limitazioni imposte da fattori come le interazioni predatore-preda, il metabolismo, i tassi di crescita, la riproduzione e la mortalità. Molti di questi fattori si adattano anche alle dimensioni di un organismo. Ma a questo punto sono tutte speculazioni. Ciò che stupisce è la costanza della regola: perché il rapporto tra numero e dimensioni è questo e non un altro? 

Vi erano tuttavia due eccezioni alla regola, ad entrambi gli estremi della scala dimensionale esaminata. I batteri erano più abbondanti di quanto previsto dalla legge e le balene molto meno. Ancora una volta, il perché è un mistero completo. 

I ricercatori hanno quindi confrontato questi risultati con la stessa analisi applicata ai campioni e ai dati attuali. Sebbene la legge di potenza fosse per lo più ancora verificata, c'era una netta interruzione nello schema, evidente con organismi più grandi. 

"L’impatto umano sembra aver tagliato in modo significativo il terzo superiore dello spettro", ha scritto il gruppo nell’articolo. "Gli esseri umani non hanno semplicemente sostituito i principali predatori dell'oceano, ma hanno invece, attraverso l'impatto cumulativo degli ultimi due secoli, alterato radicalmente il flusso di energia attraverso l'ecosistema". 

Sebbene i pesci rappresentino meno del 3% del consumo annuale di cibo umano, il gruppo ha scoperto che abbiamo ridotto la biomassa di pesci e mammiferi marini del 60% dal 1800. È anche peggio per gli animali più grandi della Terra: la caccia storica ha determinato una riduzione del 90% delle balene.

Questo fatto mette davvero in evidenza l'inefficienza della pesca industriale. Le nostre attuali strategie stanno sprecando molta più biomassa, e l'energia che contiene, di quanta ne consumiamo effettivamente. Inoltre, non abbiamo sostituito il ruolo che una volta svolgeva la biomassa, nonostante ora siamo una delle più grandi specie di vertebrati per biomassa. 

Circa 2,7 gigatonnellate sono state perse dai più grandi gruppi di specie negli oceani, mentre gli esseri umani costituiscono circa 0,4 gigatonnellate. Sono necessari ulteriori ricerche per capire come questa massiccia perdita di biomassa influenzi gli oceani. 

In particolare, la riduzione di grandi animali sembra guidare l'evoluzione di pesci più piccoli o di quelli che diventano sessualmente maturi in giovane età, o entrambi. Molte popolazioni di pesci stanno cambiando drasticamente, con una dimensione media che si riduce del 20% e vite medie più brevi del 25%. Le specie raccolte mostrano i cambiamenti di tratto più bruschi mai osservati nelle popolazioni selvatiche, hanno riferito di recente Michael Kinnison dell'Università del Maine e colleghi. 

Tali cambiamenti sono stati documentati in molti luoghi, tra cui: sardine al largo dell'Africa occidentale; platessa americana al largo di Terranova; salmone atlantico in Canada e Regno Unito; aringhe e temoli al largo della Norvegia; salmone keta in Giappone; sogliola, eglefino e passera di mare nel Mare del Nord; coregone in Alberta; salmone rosso in Alaska; varie specie di salmone nella Columbia Britannica; crostacei in California e merluzzo un po' ovunque. Inoltre, questo lungo elenco include solo i casi in cui sono stati condotti studi rigorosi. È probabile che tali cambiamenti si stiano verificando in ogni popolazione in cui sono presi di mira i pesci di grandi dimensioni. 

Quindi questi cambiamenti sono davvero il risultato dell'evoluzione, o semplicemente una risposta temporanea alle pressioni ambientali? "È molto probabilmente un misto dei due", afferma Kinnison. "L'evoluzione è una componente sostanziale." 

In molti casi, ad esempio, i ricercatori hanno dimostrato che una volta che i pesci raggiungono una certa taglia ed età, è più probabile che diventino prima sessualmente maturi rispetto alle generazioni precedenti. Ciò esclude la maggior parte delle spiegazioni ambientali, come il fatto che i pesci maturano in età precoce perché trovano più cibo e crescono più velocemente. 

Non vi è inoltre alcun dubbio sulla plausibilità di un'evoluzione così rapida. Uno studio decennale sui latterini orientali tenuti in vasche ha dimostrato che un'intensa azione mirata su individui di grandi dimensioni può dimezzare la taglia media in sole quattro generazioni. 

In realtà il tracciamento dei cambiamenti genetici coinvolti non era fattibile fino a poco tempo fa, ma ora è stato fatto per il merluzzo bianco al largo dell'Islanda. I merluzzi con una variante del gene Pan I vivono in acque costiere poco profonde, mentre quelli con un'altra variante vivono in acque più profonde più al largo. Poiché i pescherecci prendono di mira il merluzzo nelle acque costiere poco profonde, la variante poco profonda sta rapidamente diventando meno comune. 

Alcune delle misure di gestione stanno peggiorando le cose. Il merluzzo che vive in profondità si sposta nelle zone costiere poco profonde per deporre le uova, ma queste aree sono chiuse alla pesca durante la deposizione delle uova; quindi, i pesci che vivono in profondità sopportano sempre il peso maggiore della pesca. Nella peggiore delle ipotesi, i pesci poco profondi potrebbero scomparire in 15 anni. Ciò potrebbe portare al collasso della pesca, perché il merluzzo che vive in profondità è molto più difficile, e quindi più costoso, da catturare. 

Esistono altri motivi di preoccupazione, oltre a quello della pesca indiscriminata delle specie più grandi.

La plastica, ad esempio, che galleggia nell'acqua di mare assomiglia molto al cibo per gli uccelli marini (non considerati dalla carta) e per alcune specie di pesci e mammiferi. Le microplastiche hanno effetti ancor più subdoli e deleteri sulle reti alimentari. 

Un altro impatto degli esseri umani sullo spettro di Sheldon è molto meno chiaro, ma il cambiamento climatico antropogenico sta alterando sia la temperatura dell'acqua che la chimica dell'acqua degli oceani. La maggior parte dei microrganismi si è evoluta per un intervallo di temperatura abbastanza ristretto; alterare la temperatura dell'acqua può avere un impatto su di loro. E la CO₂ atmosferica disciolta acidifica l'oceano; con troppa acidificazione, gli organismi dipendenti dalla generazione di carbonato di calcio per gli esoscheletri – molti organismi planctonici e la maggior parte dei molluschi – non possono sopravvivere. Quale sarà l'impatto della scomparsa delle creature marine con esoscheletri?

Qual è l'effetto della distruzione dello spettro di Sheldon? Nessuno lo sa, ma sicuramente non è una buona cosa.

Virus: vivi, non vivi, minaccia, risorsa genetica

 

Si parla in questi difficili anni di come sopprimere il Coronavirus, ma, per molte delle definizioni di vita, i virus non sono esseri viventi. La maggior parte delle numerose definizioni della vita richiede il metabolismo, un insieme di reazioni chimiche che producono energia. Ebbene: i virus non metabolizzano. I virus occupano una posizione tassonomica speciale: non sono piante, animali o batteri procarioti (organismi unicellulari senza nuclei definiti), e sono generalmente collocati nel proprio regno. In effetti, i virus non dovrebbero nemmeno essere considerati organismi, nel senso più stretto, perché non sono a vita libera, cioè non possono riprodursi e portare avanti processi metabolici senza una cellula ospite. Non sono cellule. 

Tutti i veri virus contengono acido nucleico, DNA (acido desossiribonucleico) o RNA (acido ribonucleico), e proteine. L'acido nucleico codifica le informazioni genetiche, uniche per ogni virus. La forma infettiva, extracellulare (fuori dalla cellula) di un virus è chiamata virione. Contiene almeno una proteina sintetizzata da geni specifici nell'acido nucleico di quel virus. In quasi tutti i virus, almeno una di queste proteine ​​forma un guscio (chiamato capside) attorno all'acido nucleico. Alcuni virus hanno anche altre proteine ​​interne al capside; alcune di queste proteine ​​agiscono come enzimi, spesso durante la sintesi degli acidi nucleici virali. I viroidi (che significa "simili ai virus") sono organismi ancor più semplici, che causano malattie che contengono solo acido nucleico e non hanno proteine ​​strutturali. Altre particelle simili a virus chiamate prioni sono composte principalmente da una proteina strettamente complessata con una piccola molecola di acido nucleico. I prioni sono molto resistenti all'inattivazione e sembrano causare malattie degenerative del cervello nei mammiferi, compreso l'uomo (ricordate la “mucca pazza”?).

I virus sono parassiti per antonomasia; dipendono dalla cellula ospite per quasi tutte le loro funzioni vitali. A differenza dei veri organismi, i virus non possono sintetizzare proteine, perché mancano di ribosomi (organelli cellulari) per la traduzione dell'RNA messaggero virale (mRNA; una copia complementare dell'acido nucleico del nucleo che si associa ai ribosomi e dirige la sintesi proteica) in proteine. I virus devono utilizzare i ribosomi delle loro cellule ospiti per tradurre l'mRNA virale in proteine ​​virali.

Essi sono anche parassiti energetici: a differenza delle cellule, non possono generare o immagazzinare energia sotto forma di adenosintrifosfato (ATP). Il virus trae energia, così come tutte le altre funzioni metaboliche, dalla cellula ospite. Il virus invasore utilizza i nucleotidi e gli amminoacidi della cellula ospite per sintetizzare rispettivamente i suoi acidi nucleici e le sue proteine. Alcuni virus utilizzano i lipidi e le catene zuccherine della cellula ospite per formare le loro membrane e le glicoproteine ​​(proteine ​​legate a brevi polimeri costituiti da diversi zuccheri).

La vera parte infettiva di qualsiasi virus è il suo acido nucleico, DNA o RNA, ma mai entrambi. In molti virus, ma non in tutti, l'acido nucleico da solo, privato del suo capside, può infettare le cellule, sebbene in modo considerevolmente meno efficiente dei virioni intatti.

Il capside del virione ha tre funzioni: proteggere l'acido nucleico virale dalla digestione da parte di alcuni enzimi (nucleasi); fornire siti sulla sua superficie che riconoscono e incollano (adsorbimento) il virione ai recettori sulla superficie della cellula ospite e, in alcuni virus, fornire un componente specializzato che consente al virione di penetrare attraverso la membrana della superficie cellulare o, in casi speciali, di iniettare l'acido nucleico infettivo all'interno del cellula ospite. 

Tuttavia, i virus hanno molti tratti degli esseri viventi. Sono fatti degli stessi materiali di costruzione. Si replicano ed evolvono. Una volta all'interno di una cellula, i virus modificano il loro ambiente in base alle loro esigenze, costruendo organelli e dettando quali geni e proteine ​​la cellula produce. È stato scoperto che i virus giganti, che rivaleggiano con le dimensioni di alcuni batteri, contengono geni per le proteine ​​utilizzate nel metabolismo, aumentando la possibilità che alcuni virus possano metabolizzare.

L'etimologia della parola virus si ricollega alla radice indoeuropea vis- che significa essere attivo, essere aggressivo; da questa radice si è sviluppato il latino vīrus = veleno. L'applicazione del termine latino agli agenti infettivi submicroscopici ora considerati virus si deve al microbiologo olandese Martinus Beijerinck nel 1898 a proposito del virus mosaico del tabacco in "Ueber ein Contagium vivum fluidum als Ursache der Fleckenkrankheit der Tabaksblätter", credendo erroneamente che l'agente fosse un fluido (contagium vivum fluidum, "infezione da fluido vivente") perché passava attraverso i filtri in grado di intrappolare i batteri.

Questo virus e quelli successivamente isolati non crescevano su un mezzo artificiale e non erano visibili al microscopio ottico. Nel 1915 e nel 1917, in due studi indipendenti, il britannico Frederick Twort e il franco-canadese Félix d'Hérelle scoprirono lesioni in colture di batteri attribuite a un agente chiamato batteriofago, ora noto per essere un gruppo di virus che infettano specificamente i batteri.

La natura unica di questi agenti richiedeva la necessità di sviluppare nuovi metodi e modelli alternativi per studiarli e classificarli. Lo studio dei virus confinati esclusivamente o in gran parte all'uomo, tuttavia, poneva il grande problema di trovare un ospite animale suscettibile. Nel 1933 i britannici Wilson Smith, Christopher Andrewes e Patrick Laidlaw, dopo aver isolato il virus dell’influenza umana A, furono in grado di trasmettere l'influenza ai furetti e il virus dell'influenza fu successivamente inoculato e studiato nei topi. Nel 1941 l’americano George Hirst scoprì che il virus dell'influenza cresciuto nei tessuti dell'embrione di pollo poteva essere rilevato dalla sua capacità di agglutinare i globuli rossi.

Un progresso significativo fu fatto dagli americani John Enders, Thomas Weller e Frederick Robbins (premi Nobel per la Medicina nel 1954), che nel 1949 avevano sviluppato la tecnica di coltura delle cellule su superfici di vetro; le cellule poterono quindi essere infettate dai virus che causano la poliomielite (poliovirus) e altre malattie (fino a quel momento, il poliovirus poteva essere coltivato solo nel cervello degli scimpanzé o nel midollo spinale delle scimmie). La coltura di cellule su superfici di vetro aprì la strada all'identificazione delle malattie causate dai virus osservando i loro effetti sulle cellule (effetto citopatogeno) e la presenza di loro anticorpi nel sangue. La coltura cellulare portò poi allo sviluppo e alla produzione di vaccini, come il vaccino contro il poliovirus.

I ricercatori furono presto in grado di rilevare il numero di virus dei batteri in un recipiente di coltura misurando la loro capacità di rompere (lisi) i batteri in un'area ricoperta da una sostanza gelatinosa inerte chiamata agar, un’azione virale che provocava un radura, o “placca”. L’italo-americano Renato Dulbecco (Nobel per la medicina nel 1975) nel 1952 applicò questa tecnica per misurare il numero di virus che potevano produrre placche (e quindi anche tumori) in strati di cellule animali adiacenti ricoperte di agar. Negli anni '40 lo sviluppo del microscopio elettronico ha permesso per la prima volta di vedere le singole particelle virali, portando alla classificazione dei virus e fornendo informazioni sulla loro struttura.

I progressi compiuti in chimica, fisica e biologia molecolare dagli anni '60 hanno rivoluzionato lo studio dei virus. Ad esempio, l'elettroforesi su substrati di gel ha fornito una comprensione più profonda della composizione di proteine ​​e acidi nucleici dei virus. Procedure immunologiche più sofisticate, compreso l'uso di anticorpi monoclonali diretti a specifici siti antigenici sulle proteine, hanno fornito una migliore comprensione della struttura e della funzione delle proteine ​​virali. I progressi compiuti nella fisica dei cristalli che possono essere studiati dalla diffrazione dei raggi X hanno fornito l'alta risoluzione necessaria per scoprire la struttura di base dei minuscoli virus. Le applicazioni delle nuove conoscenze sulla biologia cellulare e sulla biochimica hanno aiutato a determinare come i virus utilizzano le cellule ospiti per sintetizzare acidi nucleici virali e proteine.

La rivoluzione avvenuta nel campo della biologia molecolare ha permesso di studiare l'informazione genetica codificata negli acidi nucleici dei virus, che consente ai virus di riprodursi, sintetizzare proteine uniche e alterare le funzioni cellulari. Infatti, la semplicità chimica e fisica dei virus li ha resi un incisivo strumento sperimentale per sondare gli eventi molecolari coinvolti in certi processi vitali. Il loro potenziale significato ecologico è stato compreso all'inizio del nostro secolo, in seguito alla scoperta di virus giganti negli ambienti acquatici in diverse parti del mondo: la complessità genetica dei virus giganti dei fondali oceanici, ad esempio, ha spinto alcuni ricercatori a chiedersi se i virus debbano davvero essere classificati come non viventi. Alcuni di essi possiedono un codice di istruzioni genetiche più grande di quello di alcuni batteri.

La quantità e la disposizione delle proteine ​​e dell'acido nucleico dei virus determinano la loro dimensione e forma. L'acido nucleico e le proteine ​​di ogni classe di virus si assemblano in una struttura chiamata nucleoproteina o nucleocapside. Alcuni virus hanno più di uno strato di proteine ​​che circondano l'acido nucleico; altri ancora hanno una membrana lipoproteica (envelope), derivata dalla membrana della cellula ospite, che circonda il nucleo del nucleocapside. Penetrando nella membrana ci sono proteine ​​aggiuntive che determinano la specificità del virus per le cellule ospiti. I costituenti delle proteine ​​e degli acidi nucleici hanno proprietà uniche per ogni classe di virus; una volta assemblati, determinano la dimensione e la forma del virus per quella classe specifica. I genomi di Mimivirus e Pandoravirus, che sono alcuni dei più grandi virus conosciuti (fino a 1 micron), vanno da 1 a 2,5 Mb (1 Mb = 1.000.000 di paia di basi di DNA).

La maggior parte dei virus varia in diametro da 20 nanometri (nm) a 250-400 nm; i più grandi, tuttavia, misurano circa 500 nm di diametro e sono lunghi circa 700-1.000 nm. Solo i virus più grandi e complessi possono essere visti al microscopio ottico alla massima risoluzione. Qualsiasi determinazione della dimensione di un virus deve anche tener conto della sua forma, poiché diverse classi di virus hanno forme distintive.

Le forme dei virus sono prevalentemente di due tipi: bastoncelli, o filamenti, così chiamati per la disposizione lineare dell'acido nucleico e delle subunità proteiche; e sfere, che sono in realtà poligoni a 20 lati (icosaedri). La maggior parte dei virus delle piante sono piccoli e sono filamenti o poligoni, così come molti virus batterici. I batteriofagi più grandi e complessi, tuttavia, contengono come informazione genetica DNA a doppio filamento e combinano forme sia filamentose che poligonali. Il classico batteriofago T4 è composto da una testa poligonale, che contiene il genoma del DNA e una coda di fibre lunghe a forma di bastoncino con una funzione speciale. Strutture come queste sono esclusive dei batteriofagi.

I virus degli animali mostrano un'estrema variazione di dimensioni e forma. I virus animali più piccoli misurano da circa 20 nm a 30 nm di diametro. Essi possono avere forma di filamenti o poligoni. Alcuni sono lunghi circa 250-400 nm. I virus responsabili di molte malattie infettive sono strutturalmente più complessi e hanno capsidi a forma di bastoncino (elicoidale) oppure poligonale. La maggior parte dei virus con involucro sembra essere sferica, sebbene i rabdovirus siano cilindri allungati. Un coronavirus, ad esempio, possiede un capside sferico in nanoscala formato da un rivestimento lipidico che avvolge i geni, ricoperto di proteine ​​spike, che formano una serie di protuberanze attive biochimicamente.

I criteri utilizzati per classificare i virus in famiglie e generi si basano principalmente su tre considerazioni strutturali: (1) il tipo e le dimensioni del loro acido nucleico, (2) la forma e le dimensioni dei capsidi e (3) la presenza di un involucro lipidico, derivato dalla cellula ospite, che circonda il nucleocapside virale. Mentre i dibattiti sulla classificazione possono a volte sembrare cose da specialisti, in realtà il modo in cui parliamo di virus influisce sul modo in cui vengono ricercati, trattati e, quando serve, combattuti. Infatti, essi non sono solamente “un veleno”.

Rappresentare i virus solo come una minaccia ostacola una reale comprensione dell'evoluzione e della natura. I virus più diffusi sono persistenti e benigni; rimangono dormienti nelle cellule o si riproducono lentamente, senza danneggiare il meccanismo di replicazione di una cellula.

Inoltre, poiché i virus sono spesso classificati come non viventi, molti tipi di infezione virale, specialmente quando i virus colonizzano con successo un ospite in modo persistente e permanente senza causare malattie acute, vengono ignorati come “scienza marginale", e alcuni scienziati considerano le infezioni virali persistenti semplicemente come un fastidio e quindi non urgenti da studiare. 

I virus sono stati ignorati anche in altri modi. Consideriamo l'albero della vita, un modello e uno strumento di ricerca utilizzato per rappresentare l'evoluzione nel tempo. I virus vengono regolarmente esclusi, anche in versioni popolari come l'Albero della vita interattivo. Eppure, senza virus, non si possono comprendere appieno i meccanismi dell'evoluzione.

I virus sono molto abbondanti. Sono diffusi in tutta la vita cellulare, dai batteri unicellulari, all’uomo, agli alberi più maestosi, e sono particolarmente abbondanti nell'oceano, dove agiscono come una gigantesca rete di riciclo, distruggendo ogni giorno il 20 percento dei batteri e altri microbi e rilasciando tonnellate di carbonio, che viene poi utilizzato da altri microrganismi per svilupparsi.

In tutto il mondo, i virus non si limitano a infettare le cellule, ma sono anche fonti di materiale genetico. Il DNA virale viene trasmesso non solo da una particella virale alla sua progenie, ma anche ad altri virus e altre specie. Per questo motivo, le sequenze genetiche virali hanno preso dimora permanentemente nei genomi di tutti gli organismi, compreso il nostro. Il DNA virale è necessario per la formazione della placenta dei mammiferi, è cruciale nella crescita degli embrioni, e il sistema immunitario umano è costituito, in parte, da antiche proteine ​​virali. Quando una persona sta combattendo contro il COVID-19, lo fa con l'aiuto di virus che hanno colonizzato le nostre cellule molto tempo fa.

In effetti, alcuni scienziati considerano i virus la principale fonte di innovazione genetica. I virus non sono un ramo mancante dell'albero della vita. al contrario ne impregnano ogni ramo e foglia. Possiamo sempre chiederci se i virus siano vivi o meno, ma non possiamo contestare la loro importanza per la vita come la conosciamo.

 

I modelli scientifici tra realtà e rappresentazione

 

“Il mondo è una mia rappresentazione»: ecco una verità valida per ogni essere vivente e pensante,

benché l'uomo soltanto possa averne coscienza astratta e riflessa.

E quando l'uomo abbia di fatto tale coscienza, lo spirito filosofico è entrato in lui.

Allora, egli sa con certezza di non conoscere né il sole né la terra, ma soltanto un occhio

che vede un sole, e una mano che sente il contatto d'una terra;

egli sa che il mondo circostante non esiste se non come rappresentazione,

cioè sempre e soltanto in relazione con un altro essere, con il percipiente, con lui medesimo”.

[Arthur Schopenhauer, Il mondo come volontà e rappresentazione,

traduzione di A. Vigliani, Mursia, Milano, 1982]

 

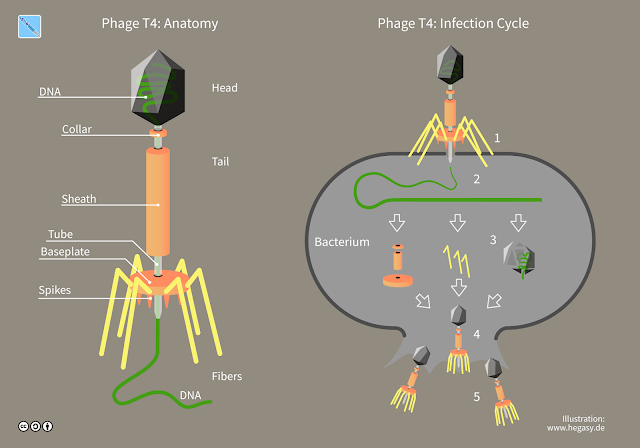
Foto 51

La “Foto 51” è un’immagine a diffrazione dei raggi X di un gel paracristallino composto da fibre di DNA, scattata da Raymond Gosling, uno studente di dottorato che lavorava sotto la supervisione di Rosalind Franklin nel maggio 1952 al King's College di Londra. L'immagine fu etichettata come "foto 51" seguendo l’ordine temporale in cui le foto di diffrazione erano state scattate da Franklin e Gosling. Essa mostra la misteriosa forma a "X" che ispirò James Dewey Watson e Francis Crick a visualizzare la struttura a doppia elica del DNA. Questa straordinaria immagine, la più chiara del DNA mai creata fino a quel momento, fu ottenuta con le tecniche più avanzate allora disponibili. Usando l'immagine di Gosling come prova fisica, Watson e Crick poi pubblicarono la loro idea di struttura teorica del DNA su Nature nel 1953. 

Nel 1962 il Premio Nobel in Fisiologia o Medicina fu assegnato a Watson, Crick e Wilkins. Il premio non fu assegnato a Franklin che era morta quattro anni prima e il comitato per il Nobel non fa nomine postume. Allo stesso modo, il lavoro di Gosling non era citato dal comitato del premio.

La fotografia forniva informazioni fondamentali per lo sviluppo di un modello di DNA. Lo schema di diffrazione consentiva di determinare la natura elicoidale dei fili antiparalleli a doppia elica. L'esterno della catena del DNA ha una spina dorsale di desossiribosio e fosfato alternati mentre le coppie di basi, il cui ordine fornisce i codici per la costruzione delle proteine e quindi l'eredità, sono all'interno dell'elica. I calcoli di Watson e Crick derivanti dalla fotografia di Gosling e Franklin fornirono parametri cruciali per le dimensioni e la struttura dell'elica e la Foto 51 divenne una fonte fondamentale di dati, che portò allo sviluppo del modello del DNA e confermava struttura a doppia elica del DNA ipotizzata in precedenza, presentata in una serie di tre articoli sulla rivista Nature nel 1953.

 

Una fotografia ottenuta con tecniche “non naturali” (i raggi X non li possiamo vedere), quindi già di per sé un modello, aveva consentito la conferma di una teoria basata su altre prove, permettendo la costruzione di un modello di una delle molecole fondamentali della vita. Un modello consentiva un secondo modello che, almeno per allora, sembrava confermare una teoria scientifica. Cosa strana i modelli, belli, utili e difficili da maneggiare.

 

Che cos’è un modello scientifico?

 Un modello scientifico è una rappresentazione fisica, concettuale o matematica di un fenomeno reale difficile da osservare e descrivere direttamente. I modelli creati dagli scienziati devono essere coerenti con le nostre osservazioni, deduzioni e spiegazioni concrete. Tuttavia, i modelli scientifici non sono creati per essere affermazioni fattuali sul mondo, ne sono uno schema: il modello non è la realtà, ma solo una sua rappresentazione semplificata in base alle nostre esigenze di comprensione. 

Lo scopo della modellazione scientifica è molteplice. Alcuni modelli, come il modello tridimensionale a doppia elica del DNA, vengono utilizzati principalmente per visualizzare un oggetto o un sistema, spesso ricavati da dati sperimentali. Altri modelli hanno lo scopo di descrivere un comportamento o un fenomeno astratto o ipotetico. Ad esempio, i modelli predittivi, come quelli impiegati nelle previsioni meteorologiche o nella proiezione degli esiti sanitari delle epidemie, si basano generalmente sulla conoscenza e sui dati di fenomeni del passato e su analisi matematiche di queste informazioni per prevedere e, possibilmente, prevenire futuri, ipotetici eventi di simili fenomeni. I modelli predittivi hanno un valore significativo per la società a causa del loro ruolo potenziale nei sistemi di allarme, come nel caso di terremoti, tsunami, epidemie e simili disastri su larga scala. Tuttavia, poiché nessun singolo modello predittivo può tenere conto di tutte le variabili che possono influenzare un risultato, gli scienziati devono formulare ipotesi sui fattori che possono compromettere l'affidabilità di un modello predittivo e portare a conclusioni errate.

I limiti della modellazione scientifica consistono nel fatto che i modelli generalmente non sono rappresentazioni complete (anche se alcuni pensano che questo sia appunto il loro pregio). Il modello atomico di Bohr, ad esempio, descriveva la struttura degli atomi. Ma, mentre era il primo modello atomico a incorporare la teoria quantistica e fungeva da modello concettuale di base delle orbite degli elettroni, non era una descrizione accurata della natura degli elettroni orbitanti. Né era in grado di prevedere i livelli di energia per gli atomi con più di un elettrone.

Infatti, nel tentativo di comprendere appieno un oggetto o un sistema, sono necessari più modelli, ognuno dei quali rappresenta una parte dell'oggetto o del sistema. Collettivamente i modelli possono essere in grado di fornire una rappresentazione, o almeno una comprensione, più completa dell'oggetto o sistema reale. Ciò è illustrato dal modello ondulatorio e da quello particellare della luce, che insieme descrivono il dualismo onda-particella, in cui la luce possiede natura sia d'onda che di particella. La teoria delle onde e la teoria delle particelle della luce sono state a lungo considerate in contrasto l'una con l'altra. All'inizio del XX secolo, tuttavia, con la scoperta che le particelle si comportano anche come onde, i due modelli furono riconosciuti come complementari, un passo che ha facilitato notevolmente nuove intuizioni nel campo della meccanica quantistica.

Esistono svariati utilizzi della modellazione scientifica. Ad esempio, nelle scienze della Terra, la modellizzazione dei fenomeni atmosferici e oceanici è rilevante non solo per le previsioni meteorologiche, ma anche per la comprensione scientifica del riscaldamento globale. In quest'ultimo caso, un modello oggi importante è il modello di circolazione globale, utilizzato per simulare il cambiamento climatico indotto dall'uomo. La modellizzazione di eventi geologici, come la convezione all'interno della Terra e i movimenti delle placche terrestri, ha fatto progredire le conoscenze di geofisici e geologi su vulcani e terremoti e sull'evoluzione della superficie terrestre. In ecologia, modelli costantemente aggiornati possono essere utilizzati per comprendere le dinamiche delle interazioni tra gli organismi e l’ambiente. Allo stesso modo, vengono utilizzati modelli tridimensionali di proteine ​​per ottenere informazioni sulla loro funzione ​​e per coadiuvare la progettazione di farmaci. La modellazione scientifica ha anche applicazioni nella pianificazione urbana e nella costruzione e nel ripristino degli ecosistemi. Gli scienziati dedicano molto tempo a costruire, calcolare, testare, confrontare e rivedere i modelli; molto spazio sulle pubblicazioni scientifiche è dedicato all'interpretazione e alla discussione delle loro implicazioni.

 

Modelli e rappresentazione

Molti modelli scientifici sono modelli rappresentativi, in quanto rappresentano una parte o un aspetto selezionato del mondo. Esempi standard sono il modello cinetico di un gas che considera le particelle come microscopiche palline in movimento caotico, il modello di Bohr dell'atomo, o il modello in scala di un ponte.

Nella maggior parte dei casi, i modelli non rappresentano il mondo direttamente, ma attraverso sistemi di destinazione (target systems). Essi sono parti della realtà che si studia, e devono essere scelti con attenzione e appropriatezza, specificando anche i criteri di valutazione per ridurre al minimo la frequenza e l'entità degli errori, soprattutto quando si utilizzano modelli per studiare i fenomeni in sistemi complessi del mondo reale. 

A seconda di una serie di fattori molto variabili, si utilizzano diversi tipi di rappresentazione, che giocano un ruolo importante nella pratica della scienza basata sui modelli, vale a dire, per citare i più significativi e meno controversi, modelli in scala, modelli analogici, modelli idealizzati, modelli fenomenologici, modelli esplorativi e modelli di dati. Queste categorie non si escludono a vicenda: un dato modello può rientrare in più categorie contemporaneamente.

Modelli in scala - Alcuni modelli sono copie ridotte o ingrandite dei loro sistemi di destinazione. Un tipico esempio è una piccola automobile di legno o argilla che viene messa in una galleria del vento per esplorare le proprietà aerodinamiche dell'auto reale. Il ragionamento di base è che un modellino in scala sia una replica naturalistica o un'immagine speculare veritiera del sistema reale; per questo motivo, i modelli in scala sono talvolta indicati anche come "veri modelli". Tuttavia, non esiste un modello in scala perfettamente fedele; la fedeltà è sempre limitata ad alcuni aspetti. Il modellino in legno dell'auto fornisce una rappresentazione fedele della forma dell'auto ma non del suo materiale. E anche negli aspetti in cui un modello è una rappresentazione fedele, la relazione tra proprietà del modello e proprietà dell'obiettivo di solito non è banale. Quando gli ingegneri utilizzano, ad esempio, un modello in scala 1:100 di una nave per indagare la resistenza che una nave reale sperimenta quando si muove nell'acqua, non possono semplicemente misurare la resistenza che il modello sperimenta e quindi moltiplicarla per la scala. Infatti, la resistenza affrontata dal modello non si traduce nella resistenza affrontata dalla nave reale in modo semplice (cioè non si può semplicemente scalare la resistenza all'acqua con la scala del modello: la nave reale non deve avere cento volte la resistenza all'acqua del suo modello 1:100). Le due quantità si trovano in una complicata relazione non lineare, e la forma esatta di tale relazione emerge solo come risultato di uno studio approfondito della situazione.

Modelli analogici - Al livello più elementare, due cose sono analoghe se ci sono alcune somiglianze rilevanti tra loro. Un tipo semplice di analogia è quella basata su proprietà condivise. Esiste un'analogia tra la Terra e la Luna basata sul fatto che entrambi sono corpi sferici grandi, solidi, opachi che ricevono calore e luce dal Sole, ruotano attorno ai loro assi e gravitano verso altri corpi. Ma l'uniformità delle proprietà non è una condizione necessaria. Un'analogia tra due oggetti può anche essere basata su somiglianze rilevanti tra le loro proprietà. In questo senso più largo, possiamo dire che c'è un'analogia tra suono e luce perché gli echi sono simili ai riflessi, il volume alla luminosità, il tono al colore, la percettibilità dall'orecchio a quella dall'occhio e così via.

Più recentemente, queste caratteristiche sono state discusse nel contesto dei cosiddetti esperimenti analogici, che promettono di fornire conoscenze su un sistema di destinazione sperimentalmente inaccessibile (ad es. un buco nero) manipolando un altro sistema, il sistema sorgente (ad es. un condensato di Bose–Einstein). Alcuni hanno sostenuto che, date determinate condizioni, una simulazione analogica di un sistema da parte di un altro sistema può confermare le affermazioni sul sistema bersaglio (ad esempio, che i buchi neri emettono radiazioni di Hawking).

Modelli idealizzati - I modelli idealizzati sono modelli che implicano una deliberata semplificazione o distorsione di qualcosa di complicato con l'obiettivo di renderlo più trattabile o comprensibile. Piani privi di attrito, masse puntiformi, sistemi completamente isolati, mercati in perfetto equilibrio sono esempi ben noti. Le idealizzazioni sono un mezzo cruciale per la scienza per far fronte a sistemi che sono troppo difficili da studiare nella loro piena complessità. 

I dibattiti filosofici sull'idealizzazione si sono concentrati su due tipi generali di idealizzazioni: le cosiddette idealizzazioni aristoteliche e quelle galileiane. L'idealizzazione aristotelica equivale a “spogliare”, nella nostra immaginazione, tutte le proprietà di un oggetto concreto che riteniamo non pertinenti al problema in questione. Ciò consente agli scienziati di concentrarsi su un insieme limitato di proprietà isolate. Un esempio è un modello di meccanica classica del sistema planetario, che descrive la posizione di un oggetto in funzione del tempo e ignora tutte le altre proprietà dei pianeti.

Le idealizzazioni galileiane sono quelle che comportano distorsioni deliberate: i fisici costruiscono modelli costituiti da masse puntiformi che si muovono su piani privi di attrito; gli economisti presumono che gli agenti siano onniscienti; i biologi studiano popolazioni isolate; e così via. L'uso di semplificazioni di questo tipo ogni volta che una situazione è troppo difficile da affrontare era caratteristico dell'approccio di Galileo alla scienza. Un esempio di tale idealizzazione è un modello di movimento di un corpo ignorando la sua forma e grandezza e concentrando la sua massa in un punto. 

Le idealizzazioni galileiane e aristoteliche non si escludono a vicenda, e molti modelli mostrano entrambe in quanto sia tengono conto di un insieme ristretto di proprietà, sia le distorcono. 

Modelli fenomenologici - I modelli fenomenologici sono stati definiti in modi diversi, sebbene correlati. Una definizione comune li considera modelli che rappresentano solo proprietà osservabili dei loro sistemi di destinazione e si astengono dal postulare meccanismi per il momento nascosti e inaccessibili. Molti modelli fenomenologici, pur non essendo derivabili da una teoria, incorporano principi e leggi associati alle teorie. Il modello nucleare a goccia di liquido, ad esempio, fu ipotizzato nel 1939 da Niels Bohr e da John Wheeler per spiegare la perdita di massa durante una fissione nucleare. Esso descrive il nucleo come una goccia liquida e lo descrive come avente diverse proprietà originate da diverse teorie (idrodinamica ed elettrodinamica). La fissione del nucleo viene spiegata con l’analogia del processo di suddivisione di una goccia di liquido in due gocce più piccole. Alcuni aspetti di queste teorie, sebbene di solito non le teorie complete, vengono quindi utilizzati per determinare le proprietà sia statiche che dinamiche del nucleo. 

Infine, si è tentati di identificare i modelli fenomenologici con i modelli di un fenomeno. Qui, "fenomeno" è un termine generico che copre tutte le caratteristiche relativamente stabili e generali del mondo che sono interessanti da un punto di vista scientifico. L'indebolimento del suono in funzione della distanza dalla sorgente, il decadimento delle particelle alfa, le reazioni chimiche che avvengono quando un pezzo di calcare si dissolve in un acido, la crescita di una popolazione di conigli e la dipendenza dei prezzi delle case dal tasso base della Banca Europea sono fenomeni in questo senso.

Modelli esplorativi - I modelli esplorativi sono modelli che non vengono proposti in primo luogo per apprendere qualcosa su uno specifico sistema di destinazione o un particolare fenomeno stabilito sperimentalmente. I modelli esplorativi funzionano come punto di partenza di ulteriori esplorazioni in cui il modello viene modificato e perfezionato. Essi possono fornire prove di principio e suggerire possibili spiegazioni. Un esempio possono essere i primi modelli dell'ecologia teorica, come il modello Lotka-Volterra di interazione predatore-preda, che studia il comportamento qualitativo dell'accelerazione e del rallentamento della crescita della popolazione in un ambiente con risorse limitate. Tali modelli non forniscono un resoconto accurato del comportamento di una popolazione reale, ma forniscono il punto di partenza per lo sviluppo di modelli più realistici.

Strettamente correlata è anche la nozione di modello di sondaggio (o "modello di studio"). Modelli di questo tipo non svolgono una funzione rappresentativa e non ci si aspetta che ci informino su nulla al di là del modello stesso. Lo scopo di questi modelli è quello di testare nuovi strumenti teorici che vengono utilizzati in seguito per costruire modelli rappresentativi. Un falso modello può svolgere molte funzioni utili, perché ad esempio può aiutare a rispondere a domande su modelli più realistici, fornire un campo per rispondere a domande sulle proprietà di modelli più complessi, su fenomeni di esclusioni di variabili (factor out) che altrimenti non sarebbero visti, servire come caso limite di un modello più generale (due falsi modelli possono definire gli estremi di un continuum di casi su cui si suppone si trovi il caso reale, un po’ come il teorema del confronto in analisi, quello detto “dei due carabinieri”), o portare all'identificazione di variabili rilevanti e alla stima dei loro valori.

 

Modelli di dati - Un modello di dati è una versione corretta, rettificata, controllata e in molti casi idealizzata, dei dati che otteniamo dall'osservazione immediata, i cosiddetti dati grezzi. Tipicamente, prima si eliminano gli errori (ad esempio, si eliminano valori dal record che sono dovuti a un'osservazione errata) e poi si presentano i dati in modo "pulito", ad esempio disegnando una curva uniforme attraverso un insieme di punti. Questi due passaggi sono comunemente indicati come "riduzione dei dati" e "adattamento della curva". Quando indaghiamo, per esempio, la traiettoria di un certo pianeta, prima eliminiamo i punti che sono fallaci dai registri di osservazione e poi adattiamo una curva a quelli rimanenti. I modelli di dati giocano un ruolo cruciale nel confermare le teorie perché è il modello dei dati, e non i dati grezzi spesso disordinati e complessi, contro cui le teorie vengono testate.

La costruzione di un modello di dati può essere estremamente complicata. Richiede tecniche statistiche sofisticate e solleva serie questioni metodologiche. Come decidiamo quali punti del record devono essere rimossi? E, dato un insieme pulito di dati, quale curva ci adattiamo? Al centro di quest'ultima domanda c'è il cosiddetto problema dell'adattamento della curva, ovvero che i dati stessi non dettano né la forma della curva adattata né quali tecniche statistiche gli scienziati dovrebbero usare per costruire una curva. La raccolta, l'elaborazione, la diffusione, l'analisi, l'interpretazione e l'archiviazione dei dati sollevano molte questioni importanti al di là delle questioni relativamente ristrette relative ai modelli di dati. 

Modelli e conoscenza

Uno dei motivi principali per cui i modelli svolgono un ruolo così importante nella scienza è che svolgono una serie di funzioni cognitive. Ad esempio, i modelli sono veicoli per conoscere il mondo. Parti significative dell'indagine scientifica vengono svolte sui modelli piuttosto che sulla realtà stessa, perché studiando un modello possiamo scoprire caratteristiche e accertare fatti sul sistema che il modello rappresenta: i modelli consentono il "ragionamento surrogativo". Ad esempio, studiamo la natura dell'atomo di idrogeno, la dinamica di una popolazione o il comportamento di un polimero studiando i rispettivi modelli. Questa funzione cognitiva dei modelli è stata ampiamente riconosciuta in letteratura, e alcuni suggeriscono addirittura che i modelli diano origine a un nuovo stile di ragionamento, il “model-based reasoning”, secondo il quale si fanno inferenze mediante la creazione di modelli e la manipolazione, adattandole e valutandole.

L'apprendimento da un modello avviene in due momenti: nella costruzione e nella manipolazione. Non ci sono regole o ricette fisse per la costruzione del modello. Una volta che il modello è costruito, non apprendiamo le sue proprietà guardandolo; dobbiamo usare e manipolare il modello per carpirne i segreti. A seconda del tipo di modello con cui abbiamo a che fare, la costruzione e la manipolazione di un modello equivalgono a diverse attività che richiedono metodologie diverse.

I modelli materiali sembrano essere semplici perché sono utilizzati in contesti sperimentali comuni (ad esempio, mettiamo il modello di un'auto nella galleria del vento e misuriamo la sua resistenza all'aria). Quindi, per quanto riguarda l'apprendimento del modello, i modelli materiali non danno luogo a domande che vanno al di là di questioni riguardanti la sperimentazione più in generale.

Non così con i modelli immaginari e astratti. Quali sono i vincoli alla costruzione di modelli fittizi e astratti e come li manipoliamo? Una risposta naturale sembra essere che lo facciamo eseguendo un esperimento mentale (“E se fosse…”). Diversi autori hanno esplorato questa linea di argomentazione, ma hanno raggiunto conclusioni molto diverse e spesso contrastanti su come vengono eseguiti gli esperimenti mentali e quale sia lo stato dei loro risultati.

Un'importante classe di modelli è di natura computazionale. Per alcuni modelli è possibile derivare risultati o risolvere analiticamente equazioni di un modello matematico. Ma molto spesso non è così. È a questo punto che i computer hanno un grande impatto, perché ci permettono di risolvere problemi altrimenti intrattabili. Quindi, i metodi computazionali ci forniscono conoscenze su un modello in cui i metodi analitici rimangono silenziosi. Molte parti della ricerca attuale nelle scienze naturali e sociali si basano su simulazioni al computer, che aiutano gli scienziati a esplorare le conseguenze di modelli che non possono essere studiati altrimenti. La formazione e lo sviluppo di stelle e galassie, l'evoluzione della vita, lo sviluppo di un'economia, il comportamento morale e le conseguenze delle procedure decisionali in un'organizzazione sono esplorate con simulazioni al computer, per citare solo alcuni esempi.

Le simulazioni al computer possono suggerire nuove teorie, modelli e ipotesi, ad esempio, basati su un'esplorazione sistematica dello spazio dei parametri di un modello. Ma le simulazioni al computer comportano anche rischi metodologici. Ad esempio, possono fornire risultati fuorvianti perché, a causa della natura discreta dei calcoli effettuati su un computer digitale, consentono solo l'esplorazione di una parte dell'intero spazio dei parametri e questo sottospazio non è in grado di riflettere tutte le caratteristiche importanti del modello. La gravità di questo problema è in qualche modo mitigata dalla crescente potenza dei computer moderni. Ma la disponibilità di una maggiore potenza di calcolo può anche avere effetti negativi: può incoraggiare gli scienziati a elaborare rapidamente modelli sempre più complessi ma concettualmente prematuri, che implicano ipotesi o meccanismi poco compresi e troppi parametri regolabili aggiuntivi. Ciò può portare a un aumento dell'adeguatezza empirica, che può essere gradita per determinati compiti di previsione, ma non necessariamente a una migliore comprensione dei meccanismi sottostanti. Di conseguenza, l'uso delle simulazioni al computer può cambiare il peso che assegniamo ai vari obiettivi della scienza. Infine, la disponibilità della potenza del computer può indurre gli scienziati a fare calcoli che non hanno il grado di affidabilità che ci si aspetterebbe di avere. Ciò accade, ad esempio, quando i computer vengono utilizzati per estrapolare distribuzioni di probabilità in avanti nel tempo, il che può rivelarsi fuorviante. Quindi è importante non lasciarsi trasportare dai mezzi che offrono i nuovi potenti computer e perdere di vista gli obiettivi reali della ricerca. 

Una volta che abbiamo conoscenza del modello, questa conoscenza deve essere "tradotta" in conoscenza del sistema di destinazione. È a questo punto che la funzione rappresentativa dei modelli torna ad essere importante: se un modello rappresenta davvero qualcosa, allora può istruirci sulla realtà perché (almeno alcune) delle parti o aspetti del modello hanno parti o aspetti corrispondenti nel mondo. Ma se l'apprendimento è connesso alla rappresentazione e se ci sono diversi tipi di rappresentazioni (analogie, idealizzazioni, ecc.), allora ci sono anche diversi tipi di apprendimento. Se, ad esempio, abbiamo un modello che consideriamo una rappresentazione realistica, il trasferimento di conoscenza dal modello al sistema di destinazione avviene in modo diverso rispetto a quando abbiamo a che fare con un'analogia o un modello che implica ipotesi idealizzanti.

Secondo Ignazio Licata (2011), "Un modello teorico è un filtro cognitivo che rende conto di certe osservazioni e stabilisce una sorta di equilibrio tra l'osservatore e il mondo; è la forma generale del test per un insieme di domande che possiamo porre a una classe di fenomeni. Questo non significa che quelle domande siano uniche ed esaustive. Possiamo sempre provare a farne delle altre".

Alcuni modelli spiegano. Ma come possono assolvere a questa funzione dato che tipicamente implicano idealizzazioni? Questi modelli spiegano nonostante o a causa delle idealizzazioni che implicano? Un uso esplicativo dei modelli presuppone che essi rappresentino o possono anche spiegare modelli non rappresentativi? E che tipo di spiegazione forniscono i modelli?

C'è una lunga tradizione che richiede che l'insieme degli enunciati di una spiegazione scientifica debbano essere veri. Gli autori che operano in questa tradizione negano che le idealizzazioni diano un contributo positivo alla spiegazione ed esplorano come i modelli possono spiegare nonostante siano idealizzati. Le ipotesi idealizzate di un modello non fanno differenza per il fenomeno in esame e sono quindi irrilevanti a fini esplicativi. Al contrario, altri filosofi della scienza sostengono che i modelli che spiegano possono distorcere direttamente molte cause che fanno differenza.

Altri autori perseguono una linea opposta e sostengono che i falsi modelli spiegano non solo nonostante la loro falsità, ma di fatto a causa della loro falsità. Ad esempio, la filosofa della scienza Nancy Cartwright sostiene che "la verità non spiega molto" e suggerisce di spiegare un fenomeno costruendo un modello che si adatti al fenomeno nel quadro di base di una grande teoria. Per questo motivo, il modello stesso è la spiegazione che cerchiamo. 

La visione standard della spiegazione nella scienza è il modello a legge di copertura (covering-law model) proposto da Carl Gustav Hempel e Paul Oppenheim nell’articolo Studies in the Logic of Explanation del 1948, secondo cui lo spiegare un evento in riferimento ad un altro evento presuppone necessariamente un ricorso a leggi o proposizioni generali che mettano in correlazione eventi del tipo da spiegare (explananda) con eventi del tipo citato come sue cause o condizioni (explanantia). Esso presuppone che la conoscenza delle leggi sia alla base della nostra capacità di spiegare i fenomeni. Ma in realtà la maggior parte delle affermazioni di alto livello nella scienza sono generalizzazioni “ferme restando le altre condizioni”, che sono false a meno che non si verifichino determinate condizioni precise. La Cartwright fa esplicito riferimento a questo proposito al Paradosso di Simpson, che indica una situazione in cui una relazione tra due fenomeni appare modificata, o perfino invertita, dai dati in possesso, a causa di altri fenomeni non presi in considerazione nell'analisi (variabili nascoste). Ad esempio, in un gruppo con il 95% di vaccinati, le infezioni tra i vaccinati supererebbero quelle tra i non vaccinati semplicemente perché ci sono molte più persone vaccinate tra cui il virus può diffondersi. In un gruppo con il 20% di vaccinati in cui tutti siano esposti al virus, la maggior parte dei non vaccinati verrebbe infettata e la maggior parte dei vaccinati no. Tutto dipende dall’insieme di riferimento e da come viene scelto e illustrato. Bisogna essere molto cauti con le generalizzazioni ceteris paribus, altrimenti dati veri possono portare a conclusioni false. Si deve cercare un compromesso tra verità e potere esplicativo.

Molti hanno sottolineato che la comprensione è uno degli obiettivi centrali della scienza. In alcuni casi, vogliamo capire un certo fenomeno (ad esempio, perché il cielo è blu); in altri casi, vogliamo comprendere una teoria scientifica specifica (ad esempio la meccanica quantistica) che spiega un fenomeno in questione. A volte otteniamo la comprensione di un fenomeno comprendendo la teoria o il modello corrispondente. Ad esempio, la teoria dell'elettromagnetismo di Maxwell ci aiuta a capire perché il cielo è blu. È tuttavia controverso se la comprensione di un fenomeno presuppone sempre la comprensione della teoria corrispondente.

Ma perché i modelli giocano un ruolo così cruciale nella comprensione di un argomento? L’epistemologa Catherine Elgin sostiene che questo non avviene nonostante, ma proprio perché i modelli sono letteralmente falsi. Considera i falsi modelli come "falsità felici" che occupano il centro della scena nell'epistemologia della scienza e cita il modello del gas ideale in meccanica statistica e il principio di equilibrio di Hardy-Weinberg in genetica delle popolazioni come esempi di modelli letteralmente falsi che sono centrali nelle rispettive discipline. La comprensione è olistica e riguarda un argomento, una disciplina o un argomento, piuttosto che affermazioni o fatti isolati. 

Il geoide

Un geoide è una superficie perpendicolare in ogni punto alla direzione della verticale, cioè alla direzione della forza di gravità. Questa è la superficie che meglio descrive la superficie media degli oceani, quindi, la superficie media della Terra. Esso, infatti, è definibile come la superficie equipotenziale (in cui, cioè, il potenziale gravitazionale ha valore uguale) che presenta i minimi scostamenti dal livello medio del mare.

Non è possibile descrivere il geoide con una formula matematica risolvibile: per conoscere l'andamento del geoide, infatti, sarebbe necessario conoscere in ogni punto della superficie terrestre la direzione della forza di gravità, la quale a sua volta dipende dalla densità che la Terra assume in ogni punto, che a sua volta è funzione di numerosi fattori, come la natura e lo spessore delle rocce che costituiscono la crosta terrestre in una determinata area. Questo, tuttavia, è impossibile da conoscere senza una certa approssimazione, rendendo poco operativa dal punto di vista matematico la definizione di geoide.

 

Nell’immagine c’è la rappresentazione più aggiornata del geoide, ottenuta con misure di gravità satellitari. Le scale sono accentuate per far vedere il suo andamento: in realtà esso si discosta assai poco dall’ellissoide di rotazione al quale si approssima la forma della Terra. Si tratta di un modello volutamente sbagliato, ma solo così ha funzione esplicativa. A seconda della loro funzione, i modelli scientifici si discostano spesso dal sistema di destinazione: non è affatto vero che una rappresentazione debba essere la più vicina possibile alla realtà. Certe volte si spiega meglio distorcendo i dati reali. 

Modelli e teoria

Una questione importante riguarda la relazione tra modelli e teorie. C'è uno spettro completo di posizioni che vanno dai modelli subordinati alle teorie ai modelli indipendenti dalle teorie.

Modelli come sussidiari alla teoria - Per discutere la relazione tra modelli e teorie nella scienza è utile ricapitolare brevemente le nozioni di un modello e di una teoria in logica. Una teoria è considerata un insieme (di solito deduttivamente chiuso) di frasi in un linguaggio formale. Un modello è una struttura che rende vere tutte le frasi di una teoria quando i suoi simboli sono interpretati come riferiti a oggetti, relazioni o funzioni di una struttura. La struttura è un modello della teoria nel senso che è correttamente descritta dalla teoria. I modelli logici sono talvolta indicati anche come "modelli di teoria" per indicare che sono interpretazioni di un sistema formale astratto.

I modelli nella scienza a volte riportano dalla logica l'idea di essere l'interpretazione di un calcolo astratto. Questo è saliente in fisica, dove le leggi generali (come l'equazione del moto di Newton) sono al centro di una teoria. Queste leggi sono applicate a un particolare sistema, ad esempio a un pendolo, scegliendo una funzione di forza speciale, facendo ipotesi sulla distribuzione di massa del pendolo, ecc. Il modello risultante è quindi un'interpretazione (o realizzazione) della legge generale.

È importante mantenere separate le nozioni di un modello logico e di un modello rappresentativo: si tratta di concetti distinti. Qualcosa può essere un modello logico senza essere un modello rappresentativo e viceversa. Questo, tuttavia, non significa che qualcosa non possa essere un modello in entrambi i sensi contemporaneamente. Infatti, molti modelli nella scienza sono sia modelli logici che rappresentativi. Il modello di Newton del moto planetario è un esempio calzante: il modello, costituito da due sfere perfette omogenee situate in uno spazio altrimenti vuoto che si attraggono gravitazionalmente, è contemporaneamente un modello logico (perché rende veri gli assiomi della meccanica newtoniana quando sono interpretati come riferiti al modello) e un modello rappresentativo (perché rappresenta il Sole e la Terra reali).

Modelli indipendenti dalle teorie - L’idea che i modelli siano subordinati alla teoria e non svolgono alcun ruolo al di fuori del contesto di una teoria è stata messa in discussione in diversi modi, con gli autori che sottolineano che i modelli godono di vari gradi di libertà dalla teoria e funzionano autonomamente in molti contesti. L'indipendenza può assumere molte forme e gran parte della letteratura sui modelli si occupa di indagare varie forme di indipendenza.

Modelli come completamente indipendenti dalla teoria. L'allontanamento più radicale da un'analisi dei modelli centrata sulla teoria è la realizzazione che ci sono modelli che sono completamente indipendenti da qualsiasi teoria. Un esempio di tale modello è il modello prede-predatori di Lotka-Volterra. Il modello è stato costruito utilizzando solo ipotesi relativamente comuni su predatori e prede e la matematica delle equazioni differenziali. Non c'era appello a una teoria delle interazioni predatore-preda o a una teoria della crescita della popolazione, e il modello è indipendente dalle teorie sul suo argomento. Se un modello è costruito in un dominio in cui non è disponibile alcuna teoria, allora il modello viene talvolta definito "modello sostitutivo", perché il modello sostituisce una teoria.

Modelli come complementi di teorie. Una teoria può essere specificata in modo incompleto nel senso che impone solo alcuni vincoli generali, ma tace sui dettagli delle situazioni concrete, che sono fornite da un modello. Le teorie possono essere troppo complicate da gestire. In questi casi un modello può integrare una teoria fornendo una versione semplificata dello scenario teorico che consente una soluzione. Per aggirare questa difficoltà, i fisici costruiscono modelli fenomenologici trattabili, come il MIT General Circulation Model, che è un modello numerico, il quale utilizza il metodo dei volumi finiti nell'integrazione computerizzata delle equazioni differenziali alle derivate parziali che governano la circolazione nell'oceano e nell'atmosfera terrestre. Essi descrivono efficacemente i gradi rilevanti di libertà del sistema in esame. Il vantaggio di questi modelli è che producono risultati in cui le teorie rimangono mute. Il loro svantaggio è che spesso non è chiaro come comprendere la relazione tra il modello e la teoria, poiché i due sono, in senso stretto, contraddittori.

Modelli interpretativi. Nancy Cartwright sostiene che i modelli non solo aiutano l'applicazione di teorie che sono in qualche modo incomplete; sostiene che i modelli sono coinvolti anche ogni volta che viene applicata una teoria con una struttura matematica generale. Le principali teorie della fisica (meccanica classica, elettrodinamica, meccanica quantistica e così via) sono formulate in termini di concetti astratti che devono essere concretizzati affinché la teoria fornisca una descrizione del sistema di destinazione. Ad esempio, quando si applica la meccanica classica, il concetto astratto di forza deve essere sostituito con una forza concreta come la gravità. Per ottenere equazioni trattabili, questa procedura deve essere applicata a uno scenario semplificato, ad esempio quello di due pianeti perfettamente sferici e omogenei in uno spazio altrimenti vuoto, piuttosto che alla realtà nella sua piena complessità. Il risultato è un modello interpretativo, che fonda l'applicazione di teorie matematiche a obiettivi del mondo reale. Tali modelli sono indipendenti dalla teoria in quanto la teoria non determina la loro forma, eppure sono necessari per l'applicazione della teoria a un problema concreto.

Modelli come mediatori. La relazione tra modelli e teorie può essere complicata e disordinata. I modelli sono "agenti autonomi" in quanto sono indipendenti sia dalle teorie che dai loro sistemi di destinazione, ed è questa indipendenza che consente loro di mediare tra i due. Le teorie non ci forniscono algoritmi per la costruzione di un modello; non sono "distributori automatici" in cui si può inserire un problema e un modello salta fuori. La costruzione di un modello richiede spesso una conoscenza dettagliata dei materiali, degli schemi di approssimazione e dell'impostazione, e questi non sono forniti dalla teoria corrispondente. Inoltre, il funzionamento interno di un modello è spesso guidato da una serie di teorie diverse che lavorano in modo cooperativo. Nella modellazione climatica contemporanea, ad esempio, elementi di diverse teorie (fluidodinamica, termodinamica, elettromagnetismo, ecc.) sono messi in opera in modo cooperativo. Ciò che fornisce i risultati non è l'applicazione rigorosa di una teoria, ma le voci di diverse teorie quando vengono utilizzate in coro l'una con l'altra in un unico modello.

 -.-.-.-

La fonte principale di questo articolo è la voce Models in Science, coordinata da Roman Frigg (London School of Economics) e Stephen Hartmann (Leibniz-Rechenzentrum der Bayerischen Akademie der Wissenschaften, Monaco di Baviera), della Stanford Encyclopedia of Philosophy, consultata tra l’ottobre e il novembre 2021. Poi ci ho anche messo del mio, ovviamente.